Нахождение точки пересечения двух линий по углам и известным точкам (биангуляция)
по адресу http://gis-lab.info/qa/biangulation.html
Немного простейшей геометрии для решения задачи биангуляции. Применение в орнитологии
Задача
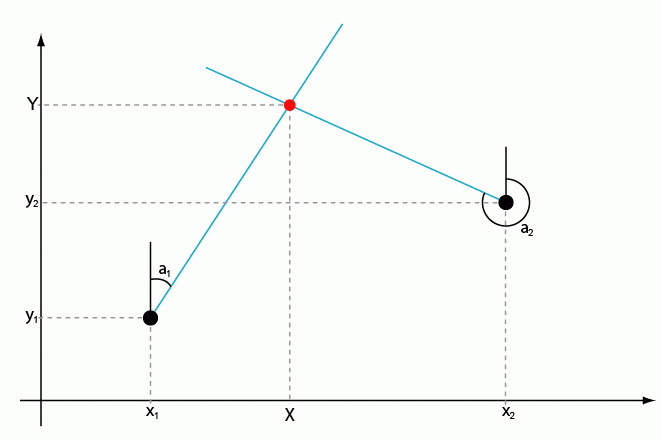
Найти точку пересечения двух прямых отложенных от двух точек с известными координатами и азимутов от этих точек.
Применение
Для изучения поведения животных часто используют радиотелеметрический метод: исследуемый объект помечается радиопередатчиком, который испускает радиосигнал определенной частоты и далее исследователь при помощи приемника и принимающей антенны следит за перемещениями этого объекта. Одним из возможных способов определения точного местоположения объекта является метод биангуляции. Для этого исследователю требуется взять 2 азимута на исследуемый объект с точек с известными координатами. Местоположение объекта будет соответствовать точке пересечения этих двух азимутов. Координаты точек, с которых засекаются азимуты можно снять с помощью спутникового навигатора (GPS), либо азимуты снимаются с реперных точек, координаты которых известны заранее. Азимут в этом случае – направление на источник наиболее сильного сигнала, исходящего от меченного передатчиком объекта, измеряемое обычно в градусах.


Перед расчетами необходимо точки полученные с помощью GPS перевести в спроецированную систему координат, например соответствующую зону UTM, это можно сделать с помощью DNRGarmin.
Для того чтобы рассчитанное местоположение исследуемого объекта наиболее точно соответствовало реальному положению нужно учитывать следующее:
1) необходимо стараться дождаться момента, чтобы ошибка определения координат в навигаторе была как можно меньше.
2) чтобы угол между азимутами стремился к 90 градусам (по крайней мере, был больше 30 и меньше 150 градусов).
Расстояние, с которого следует снимать азимут, зависит от дальности действия передатчика, при этом применяется эмпирическое правило, что погрешность в определении азимута увеличивается на 1 метр с удалением от исследуемого объекта на каждые 10 м. Т.о. при снятии азимута с расстоянием до объекта 100 м погрешность составит 10 м. Однако, это правило применимо на ровной открытой местности. Следует учитывать, что неровности рельефа и древесно-кустарниковая растительность экранируют и отражают сигнал. Следует избегать нахождения в непосредственной близости от исследуемого объекта, т.к. во-первых, слишком сильный сигнал затруднит определение точного азимута, а, во-вторых, в некоторых случаях будет невозможно рассчитать точку пересечения из-за того, что второй азимут будет проходить за точкой снятия первого азимута. Временной интервал между снятием пары азимутов должен быть минимизирован, но, конечно, зависит от подвижности исследуемого животного.
Решение
Задача решается с помощью простейшей геометрии и решения системы уравнений.
Для начала из точки и азимута получаем уравнение прямой, для этого:
Из уравнения общего вида:
ax + by + c = 0
при условии, что b<>0 получаем
y = kx + d, где k=-(a/b), d=-(c/b)
таким образом, получаем
k=tan(a)
d=y-tan(a)*x
b=1
Далее решив систему уравнений:
k1x + d1 = y
k2x + d2 = y
Получаем координаты X и Y общей точки двух прямых (точки пересечения).
В уравнении необходимо предусмотреть два особых случая, когда прямые параллельны (k1=k2).
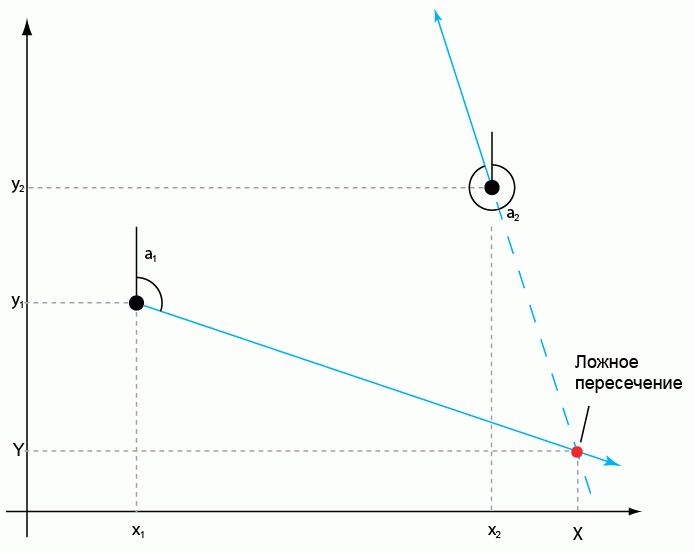
Так как мы имеем дело не с векторами и не с лучами, то есть у линий нет начала и конца, то так же необходимо предусмотреть случай пересечения прямых вне области интереса, т.н. ложное пересечение. Решение этой задачи достигается измерением азимута из ложной точки a3 на точку 2, если азимут a3 = a2, то пересечение ложное, обратный азимут от полученной точки обратно на исходные 2 не должен быть равен одному из исходных азимутов.
Необходимая процедура на языке Avenue выглядит так:
a1rad = (90-a1)*pi/180
a2rad = (90-a2)*pi/180 'в случае если линия параллельна оси абсцисс
if ((a1 = 0) or (a1 = 180)) then
l1a = 1
l1b = 0
l1c = x1
else
l1a = -(a1rad.tan)
l1b = 1
l1c = y1 - (a1rad.tan*x1)
end
if ((a2 = 0) or (a2 = 180)) then
l2a = 1
l2b = 0
l2c = x2
else
l2a = -(a2rad.tan)
l2b = 1
l2c = y2 - (a2rad.tan*x2)
end
D1 = l1a*l2b
D2 = l2a*l1b
D3 = D1 - D2
'Если линии параллельны, в поле результата записываются несуществующие значения
if (D3 = 0) then
resX = 9999
resY = 9999
else resX = ((l1c*l2b) - (l2c*l1b))/D3
resY = ((l1a*l2c) - (l2a*l1c))/D3 end
Здесь находится расширение для Arcview GIS для расчета точек пересечения двух прямых, включая проверку ложных пересечений.
В качестве исходных данных для работы используется точечная тема Arcview (в формате shape или заданная как Event theme таблица). Тема должна быть выделена (активна). Пары исходных координат (засечек) в таблице должны располагаться друг за другом.
Названия полей должны быть следующими:
X - долгота
Y - широта
Bear - азимут (угол от оси Y по часовой стрелке)
(скрипт легко модифицируется если у вас другие названия полей).
В названиях полей не должно содержаться символа #. Такие поля следует переименовать. Покрытия Arcinfo некоторые поля которых как правило содержат такой символ нужно сконвертировать в shape-файл и также переименовать поля, убрав #.
Результатом работы скрипта является shape-файл в атрибутивной таблице которого будут находится расчетные координаты точки пересечения для каждой пары засечек. Полей в исходной таблице может быть больше чем 3 (x, y, bear), дополнительные поля перенесутся в результирующую тему. Они будут заполнятся значениями из первой точки пары из исходной таблицы.
Ссылки по теме