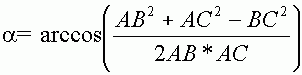Вычисление азимута и угла между двумя прямыми для прямоугольных координат
по адресу http://gis-lab.info/qa/aveazimuth.html
Немного геометрии для решения задачи нахождения азимута, используемый код может применяться в других расширениях.
<right>спасибо Алексею Таченкову за помощь с геометрией</right>
Вычисление азимута
Азимут - взятый из одной точки на другую - есть угол отклонения прямой, полученной соединением двух данных точек (А и B), от прямой проведенной на север из точки номер один, угол считается по часовой стрелке.
A {X1,Y1}
B {X2,Y2}
C {X1,Y2}
Расстояние между двумя точками:
Исходя из теоремы косинусов и теоремы Пифагора:
BC2 = AB2+AC2 - 2AB*AC*cos(бета)
AB2 = AC2+BC2 (так как треугольник прямоугольный)
бета = arccos(AC/AB)
Существует 4 возможных варианта зависящих от взаимного расположения точек A и B, в данном примере мы определяем азимут от точки А на точку B, dX = X1 - X2, dY = Y1 - Y2:
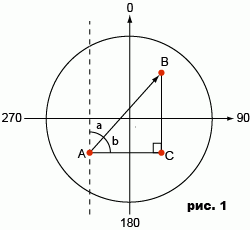
1. Точка B находится выше и правее точки А, dX < 0, dY < 0 (рис.1).
Азимут (альфа) = 90-бета
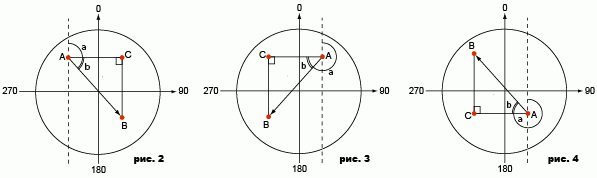
2. Точка B находится ниже и правее точки А,dX < 0, dY > 0 (рис. 2)
Азимут (альфа) = 90+бета
3. Точка B находится ниже и левее точки A, dX > 0, dY > 0 (рис. 3)
Азимут (альфа) = 270-бета
4. Точка B находится выше и левее точки A, dX > 0, dY < 0 (рис. 4)
Азимут (альфа) = 270+бета
Вычислениям приведенным выше соответствует следующий код на языке Avenue (pt2 - точка А, pt1 - точка B):
dX = pt2.getx - pt1.getx
dY = pt2.gety - pt1.gety
dist = ((dX*dX) + (dY*dY)).sqrt
dXa = dX.abs
beta = (dXa / dist).ACos.AsDegrees
if (dX > 0) then
if (dY < 0) then
angle = 270 + beta
else
angle = 270 - beta
end
else
if (dY < 0) then
angle = 90 - beta
else
angle = 90 + beta
end
end
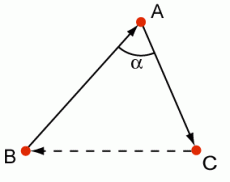
Вычисление угла между двумя прямыми (тремя точками)
Из теоремы косинусов:
На Avenue:
ab = a.distance(b) bc = b.distance(c) ac = a.distance(c) alpha = (((ab^2)+(ac^2) - (bc^2))/(2*ab*ac)).ACos.AsDegrees