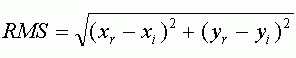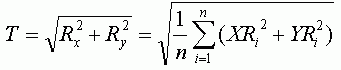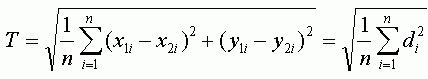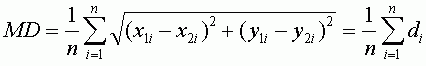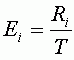Среднеквадратичная ошибка (RMSE)

Эта страница опубликована в основном списке статей сайта
по адресу http://gis-lab.info/qa/rmse.html

Краткая объяснение что такое RMSE применительно к данным ДЗЗ

Среднеквадратичная ошибка (Root Mean Square Error, RMS Error, RMSE) - расстояние между двумя точками.

В случае если речь идет о привязке данных, в качестве точек между которыми измеряется расстояние могут выступать:

1. Исходная точка и конечная точки (например результат трансформации), в этом случае RMSE будет показателем насколько исходная точка близка к конечной - текущая ошибка.
2. Желаемое положение выходной точки (точка поставленная пользователем) и результатом ее трансформации (точка поставленная моделью). Трансформация - то или иное математическое преобразование исходных координат в конечные, примером такого преобразования может быть аффинная или полиномиальная трансформация. В данном случае RMSE показывает насколько используемая трансформация позволяет точно приблизить исходную точку к конечной, т.е. RMSE в этом случае - ошибка трансформации.

Как видно на иллюстрации ниже, выходные точки 1, 2, 3 поставленные оператором (синие) совпадают с трансформированными (расчетными) значениями (зеленые) и не видны из-за точного совпадения, а вот точка 4 поставлена не там, куда бы она попала используя ту же трансформацию, это дает возможность вычислить для нее RMSE, для точек 1, 2, 3 RMSE = 0.

Привязываемое изображение слева, изображение используемое в качестве источника координат (привязанное) справа.

Примечание: здесь и далее в статье, как и в ERDAS IMAGINE Field Guide, RMS определяется как расстояние (длина гипотенузы), что не совсем соответствует определению Root Mean Squared, так как отсутствует компонент усреднения, классический RMS должен вычисляться делением выражения под корнем на N измерений, в этом случае на 2. В данном случае удобнее называть RMS - расстоянием.

Ошибка RMS рассчитывается по следующей формуле, представляющей из себя формулу вычисления расстояния:

где x_i, y_i - исходные координаты, x_r, y_r - конечные координаты

RMSE выражается как расстояние в единицах исходной системы координат, то есть, если вы привязываете только что отсканированную карту, то RMSE будет выражаться в пикселях (или долях пикселя), если вы производите дополнительную привязку снимка, то RMSE будет показывать значения в метрах. Значение RMSE равное 2 для определенной точки будет означать, что ее исходная координата удалена на 2 пикселя или метра от конечной (расчетной) точки.

Чтобы лучше понять когда и как можно получить RMSE при привязке можно использовать следующий алгоритм, иллюстрирующую процесс привязки с помощью аффинного преобразования:

1. Получение изображения, например сканированием, изображение получает пиксельную систему координат X,Y (колонка, ряд).
2. Расстановка трех точек с начальными и конечными координатами. Эти координаты указывают:
   • Начальные координаты - положение точки на непривязанном материале (координаты конкретного пиксела по системе ряд/колонка);
   • Конечные координаты - положение точки на привязанном материале, любом источнике координат, географических или спроектированных.
3. Три точки - минимальное количество, необходимое для того, чтобы решить систему уравнений аффинного преобразования:
   x₀ = a+ b*x + c*y
   y₀ = d + e*x + f*y Решение уравнения заключается в нахождении всех шести коэффициентов, например решением системы уравнений:
   x1' = a + b*x1 + c*y1
   y1' = d + e*x1 + f*y1
   x2' = a + b*x2 + c*y2
   y2' = d + e*x2 + f*y2
   x3' = a + b*x3 + c*y3
   y3' = d + e*x3 + f*y3 Если точек меньше чем минимально необходимо - решить систему невозможно, нельзя найти коэффициенты трансформации и соответственно невозможно произвести пересчет координат. RMSE для точек также вычислить невозможно.
4. Расстановка минимально необходимого количества точек для данного преобразования (трех) приводит к тому, что RMSE для каждой точки становится равна 0. Можно производить трансформацию. Однако в таком случае мы не можем сделать выводов о качестве точек, ведь для этого надо рассчитать RMSE, а значит....
5. Ставим дополнительные точки. Появление новых данных как правило приводит к тому, что то положение, куда мы ставим конечную точку в процессе привязки и ее расчетное положение не совпадают. Это делает возможным расчет RMS ошибки.
   

С примером и математикой расчета полиномиального преобразования 2-ой степени можно прочитать в статье "Полиномиальные преобразования - вычисления и практика".

Помимо RMSE часто также можно увидеть также значения ошибки по одной из осей X или Y. Эти значения являются остатками (residuals) и могут быть рассчитаны для каждой точки. Изучение значений этих ошибок может помочь понять, почему привязанный материал смещен по одной из осей. Это проблема часто возникает при привязке данных полученных при съемке под углом (не в надир).

Уравнение вычисления RMS для каждой точки можно переписать как:

где XR и YR - остаточные ошибки по X и Y соответственно.

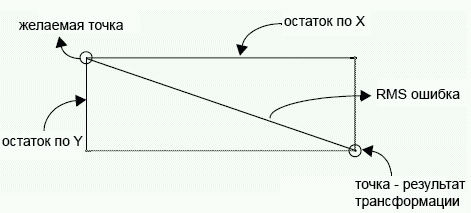
Графически ошибки по X и Y, а также RMSE соотносятся следующим образом:

Вычислив RMSE для каждой точки, можно также определить общую ошибку по X (Rx), Y (Ry) и общую RMSE (T) используя следующие формулы:

где n - число контрольных точек, i - порядковый номер контрольной точки, d - расстояние между парой точек.

Связь со средним расстоянием

Другим, достаточно объективным, способом оценить точность привязки является среднее расстояние, которое очень похоже по формуле на RMSE, но является менее консервативным показателем, так как расстояния не возводятся в квадрат как в RMSE. Выразив расстояние через d, приведем для сравнения формулы вычисления общей RMSE (T) и среднего расстояния (MD):

RMSE является более общеупотребимым в литературе.

Другим распространенным способом описания точности набора измерений являются квантили дробные стандартному отклонению (сигма).

Вклад точки в общую RMSE

Для того, чтобы вычислить вклад точки в общую ошибку (E_i), необходимо разделить RMSE этой точки (R_i) на общую RMSE.

Допуск RMSE

В большинстве случаев, вместо того, чтобы усложнять тип трансформации (например переходить к более высоким порядкам полиномиальных преобразований) имеет смысл допустить некоторую ошибку. Величину допустимой RMSE можно представить как окно, окружающее точку с желаемыми координатами, положением расчетной точки внутри которого считается корректным. Например, если допуск RMSE равен 2, то расчетный пиксел может находится в двух пикселях от указанного оператором и являться допустимым. Величина допустимой ошибки зависит от типа и точности данных, задачи и точности контрольных точек.

Важно помнить, что RMSE указывается в пикселях, поэтому, если привязываются данные Landsat имеющие разрешение 30 метров и задача осуществить привязку с точностью не меньше тех же 30 метров, то RMSE не должна превышать 1.00 (пикселя).

Оценка RMSE

Если RMSE расчитана и найдена слишком высокой, есть 4 варианта решения проблемы:

1. Найти и удалить контрольные точки с большой RMSE, подразумевая, что это наименее точные точки. Это чревато еще возникновением еще больших ошибок, если отбраковываемая точка - единственная на большой участок изображения.
2. Увеличить допуск RMSE.
3. Увеличить сложность функции трансформации, которая более точно будет соответствовать введенным точкам. RMSE точек при этом уменьшится, однако использование сложных криволинейных функций может привести к нежелательным сильным искажениям растра.
4. Оставить только точки в которых Вы уверены, что они правильны.

В статье использованы материалы ERDAS IMAGINE Field Guide

Ссылки по теме

• Полиномиальные преобразования
• Полиномиальные преобразования - вычисления и практика