Сравнение разных способов вычисления длин и азимутов
по адресу http://gis-lab.info/qa/diff-calc.html
Измерить расстояние и азимут между двумя точками можно несколькими разными способами. Эта статья иллюстрирует порядок разницы между разными способами вычисления.
Несмотря на кажуюся простоту, операция расчета длины линии соединяющей две точки и азимута из одной точки на другую может приводить к достаточно сильно отличающимся результатам в зависимости от того, как производится это измерение. Перед осуществлением этих измерений следует четко определить, какое именно расстояние/азимут нужно вычислить и для чего.
Измерение расстояния может осуществляться одним из следующих методов:
- Геодезические координаты, расстояние - длина дуги большого круга проходящего через две точки (подробнее). Длина дуги большого круга может быть рассчитана для двух случаев:
- Случай сферы
- Случай эллипсоида
- Прямоугольные координаты или геодезические координаты, расстояние длина прямой линии соединяющей две точки (подробнее)
- Частный случай, длина линии румба (локсодромное расстояние) - вычисляется в проекции Меркатора, в которой, все прямые линии - линии румба (пересекают параллели под постоянным углом)
- Измерения в других проекциях - длины линий соединяющих две точки будут различны для разных проекций. Проекции имеющей постоянный масштаб длин для любых направлений - не существует в природе.
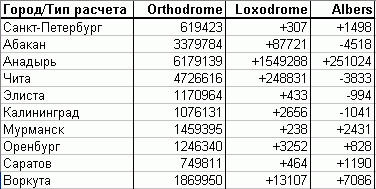
Для того, чтобы получить практическое представление о порядке разницы измерений проведенных различными способами, можно воспользоваться следующей таблицей. В ней приведены расчеты расстояния между аэропортами Москвы (Шереметьево) и других городов России (источник данных о положении объектов ). Orthodrome - длина дуги большого круга (кратчайшее расстояние) на сфере, Loxodrome - длина линии румба, Albers - расстояние между точками в проекции Albers Equal Area (параметры - Siberia). Расстояния Loxodrome и Albers даны как относительные расстояния Orthodrome.
Как видно из таблицы, локсодромное расстояние никогда не превышает ортодромное, а значения для спроектированных данных достаточно сильно отличаются от измерений на сфере. Так как Москва и Мурманск находятся на практически одной долготе, разница между длиной дуги большого круга и линией румба минимальна, так как меридианы являются одновременно и большими кругами и линиями румба (0o).
Измерение азимута из первой точки на вторую также может осуществляться по разному:
- Геодезические координаты, начальный (ортодромный) азимут - угол при старте из первой точки и движению по кратчайшему расстоянию, конечной точкой является вторая точка. Начальный азимут не постоянен по ходу движения (подробнее).
- Геодезические координаты, постоянный (локсодромный) азимут - постоянный угол, следуя которому можно попасть из первой точки во вторую. Расстояние между двумя точками при этом не является кратчайшим (подробнее).
- Прямоугольные координаты, в большинстве случаев - азимут - направление от одной точки на другую (север - 0) (подробнее).
- Частный случай: постоянный (локсодромный) азимут в случае использовании проекции Меркатора (результаты расчета идентичны варианту 2)
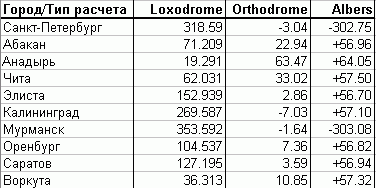
Для того, чтобы получить практическое представление о порядке разницы измерений проведенных различными способами, можно воспользоваться следующей таблицей. В ней приведены расчеты расстояния между аэропортами Москвы (Шереметьево) и других городов России (источник данных о положении объектов) Loxodrome - постоянный азимут, Orthodrome - начальный азимут, Albers - азимут в проекции Albers Equal Area (параметры - Siberia). Азимуты Orthodrome и Albers даны как относительные азимута Loxodrome.
Как видно из таблицы, в зависимости от используемого расчета, результаты могут сильно отличаться от значения постоянного (локсодромного) азимута. К особенно сильно отличающимся значениям приводит использование для расчетов спроектированных данных. Так как Москва и Мурманск находятся на практически одной долготе, разница между ортодромным и локсодромным азимутом минимальна, так как меридианы являются одновременно и большими кругами и линиями румба (0o).