Расчёт фрактальной размерности Минковского для векторных объектов в QGIS
Фрактальная размерность Минковского, применение подобных фрактальных размерностей в географии, описание QGIS модуля для расчета размерности Минковского для векторных объектов.
В географических исследованиях время от времени обращаются к оценке фрактальных размерностей изучаемых объектов, предпринимаются попытки интерпретировать различные значения этих фрактальных размерностей, сравнивать их между собой. В этой статье кратко рассмотрена сущность размерности Минковского, приведены примеры применения фрактальных размерностей в географии, а также представлен простой QGIS-модуль, позволяющий произвести оценку размерности Минковского для объектов из любого набора линейных векторных геоданных.
Фрактальная размерность Минковского
Примеры применения фрактальных размерностей в географии
Вместе с развитием теоретических основ фрактальной геометрии естественным образом возникали попытки их применения в естественных науках - геологии, географии, биологии и других. Сегодня можно найти немало статей и даже больших книг [2,3], посвященных различным аспектам географической интерпретации фракталов.
В урбанистике исследователи часто пытаются связать различные аспекты городского пространства с фрактальной размерностью контуров города и её изменениями во времени. Вот, к примеру, фрактальная размерность крупных городов мира [4]:
Авторы оценивают фрактальные размерности в совокупности с большим набором социально-экономических показателей развития города, таких как ИРЧП, обеспеченность населения автотранспортом, динамика численности населения и других.
Множество работ в области урбанистики посвящено фрактальным исследованиям транспортных сетей [5], границ городов, в том числе и с использованием размерности Минковского [6], и других аспектов [7].
Широкий интерес к фракталам обнаруживается и в области гидрологии. Оценка фрактальных характеристик речных систем позволяет расширить понимание их генезиса и спрогнозировать дальнейшую динамику развития, а также оценить взаимосвязь различных геометрических и гидродинамических параметров рек [8, 9, 10, 11].
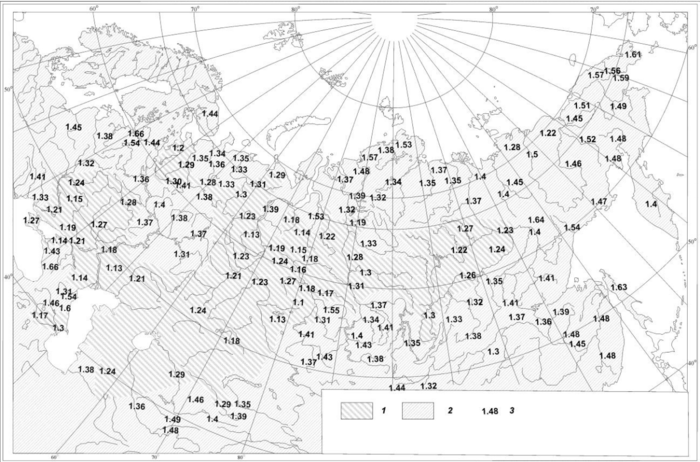
На этой карте отображено распределение величины фрактальной размерности речных систем по территории Северной Евразии [12]
Автор отмечает связь между фрактальной размерностью и высотой речного водосбора, глубиной вреза речной сети, а также с увлажненностью территории.
Подобные исследования можно найти в решениях задач ландшафтоведения [13], геоботаники [14], физической географии [15], экологии [16] и многих других.
QGIS-модуль для вычисления размерности Минковского
Общая информация
Разработанный простой модуль позволяет вычислить размерность Минковского для объектов из наборов векторных геоданных с линейным типом геометрии. Не требует дополнительных библиотек, распространяется по лицензии GNU GPL v2, поддерживается версиями QGIS от 2.0 и выше.
Для установки модуля достаточно загрузить архив и распаковать его содержимое как директорию в <home dir>/.qgis2/python/plugns/
Например, в Windows это может быть папка C:/users/silent/.qgis2/python/plugins/minkowskiDimCalculator/
В Linux: /home/silent/.qgis2/python/plugins/minkowskiDimCalculator/
Описание
Основным результатом работы модуля является создание нового (или перезапись существующего) атрибута векторного слоя с записью в него для каждого объекта его фрактальной размерности. Пользователь выбирает исследуемый векторный слой, а также задаёт имя атрибута, в который будет записан результат. Далее, в зависимости от выбранного подхода построения сетки, задаёт параметры.
Модуль поддерживает два подхода к построению сеток для вычисления фрактальной размерности: Layer Grid и Feature Grid.
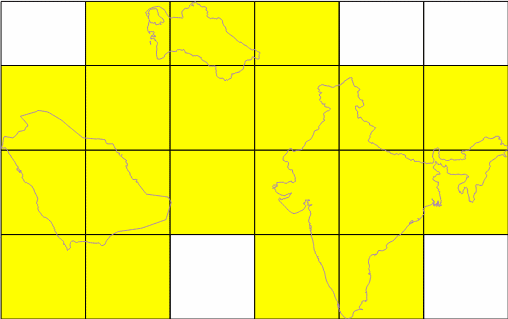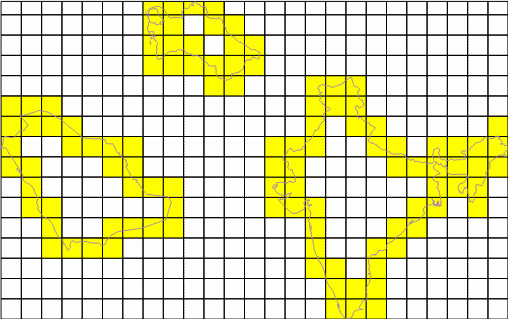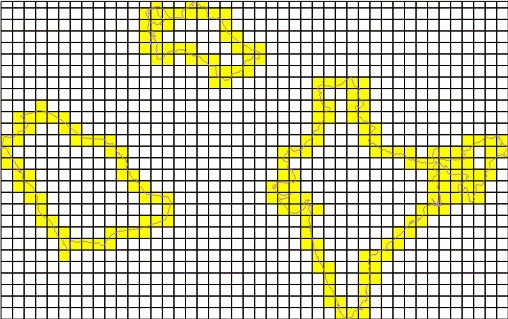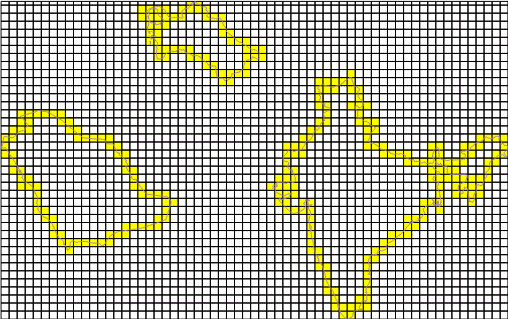
Метод Layer Grid подразумевает построение единой сетки на всю исследуемую территорию (фактически, охват сетки совпадет с охватом слоя или выделенных объектов), и одновременный расчет необходимых показателей для всех объектов по ней. При этом параметры сетки (начальный и конечный размер, количество шагов) задаются пользователем один раз.
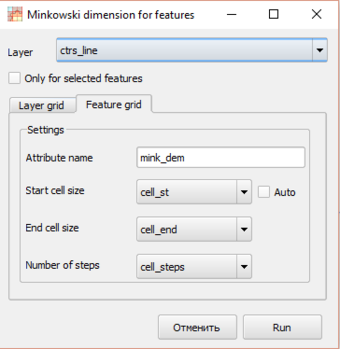
Метод Feature Grid подразумевает построение отдельных сеток для каждого отдельного объекта, с возможностью задания параметров сетки через атрибуты каждого объекта.
При обоих способах возможен автоматический подбор параметров, на данном этапе реализованный довольно примитивно (основанный на охвате наибольшего объекта слоя).
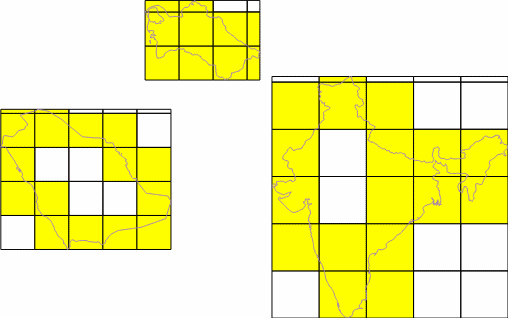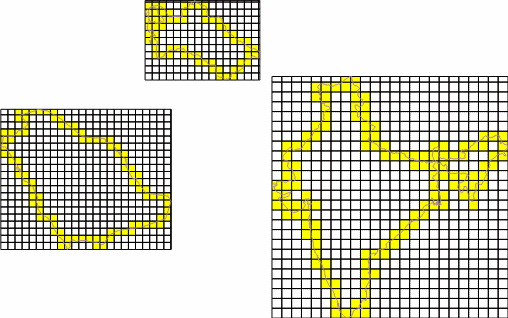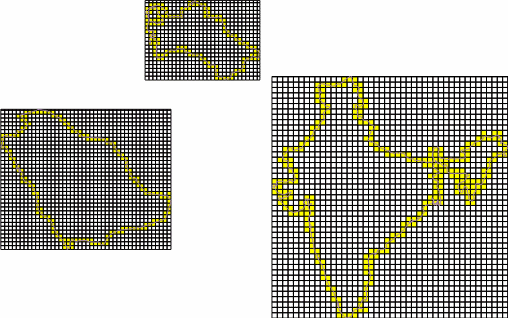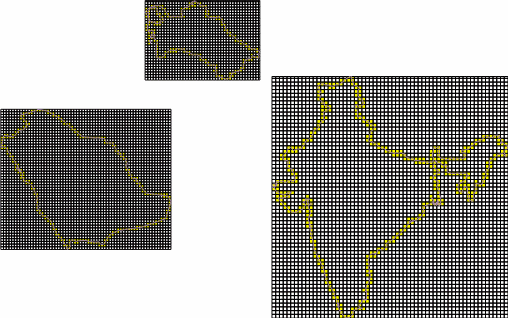
Примеры использования и комментарий
Литература
1.
2. Nina Siu-Ngan Lam, Lee De Cola. Fractals in Geography, 2002. 308p.
3. André Dauphiné. Fractal Geography, 2012. 241p.
4. Gizem Erdogan, K. Mert Cubukcu. Explaining fractal dimension in populous cities, EURAU 2014
9. Никора В.И. Фрактальные свойства некоторых гидрологических объектов. Кишинев: ИГИГ АН МССР, 1988. 43 с
11. Shi-Xia Z., Zi-Wen W., Shi-Min Z., & Zu-Hong Y. (2014). Research on the relevance between flood disaster and fractal characteristics of river networks-a case study of Hangzhou, China. Disaster Advances, 7(5), 94-100
12. А.Ю. Сидорчук. Фрактальная геометрия речных сетей. Геоморфология. 2014;(1):3-14
15. Gao J., & Xia Z.-G. Fractals in physical geography. Progress in Physical Geography, 20(2), 178-191