Моделирование проекций орбит ИСЗ на поверхность Земли на Python с использованием модели SGP4 и API space-track.org
Определение положения ИСЗ по орбитальным данным на заданное время по модели SGP4. Автоматизированное получение орбитальных данных с помощью API сервиса space-track.org. Пример реализации на языке Python.
Задачу определения положения того или иного искусственного спутника Земли в заданный момент времени (в прошлом или недалёком будущем) приходится решать для самых разнообразных целей, в том числе связанных с дистанционным зондированием Земли из космоса. Часть данных (например, многие продукты MODIS) распространяется без строгой географической привязки, а лишь с указанием времени непосредственного наблюдения территории для каждой сцены, — и для автоматизации поиска и загрузки таких данных требуется вычислять время пролёта спутника над исследуемыми объектами. Часто возникает и потребность определить время зондирования заданной территории в будущем - чаще всего для проведения подспутниковых наблюдений (в целях верификации, атмосферной коррекции и пр.).
В статье описывается подход к моделированию проекций орбит ИСЗ на поверхность Земли с использованием доступных средств: библиотек языка Python и API сервиса space-track.org.
Входные параметры модели SGP4
Наиболее распространенной моделью для определения положения спутников на орбите является SGP (Simplified General Perturbations), различные модификации которой используются в оперативной работе по всему миру начиная с 70-х годов. Главная задача модели - вычислить скорость и геоцентрические координаты ИСЗ (X, Y, Z) на заданный момент времени, которые нетрудно пересчитать на поверхность эллипсоида, получив географические координаты проекции положения ИСЗ (широта, долгота). Сама модель достаточно сложна, хотя и сводится к линейным расчётам и удобна для алгоритмизации. Её описание и оригинальный FORTRAN-код можно найти в соответствующих документах [1,2].
В качестве входных параметров SGP использует данные телеметрии спутников в формате TLE (two-line element sets): это две линии по 69 символов, описывающие основные метаданные спутника и параметры телеметрии [3]. Содержание первой линии:
| Номер | Положение | Содержание | Пример |
|---|---|---|---|
| 1 | 01-01 | Номер строки | 1 |
| 2 | 03-07 | Номер спутника в базе данных NORAD | 25994 |
| 3 | 08-08 | Классификация (U=Unclassified — не секретный) | U |
| 4 | 10-11 | Международное обозначение (последние две цифры года запуска) | 99 |
| 5 | 12-14 | Международное обозначение (номер запуска в этом году) | 068 |
| 6 | 15-17 | Международное обозначение (часть запуска) | A |
| 7 | 19-20 | Год эпохи (последние две цифры) | 16 |
| 8 | 21-32 | Время эпохи (целая часть — номер дня в году, дробная — часть дня) | 052.07623983 |
| 9 | 34-43 | Первая производная от среднего движения (ускорение), деленная на два [виток/день^2] | .00001336 |
| 10 | 45-52 | Вторая производная от среднего движения, деленная на шесть (подразумевается, что число начинается с десятичного разделителя) [виток/день^3] | 00000-0 |
| 11 | 54-61 | Коэффициент торможения B* (подразумевается, что число начинается с десятичного разделителя) | 30635-3 |
| 12 | 63-63 | Изначально — типы эфемерид, сейчас — всегда число 0 | 0 |
| 13 | 65-68 | Номер (версия) элемента | 999 |
| 14 | 69-69 | Контрольная сумма по модулю 10 | 6 |
Собранный пример: 1 25994U 99068A 16052.07623983 .00001336 00000-0 30635-3 0 9996
Содержание второй линии:
| Номер | Положение | Содержание | Пример |
|---|---|---|---|
| 1 | 01-01 | Номер строки | 1 |
| 2 | 03-07 | Номер спутника в базе данных NORAD | 25994 |
| 3 | 09-16 | Наклонение в градусах | 98.1986 |
| 4 | 18-25 | Долгота восходящего узла в градусах | 128.0087 |
| 5 | 27-33 | Эксцентриситет (подразумевается, что число начинается с десятичного разделителя) | 0001485 |
| 6 | 35-42 | Аргумент перицентра в градусах | 109.3968 |
| 7 | 44-51 | Средняя аномалия в градусах | 250.7393 |
| 8 | 53-63 | Частота обращения (оборотов в день) (среднее движение) [виток/день] | 14.57136668 |
| 9 | 64-68 | Номер витка на момент эпохи | 86046 |
| 10 | 69-69 | Контрольная сумма по модулю 10 | 2 |
Собранный пример: 2 25994 98.1986 128.0087 0001485 109.3968 250.7393 14.57136668860462
Важно понимать, что такие эфемериды описывают мгновенное состояние ИСЗ, и, хотя описывают его поведение с довольно высокой точностью, при увеличении дальности прогноза (относительно данной эпохи) будут давать всё большую и большую ошибку.
Получение данных TLE
Данные TLE сегодня публикуются многими поставщиками (например, последние данные TLE по ряду спутников ДЗЗ на сайте ScanEx), но нам нужно получать не только свежие данные, но и архивные, для моделирования положений спутников в прошлом.
Одним из лучших в сети ресурсов представляется портал space-track.org, предоставляющий доступ к обширной информации о спутниках различного назначения. Очень важно, что space-track имеет REST API, позволяющее получать нужные данные максимально удобно. Требуется авторизация (и для доступа к интерфейсу, и для программного обращения к API), регистрация при этом бесплатная и открытая. Забегая вперёд, скажем в пользу space-track ещё то, что для работы с его API существует открытая python-библиотека.
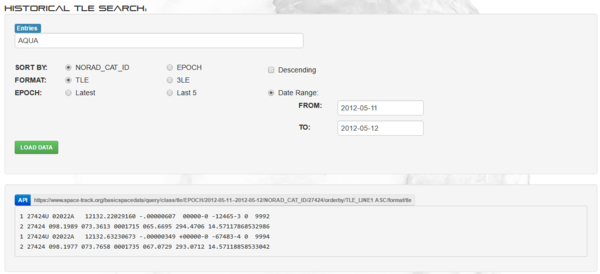
Непосредственно в интерфейсе сайта можно запрашивать данные TLE (в разделе Retrieve TLE Data by Satellite Catalog Number), заполнив небольшую форму с указанием названия или идентификатора спутника, а также интересующего вас периода времени. Для примера запросим данные TLE для спутника AQUA на середину мая 2012 года:
Результат вы получаете мгновенно. Примечательно, что сразу же при выдаче ответа сервис выводит команду API, соответствующую вашему запросу - это позволяет очень быстро разобраться в том, как оно организовано и как с ним работать.
https://www.space-track.org/basicspacedata/query/class/tle/EPOCH/2012-05-11--2012-05-12/NORAD_CAT_ID/27424/orderby/TLE_LINE1 ASC/format/tle
Выполнив этот запрос тут же в адресной строке браузера (т.е. реализовав простой HTTP-запрос), можно увидеть, что при работе с API данные представляются в незамысловатом текстовом виде, в котором их, учитывая строгую структуру формата, несложно интерпретировать программно.
В целом API подробно документировано. Для нашей задачи вполне достаточно рассмотреть тот пример, который был получен для майских приключений спутника AQUA. Изменяемыми в этой строке запроса будут всего два параметра:
- Диапазон дат (2012-05-11--2012-05-12), формат yyyy-mm-dd--yyyy-mm-dd;
- Идентификатор ИСЗ (27424).
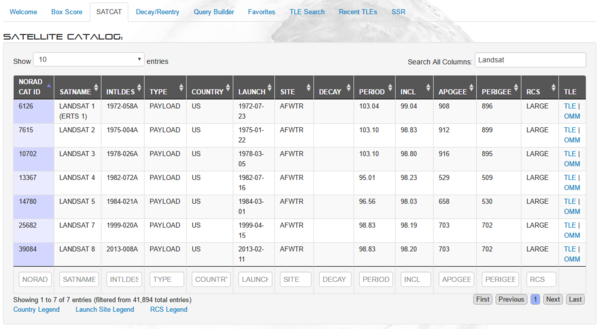
Идентификатор нужного вам ИСЗ можно найти там же, на space-track, в разделе SATCAT, в удобном интерактивном интерфейсе. Нас интересует первая колонка таблицы результатов поиска. Например, поищем идентификаторы спутников программы Landsat:
Landsat 8 соотвествует номеру 39084. Попробуем найти актуальные TLE для этого спутника, заодно посмотрев, как изменится структура запроса при использовании не диапазона дат, а опции "Latest", т.е. "последние данные". Запрос:
https://www.space-track.org/basicspacedata/query/class/tle_latest/ORDINAL/1/NORAD_CAT_ID/39084/orderby/TLE_LINE1%20ASC/format/tle
и ответ:
1 39084U 13008A 16354.79369944 .00000065 00000-0 24444-4 0 9999 2 39084 98.2045 61.9547 0001318 94.3108 265.8241 14.57119154204938
Как видно, порядок аргументов в запросе изменился.
Программная реализация
Открытая программная реализация модели SGP4 доступна для C++ и Python (библиотека pyorbital). Для примера будем использовать именно Python и pyorbital (есть и другая реализация на Python'e: python-sgp4). Для получения данных от API space-track.org доступна специальная библиотека. Чтобы представить результат в формате геоданных применим библиотеку pyshp. Поскольку за нас уже почти всё сделали, код очень прост. Разберём его по разделам.
Установка необходимых библиотек
Все библиотеки доступны в основном репозитории Python и устанавливаются очень просто
pip install pyorbital pip install spacetrack pip install pyshp
Получение данных space-track.org
# Импортируем библиотеки
# Штатная библиотека для работы со временем
from datetime import datetime, date
# Собственно клиент для space-track
# Набор операторов для управления запросами. Отсюда нам понадобится время
import spacetrack.operators as op
# Главный класс для работы с space-track
from spacetrack import SpaceTrackClient
# Имя пользователя и пароль сейчас опишем как константы
USERNAME = <YOUR SPACE-TRACK USERNAME>
PASSWORD = <YOUR SPACE-TRACK PASSWORD>
# Для примера реализуем всё в виде одной простой функции
# На вход она потребует идентификатор спутника, диапазон дат, имя пользователя и пароль. Опциональный флаг для последних данных tle
def get_spacetrack_tle (sat_id, start_date, end_date, username, password, latest=False):
# Реализуем экземпляр класса SpaceTrackClient, инициализируя его именем пользователя и паролем
st = SpaceTrackClient(identity=username, password=password)
# Выполнение запроса для диапазона дат:
if not latest:
# Определяем диапазон дат через оператор библиотеки
daterange = op.inclusive_range(start_date, end_date)
# Собственно выполняем запрос через st.tle
data = st.tle(norad_cat_id=sat_id, orderby='epoch desc', limit=1, format='tle', epoch = daterange)
# Выполнение запроса для актуального состояния
else:
# Выполняем запрос через st.tle_latest
data = st.tle_latest(norad_cat_id=sat_id, orderby='epoch desc', limit=1, format='tle')
# Если данные недоступны
if not data:
return 0, 0
# Иначе возвращаем две строки
tle_1 = data[0:69]
tle_2 = data[70:139]
return tle_1, tle_2
Представлена очень простая функция, использующая клиентскую библиотеку space-track для получения одного (первого из запроса) набора tle. Пример её использования:
# Запросим данные о положении Landsat 8 11 мая 2016 года
# Обратите внимание, что даты указываем в формате date(y,m,d)
tle_1, tle_2 = get_spacetrack_tle (39084, date(2016,5,11), date(2016,5,12), USERNAME, PASSWORD)
print tle_1, tle_2
>>> 1 39084U 13008A 16132.92196421 +.00000109 +00000-0 +34320-4 0 9999
>>> 2 39084 098.2260 203.0765 0001471 094.1169 266.0197 14.57124417160799
# А теперь данные об актуальном положении
tle_1, tle_2 = get_spacetrack_tle (39084, None, None, USERNAME, PASSWORD, True)
print tle_1, tle_2
>>> 1 39084U 13008A 16354.79369944 .00000065 00000-0 24444-4 0 9999
>>> 2 39084 98.2045 61.9547 0001318 94.3108 265.8241 14.57119154204938
Расчёт координат проекции спутника
# Импортируем библиотеки
# Штатная библиотека для работы со временем
from datetime import datetime, date
# Ключевой класс библиотеки pyorbital
from pyorbital.orbital import Orbital
# Ещё одна простая функция, для демонстрации принципа.
# На вход она потребует две строки tle и время utc в формате datetime.datetime
def get_lat_lon_sgp (tle_1, tle_2, utc_time):
# Инициализируем экземпляр класса Orbital двумя строками TLE
orb = Orbital("N", line1=tle_1, line2=tle_2)
# Вычисляем географические координаты функцией get_lonlatalt, её аргумент - время в UTC.
lon, lat, alt = orb.get_lonlatalt(utc_time)
return lon, lat
Пример использования:
# Используем данные TLE полученные вручную на space-track.org для спутника Terra
tle_1 = '1 25994U 99068A 16355.18348138 .00000089 00000-0 29698-4 0 9992'
tle_2 = '2 25994 98.2045 66.7824 0000703 69.9253 290.2059 14.57115924904601'
# Нас интересует текущий момент времени
utc_time = datetime.utcnow()
# Обращаемся к фукнции и выводим результат
lon, lat = get_lat_lon_sgp (tle_1, tle_2, utc_time)
print lon, lat
>>> 175.589796941 -13.6408377148
Создание набора геоданных с треком спутника
Теперь объединим получение данных space-track и расчёт положения спутника, добавив создание точечного шейп-файла. Зададимся целью написать функцию, которая бы создавала точечный шейп-файл с положениями спутника в течение указанных суток с заданным шагом по времени, в атрибуты каждой точки записывая широту, долготу и время пролёта.
# Импортируем библиотеки - для начала оговоренные ранее
from datetime import datetime, date, timedelta
import spacetrack.operators as op
from spacetrack import SpaceTrackClient
from pyorbital.orbital import Orbital
# И pyshp, которая понадобится для создания шейп-файла
import shapefile
# Имя пользователя и пароль
USERNAME = <YOUR SPACE-TRACK USERNAME>
PASSWORD = <YOUR SPACE-TRACK PASSWORD>
# Уже описанная ранее функция get_spacetrack_tle может использоваться без изменений
def get_spacetrack_tle (sat_id, start_date, end_date, username, password, latest=False):
st = SpaceTrackClient(identity=username, password=password)
if not latest:
daterange = op.inclusive_range(start_date, end_date)
data = st.tle(norad_cat_id=sat_id, orderby='epoch desc', limit=1, format='tle', epoch = daterange)
else:
data = st.tle_latest(norad_cat_id=sat_id, orderby='epoch desc', limit=1, format='tle')
if not data:
return 0, 0
tle_1 = data[0:69]
tle_2 = data[70:139]
return tle_1, tle_2
# А вот функция get_lat_lon_sgp нам уже не пригодится в своём виде
# ведь создавать экхемпляр класса Orbital для каждого момента времени
# не очень-то хочется
# На вход будем требовать идентификатор спутника, день (в формате date (y,m,d))
# шаг в минутах для определения положения спутника, путь для результирующего файла
def create_orbital_track_shapefile_for_day (sat_id, track_day, step_minutes, output_shapefile):
# Для начала получаем TLE
# Если запрошенная дата наступит в будущем, то запрашиваем самые последний набор TLE
if track_day > date.today():
tle_1, tle_2 = get_spacetrack_tle (sat_id, None, None, USERNAME, PASSWORD, True)
# Иначе на конкретный период, формируя запрос для указанной даты и дня после неё
else:
tle_1, tle_2 = get_spacetrack_tle (sat_id, track_day, track_day + timedelta(days = 1), USERNAME, PASSWORD, False)
# Если не получилось добыть
if not tle_1 or not tle_2:
print 'Impossible to retrieve TLE'
return
# Создаём экземляр класса Orbital
orb = Orbital("N", line1=tle_1, line2=tle_2)
# Создаём экземпляр класса Writer для создания шейп-файла, указываем тип геометрии
track_shape = shapefile.Writer(shapefile.POINT)
# Добавляем поля - идентификатор, время, широту и долготу
# N - целочисленный тип, C - строка, F - вещественное число
# Для времени придётся использовать строку, т.к. нет поддержки формата "дата и время"
track_shape.field('ID','N',40)
track_shape.field('TIME','C',40)
track_shape.field('LAT','F',40)
track_shape.field('LON','F',40)
# Объявляем счётчики, i для идентификаторов, minutes для времени
i = 0
minutes = 0
# Простой способ пройти сутки - с заданным в минутах шагом дойти до 1440 минут.
# Именно столько их в сутках!
while minutes < 1440:
# Расчитаем час, минуту, секунду (для текущего шага)
utc_hour = int(minutes // 60)
utc_minutes = int((minutes - (utc_hour*60)) // 1)
utc_seconds = int(round((minutes - (utc_hour*60) - utc_minutes)*60))
# Сформируем строку для атрибута
utc_string = str(utc_hour) + '-' + str(utc_minutes) + '-' + str(utc_seconds)
# И переменную с временем текущего шага в формате datetime
utc_time = datetime(track_day.year,track_day.month,track_day.day,utc_hour,utc_minutes,utc_seconds)
# Считаем положение спутника
lon, lat, alt = orb.get_lonlatalt(utc_time)
# Создаём в шейп-файле новый объект
# Определеяем геометрию
track_shape.point(lon,lat)
# и атрибуты
track_shape.record(i,utc_string,lat,lon)
# Не забываем про счётчики
i += 1
minutes += step_minutes
# Вне цикла нам осталось записать созданный шейп-файл на диск.
# Т.к. мы знаем, что координаты положений ИСЗ были получены в WGS84
# можно заодно создать файл .prj с нужным описанием
try:
# Создаем файл .prj с тем же именем, что и выходной .shp
prj = open("%s.prj" % output_shapefile.replace('.shp',''), "w")
# Создаем переменную с описанием EPSG:4326 (WGS84)
wgs84_wkt = 'GEOGCS["WGS 84",DATUM["WGS_1984",SPHEROID["WGS 84",6378137,298.257223563]],PRIMEM["Greenwich",0],UNIT["degree",0.0174532925199433]]'
# Записываем её в файл .prj
prj.write(wgs84_wkt)
# И закрываем его
prj.close()
# Функцией save также сохраняем и сам шейп.
track_shape.save(output_shapefile)
except:
# Вдруг нет прав на запись или вроде того...
print 'Unable to save shapefile'
return
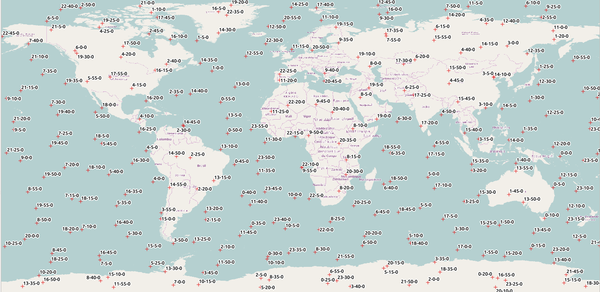
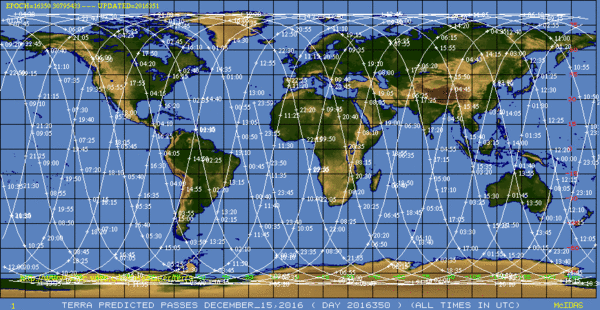
Вот и всё, давайте проверим, как это работает, и проверим корректность! Данные о положении спутника Terra с частотой 5 минут публикуются на специальном сервисе Space Science and Engineering Data Center, с ним и сверимся. Смоделируем положения на 15 декабря 2016 года и визуализируем получившийся набор геоданных в QGIS.
create_orbital_track_shapefile_for_day(25994, date(2016,12,15), 5, '/home/silent/space/terra_15_12_2016_5min.shp')
Настроив в QGIS подписи и подложив OSM получим следующую картинку:
Найдём данные на тот же день у Space Science and Engineering Data Center:
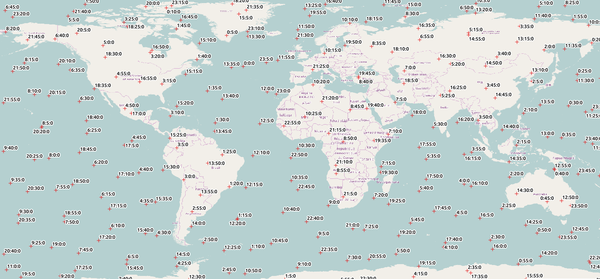
Всё прекрасно сходится! Узнаем, где будет Landsat 8 в будущем? Например, 22 декабря 2016.
create_orbital_track_shapefile_for_day(39084, date(2016,12,22), 5, '/home/silent/space/landsat_8_22_12_2016_5min.shp')
Представляя себе полосу съемки, можно оценить охват снятой территории за 1 день.
В коде показан механизм, который несложно приспособить под собственные задачи. Таким образом можно осуществлять автоматизацию поиска и загрузки архивных данных, прогнозирование пролётов. Важно помнить, что в зависимости от особенностей аппаратуры, установленной на спутнике, соотношение между треком пролёта и снятой территорий будет сильно разниться. К примеру, Sentinel-1 оснащен радиолокатором бокового обзора, его наблюдения не надирные; полосы съемки MODIS (Terra) и ETM+ (Landsat) отличаются на порядки по степени охвата (хотя треки похожи); и так далее.
Источники
2. David A. Vallado, Paul Crawford. SGP4 Orbit Determination