Создание треугольных сеток на сфере
Два-три предложения.
Постановка задачи
Регулярная...
Генерация сетки в сферическом треугольнике
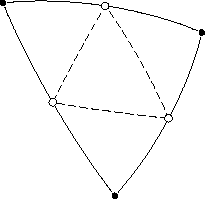
Процедуру создания на некоторой поверхности сетки треугольников обычно называют триангуляцией. В качестве базы для создания сетки используем некоторый сферический треугольник, заданный координатами своих вершин.
Метод бисекции
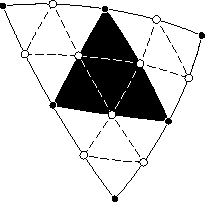
Назовём бисекцией операцию деления исходного треугольника на четыре треугольника нового поколения. Собственно термин «бисекция» относится к делению сторон пополам. В середины рёбер вставляются новые вершины (белые точки на рисунках), которые соединяются новыми рёбрами (пунктирные линии), образующими новые треугольники. Следующее поколение получается очередной бисекцией.
В терминах геометрии на сфере задача вставки точек в стороны треугольников решается последовательным решением обратной и прямой геодезических задач. Однако в данном случае гораздо проще использовать векторную алгебру. Пусть концы стороны заданы векторами a и b; тогда средняя точка f вычисляется как их нормированная сумма:
 Первая бисекция |
 Вторая бисекция |
 Трисекция |
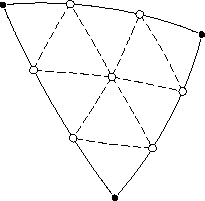
Метод трисекции
Исходный треугольник делится на девять треугольников нового поколения. В результате трисекции каждая сторона делится на три равных отрезка, в концы которых вставляются вершины. Итого шесть новых вершин, и седьмая вставляется в геометрический центр треугольника. Вершины соединяются рёбрами, образующими треугольники.
Проще всего вычислить положение центральной точки g:
где a, b и c — векторы вершин исходного треугольника.
Разделить стороны на три равных отрезка сложнее. Удобное решение предлагает утилита PROJ.4 geod:
$ geod +a=радиус_Земли +lat_1=широта_1 +lon_1=долгота_1 +lat_2=широта_2 +lon_2=долгота_2 +n_S=3
Здесь параметры lat_1, lon_1, lat_2, lon_2 задают начало и конец линии, а параметр n_S определяет число отрезков. Результатом будут широты и долготы четырёх точек, лежащих на равных расстояниях вдоль линии.
Сферические многогранники
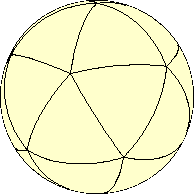
Сферический многогранник — разбиение сферы дугами больших окружностей на замкнутые области, называемые сферическими многоугольниками. Способы разбиения сферы ничем не ограничены. Однако регулярные построения обычно основаны на пространственной симметрии тетраэдра, октаэдра или икосаэдра.
Нас интересуют способы разбиения сферы на равносторонние или близкие к равносторонним треугольники. В центре такого треугольника построенная на его основе сетка будет близка к регулярной. Наибольшие искажения формы сетки будут вблизи углов базового треугольника. Несложный анализ показывает, что с позиции сохранения формы выгоднее всего опираться на симметрию икосаэдра. Подходящие многогранники — правильные и полуправильные, образованные треугольниками либо пяти- и шестиугольниками, которые разбиваются на почти равносторонние треугольники. Рассмотрим лишь несколько многогранников, удовлетворяющих этим требованиям.
 Икосаэдр |
 Пентакисдодекаэдр | |
 Икосододекаэдр |
 Усечённый икосаэдр |
 Курносый додекаэдр |
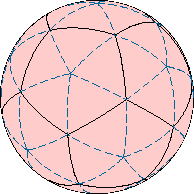
Икосаэдр — классическое Платоново тело, сложенное двадцатью равносторонними треугольниками.
Пентакисдодекаэдр. Сплошные линии — рёбра классического додекаэдра. Пунктирные линии, разделяя каждую грань додэкаэдра на треугольники, превращают его в пентакисдодэкаэдр.
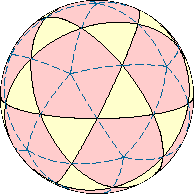
Икосододекаэдр образован жёлтыми треугольниками и красными пятиугольниками. Разделив пятиугольники на треугольники, как показано пунктирными линиями, получим основу для построения сетки. Полученная фигура не имеет самостоятельного значения, поскольку получается после бисекции граней икосаэдра.
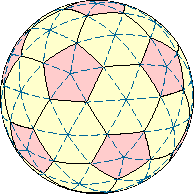
Усечённый икосаэдр, он же «футбольный мяч», образован жёлтыми шестиугольниками и красными пятиугольниками. Разделив их на треугольники, получим основу для построения сетки. Полученная фигура структурно совпадает с результатом трисекции граней икосаэдра, хотя геометрия немного отличается: из трёх частей, на которые разделено каждое ребро икосаэдра, средняя несколько длиннее крайних.
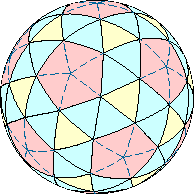
Курносый додэкаэдр образован жёлтыми и голубыми треугольниками и красными пятиугольниками. Разделив пятиугольники на треугольники, как показано пунктирными линиями, получим основу для построения сетки.
Во всех многогранниках с икосаэдрической симметрией получаются одни и те же искажения формы сетки, максимальные вблизи вершин образующего икосаэдра.