Полиномиальные преобразования - примеры реализации
по адресу http://gis-lab.info/qa/polynom-calc-examples.html
Математические выкладки решения задачи, применяемой при привязке данных
При операции географической привязки данных, то есть перевода данных из локальной системы координат в географическую или прямоугольную, сам пересчет обычно происходит "за сценой" и его особенности часто понятны пользователю только интуитивно. Эта статья использует математические выкладки алгоритма и показывает их реализацию, с помощью различных инструментов. Основная цель - быстрая интеграция кода в свое программное обеспечение и просто лучшее понимание процесса привязки.
Так как одно из наиболее часто используемых преобразований при привязке - полиномиальное преобразование 2-й степени, мы иллюстрируем наши рассчёты на его примере. Вычисления для аффинного преобразования (оно же полиномиальное преобразование 1-й степени) выполняются аналогичным образом, с меньшим количеством коэффициентов.
Математика
Математические выкладки описывающие аналитическое решение задачи приводятся в отдельной статье.
Тестовый набор данных
Для дальнейших пересчетов, зададим тестовый набор данных, на котором будем демонстрировать корректность вычислений. Данный пример иллюстрирует преобразование из локальной системы координат в прямоугольную (спроектированную), но на месте конечных координат могут быть и географического координаты долгота/широта.
|
Точка |
x |
y |
x' |
y' |
|
1 |
83.786 |
-36.107 |
557124.596 |
5479746.857 |
|
2 |
109.929 |
-582.929 |
564344.898 |
5376737.207 |
|
3 |
1038.000 |
-434.786 |
646174.994 |
5421503.083 |
|
4 |
539.107 |
-694.036 |
603772.500 |
5363472.000 |
|
5 |
831.036 |
-352.000 |
626857.500 |
5433468.000 |
|
6 |
632.786 |
-219.107 |
607905.000 |
5455042.500 |
Сделаем нашей тестовой точкой точку с координатами: x = 500 и y = -300. Используя возможности ERDAS IMAGINE получим его вариант предсказания: 596703.345492103, 5437370.8467262
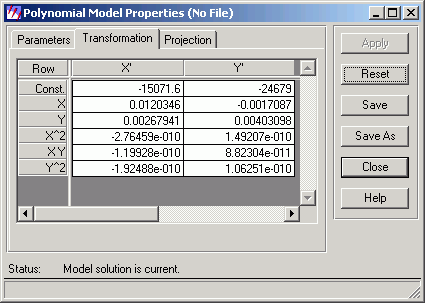
Так же, используя тот же инструмент ERDAS IMAGINE, посмотрим вычисленные им коэффициенты преобразования. Примечание: по какой-то причине, ERDAS IMAGINE показыват коэффициенты не прямой, а обратной задачи, поэтому при вычислении например в Excel, нужно будет поменять местами x,y и x',y'. Итак, для нашего тестового набора данных коэффициенты расчитанные ERDAS IMAGINE следующие:
Пример пересчета в Excel
Для быстрой проверки можно воспользоваться данной таблицей в MS Excel, которая использует вышеприведенные расчеты для вычисления трансформации и предсказания новых координат. С помощью этой таблицы, используем тестовый набор данных и сравним коэффициенты преобразования с полученными в ERDAS IMAGINE:
|
Коэффициент |
a |
b |
|
0 |
- 15071.583923079 | -24679.2116161184 |
|
1 (X) |
0.01203458721463060 | -0.0017086683749 |
|
2 (Y) |
0.00267941522144888 | 0.0040310417433 |
|
3 (X2) |
-0.00000000027645868 | 0.0000000001492 |
|
4 (XY) |
-0.00000000011992843 | 0.0000000000882 |
|
5 (Y2) |
-0.00000000019248837 | 0.0000000001062 |
Результат - не отличается от результата ERDAS IMAGINE.
Пример пересчета в R
Зададим исходные данные:
x = c(83.786,109.929,1038.000,539.107,831.036,632.786)
y = c(-36.107,-582.929,-434.786,-694.036,-352.000,-219.107)
x2 = c(557124.596,564344.898,646174.994,603772.500, 626857.5, 607905.000)
y2 = c(5479746.857,5376737.207,5421503.083,5363472.000,5433468.000,5455042.500)
Построим матрицу:
mat = matrix( c(1, 1, 1, 1, 1, 1, x, y, x^2, x*y, y^2), nrow = 6, ncol = 6)
И решим прямую задачу (x,y -> x2,y2) для нахождения коэффициентов a и b:
an = solve(mat, x2)
bn = solve(mat, y2)
Или обратную задачу (x,y <- x2,y2), для этого нам также понадобится переопределить матрицу:
matinv <- matrix( c(1, 1, 1, 1, 1, 1, x2, y2, x2^2, x2*y2, y2^2), nrow = 6, ncol = 6)
aninv = solve(matinv, x)
bninv = solve(matinv, y)
Результатом прямой задачи будут следующие наборы коэффициентов, для прямого преобразования:
<syntaxhighlight lang="rsplus">
[1] 5.493158e+05 8.948879e+01 -8.564444e+00 2.322324e-04 2.727497e-04 6.293799e-04
[1] 5.485053e+06 1.809379e+01 1.888970e+02 -2.225621e-04 -3.448929e-04 -6.190561e-04
Создадим тестовую точку и проверим результат:
testpoint = c(500, -300)
xpred = an[1] + an[2]* testpoint[1] + an[3]* testpoint[2] + an[4]* testpoint[1]^2 + an[5]* testpoint[1]*testpoint[2] + an[6]*testpoint[2]^2
ypred = bn[1] + bn[2]* testpoint[1] + bn[3]* testpoint[2] + bn[4]* testpoint[1]^2 + bn[5]* testpoint[1]*testpoint[2] + bn[6]*testpoint[2]^2
Наш результат:
596703.3
5437371.0
Что отличается от результатов ERDAS лишь на доли метра. Что и требовалось доказать.
Листы рассчётов для MathCad
Файлы представляют из себя лист рассчётов для среды MathCad (версия 11 и выше), где на примере показано как можно трансформировать координаты с использованием полиномиальных преобразований 1-го и 2-го порядков (скачать). Прислал Александр Г.
Процедура для пересчета на Delphi
Для расчетов также понадобится дополнительная библиотека для осуществления операций с матрицами.
map:record
pnts:array of record // набор точек для привязки карты
xr,yr,xg,yg:extended; // xr,yr - растровые координаты; xg,yg - географические координаты
end;
coeff_x:array of extended;
coeff_y:array of extended;
end;
function getx(x,y:extended):extended;var m:word;
begin
if length(main.map.coeff_x)>0 then getx:=main.map.coeff_x[1]+main.map.coeff_x[2]*x+main.map.coeff_x[3]*y+main.map.coeff_x[4]*x*x+main.map.coeff_x[5]*x*y+main.map.coeff_x[6]*y*y else getx:=-1;
end;
function gety(x,y:extended):extended;
begin
if length(main.map.coeff_y)>0 then gety:=main.map.coeff_y[1]+main.map.coeff_y[2]*x+main.map.coeff_y[3]*y+main.map.coeff_y[4]*x*x+main.map.coeff_y[5]*x*y+main.map.coeff_y[6]*y*y else gety:=-1;
end;
procedure map_calculate_ceeff;var aa:TReal2DArray;var i,j:byte;
begin
// вычисление коэффициентов полинома
//--------------------------------------------------------
// заполнение обратной матрицы
setlength(aa,7,7);
for i:=1 to 6 do begin
aa[1,i]:=1;
aa[2,i]:=main.map.pnts[i-1].xg;
aa[3,i]:=main.map.pnts[i-1].yg;
aa[4,i]:=main.map.pnts[i-1].xg*main.map.pnts[i-1].xg;
aa[5,i]:=main.map.pnts[i-1].xg*main.map.pnts[i-1].yg;
aa[6,i]:=main.map.pnts[i-1].yg*main.map.pnts[i-1].yg;
end;
// вычисление обратной матрицы
if Inverse(aa,6)=false then begin main.show_err('Ошибка. Необходим другой набор контрольных точек.');exit;end;
// умножение с обратной матрицей X
setlength(main.map.coeff_x,7);for j:=1 to 6 do main.map.coeff_x[j]:=0;
for i:=1 to 6 do for j:=1 to 6 do main.map.coeff_x[i]:=main.map.coeff_x[i]+aa[j,i]*main.map.pnts[j-1].xr;
// умножение с обратной матрицей Y
setlength(main.map.coeff_y,7);for j:=1 to 6 do main.map.coeff_y[j]:=0;
for i:=1 to 6 do for j:=1 to 6 do main.map.coeff_y[i]:=main.map.coeff_y[i]+aa[j,i]*main.map.pnts[j-1].yr;
end;
Процедура для пересчета на C#
Для расчетов также понадобится дополнительная библиотека для осуществления операций с матрицами. Библиотеку LU-декомпозиции для решения системы, а так же пример программы можно скачать здесь. Прислал Deshchenko Sergey.
using System;
namespace Transformation
{
class Program
{
static void Main()
{
double[] x1 = { 83.786, 109.929, 1038.000, 539.107, 831.036, 632.786 };
double[] y1 = { -36.107, -582.929, -434.786, -694.036, -352.000, -219.107 };
double[] x2 = { 557124.596, 564344.898, 646174.994, 603772.500, 626857.500, 607905.000 };
double[] y2 = { 5479746.857, 5376737.207, 5421503.083, 5363472.000, 5433468.000, 5455042.500 };
int n = 6;
int p = 6;
/*************************************************************************
Входные параметры:
m - Матрица системы.
Массив с нумерацией элементов [1..N, 1..N].
bForX - Правая часть для X.
bForY - Правая часть для Y.
Массив с нумерацией элементов [1..N, 1..N].
n - Размерность системы.
p - Количество точек.
a - Решение системы с X.
b - Решение системы с Y.
*************************************************************************/
double[,] m = new double[n + 1, n + 1];
double[] bForX = new double[n + 1];
double[] bForY = new double[n + 1];
double[] a = new double[n + 1];
double[] b = new double[n + 1];
for (int i = 0; i < p; i++)
{
m[1, 1] = n;
m[1, 2] = m[2, 1] += x1[i];
m[1, 3] = m[3, 1] += y1[i];
m[1, 4] = m[4, 1] = m[2, 2] += Math.Pow(x1[i], 2);
m[1, 5] = m[5, 1] = m[2, 3] = m[3, 2] += x1[i] * y1[i];
m[1, 6] = m[6, 1] = m[3, 3] += Math.Pow(y1[i], 2);
m[2, 4] = m[4, 2] += Math.Pow(x1[i], 3);
m[2, 5] = m[5, 2] = m[3, 4] = m[4, 3] += Math.Pow(x1[i], 2) * y1[i];
m[2, 6] = m[6, 2] = m[3, 5] = m[5, 3] += x1[i] * Math.Pow(y1[i], 2);
m[3, 6] = m[6, 3] += Math.Pow(y1[i], 3);
m[4, 4] += Math.Pow(x1[i], 4);
m[4, 5] = m[5, 4] += Math.Pow(x1[i], 3) * y1[i];
m[4, 6] = m[6, 4] = m[5, 5] += Math.Pow(x1[i], 2) * Math.Pow(y1[i], 2);
m[5, 6] = m[6, 5] += x1[i] * Math.Pow(y1[i], 3);
m[6, 6] += Math.Pow(y1[i], 4);
bForX[1] += x2[i];
bForX[2] += x1[i] * x2[i];
bForX[3] += y1[i] * x2[i];
bForX[4] += Math.Pow(x1[i], 2) * x2[i];
bForX[5] += x1[i] * y1[i] * x2[i];
bForX[6] += Math.Pow(y1[i], 2) * x2[i];
bForY[1] += y2[i];
bForY[2] += x1[i] * y2[i];
bForY[3] += y1[i] * y2[i];
bForY[4] += Math.Pow(x1[i], 2) * y2[i];
bForY[5] += x1[i] * y1[i] * y2[i];
bForY[6] += Math.Pow(y1[i], 2) * y2[i];
}
{
System.Console.Write("Error! Degenerate matrix A!");
System.Console.WriteLine();
System.Console.ReadKey();
return;
}
if (!linsolve.solvesystem(m, bForY, n, ref b))
{
System.Console.Write("Error! Degenerate matrix A!");
System.Console.WriteLine();
System.Console.ReadKey();
return;
}
double testPointX1 = 500;
double testPointY1 = -300;
double testPointX2 = a[1] + a[2] * testPointX1 + a[3] * testPointY1 + a[4] * Math.Pow(testPointX1, 2) + a[5] * testPointX1 * testPointY1 + a[6] * Math.Pow(testPointY1, 2);
double testPointY2 = b[1] + b[2] * testPointX1 + b[3] * testPointY1 + b[4] * Math.Pow(testPointX1, 2) + b[5] * testPointX1 * testPointY1 + b[6] * Math.Pow(testPointY1, 2);
System.Console.Write("X = " + testPointX2);
System.Console.WriteLine();
System.Console.Write("Y = " + testPointY2);
System.Console.WriteLine();
for (int i = 0; i < n; i++)
{
System.Console.WriteLine();
System.Console.Write("a[" + i + "] = " + a[i + 1]);
}
System.Console.WriteLine();
for (int i = 0; i < n; i++)
{
System.Console.WriteLine();
System.Console.Write("b[" + i + "] = " + b[i + 1]);
}
System.Console.ReadKey();
}
}
}