Создание треугольных сеток на сфере: различия между версиями
ErnieBoyd (обсуждение | вклад) |
ErnieBoyd (обсуждение | вклад) |
||
| Строка 394: | Строка 394: | ||
Поскольку максимальные искажения формы треугольников не зависят от сложности выбранного многогранника, выберем наиболее простой из рассмотренных, икосаэдр. | Поскольку максимальные искажения формы треугольников не зависят от сложности выбранного многогранника, выберем наиболее простой из рассмотренных, икосаэдр. | ||
Сориентируем оси координатной системы определённым образом, чтобы две вершины икосаэдра оказались в полюсах сферической системы координат. Получим | Сориентируем оси координатной системы определённым образом, чтобы две вершины икосаэдра оказались в полюсах сферической системы координат. Получим следующие координаты вершин: | ||
{| class="wikitable" | {| class="wikitable" | ||
Версия от 11:32, 17 апреля 2014
Два-три предложения.
Постановка задачи
Требуется создать регулярное покрытие сферы треугольниками, близкими по размеру и форме. В качестве эталона примем сетку, образованную на плоскости равносторонними треугольниками. Отличие геометрии треугольника от правильной равносторонней будем интерпретировать как искажение формы.
В начале рассмотрим алгоритм построения сетки в базовом сферическом треугольнике. Затем уделим внимание различным способам разделения сферы на базовые сферические треугольники. Наконец, представим пример создания треугольной сетки на основе икосаэдра.
Генерация сетки в сферическом треугольнике
Процедуру создания на некоторой поверхности сетки треугольников обычно называют триангуляцией. В качестве базы для создания сетки используем некоторый сферический треугольник, заданный координатами своих вершин.
Метод бисекции
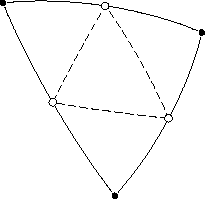
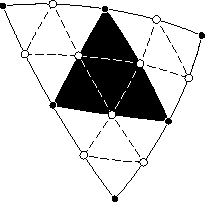
Назовём бисекцией операцию деления исходного треугольника на четыре треугольника нового поколения. Собственно термин «бисекция» относится к делению сторон пополам. В середины рёбер вставляются новые вершины (белые точки на рисунках), которые соединяются новыми рёбрами (пунктирные линии), образующими новые треугольники. Следующее поколение получается очередной бисекцией.
В терминах геометрии на сфере задача вставки точек в стороны треугольников решается последовательным решением обратной и прямой геодезических задач. Однако в данном случае гораздо проще использовать векторную алгебру. Пусть концы стороны заданы векторами a и b; тогда средняя точка f вычисляется как их нормированная сумма:
Метод трисекции
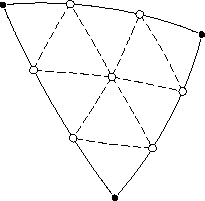
Исходный треугольник делится на девять треугольников нового поколения. В результате трисекции каждая сторона делится на три равных отрезка, в концы которых вставляются вершины. Итого шесть новых вершин, и седьмая вставляется в геометрический центр треугольника. Вершины соединяются рёбрами, образующими треугольники.
Проще всего вычислить положение центральной точки g:
где a, b и c — векторы вершин исходного треугольника.
Разделить стороны на три равных отрезка сложнее. Удобное решение предлагает утилита PROJ.4 geod:
$ geod +a=радиус_Земли +lat_1=широта_1 +lon_1=долгота_1 +lat_2=широта_2 +lon_2=долгота_2 +n_S=3
Здесь параметры lat_1, lon_1, lat_2, lon_2 задают начало и конец линии, а параметр n_S определяет число отрезков. Результатом будут широты и долготы четырёх точек, лежащих на равных расстояниях вдоль линии.
Программная реализация
Приведём пример программы на Си генерации сетки в треугольнике, реализующей метод бисекции:
/* ========================================================================== *
* triangulate
*
* Программа генерирует треугольную сетку в сферическом треугольнике.
*
* Usage: triangulate <triangle> <sections>
*
* Arguments:
* triangle - файл с координатами трёх точек
* sections - количество бисекций
* ========================================================================== */
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include "triangulate.h"
int main(int argc, char *argv[])
{
s_tri *tri;
char buf[1024], basename[1024], fname[1024], *ptr;
int i, j, k, n, zoom, n_tri;
int m, m0, m1;
double x[3], y[2], lon, lat;
FILE *fp;
if (argc < 3) {
puts("Usage: triangulate <triangle> <bisections>");
exit(EXIT_SUCCESS);
}
zoom = atoi(argv[2]);
strcpy(basename, argv[1]);
if ((ptr = strrchr(basename, '.')) != NULL)
*ptr = '\0';
/* рассчитать число треугольников всех уровней */
n = 1; /* число отрезков разбиения базового треугольника */
n_tri = 1; /* полная сумма треугольников */
for (k = 0; k < zoom; k++) {
n <<= 1; /* бисекция */
n_tri += n * n; /* добавить треугольники к сумме */
}
/* выделить память под треугольники */
if ((tri = calloc(n_tri, sizeof(s_tri))) == NULL) {
printf("can't allocate %d triangles\n", n_tri);
exit(EXIT_FAILURE);
}
/* прочесть координаты точек базового треугольника */
if ((fp = fopen(argv[1], "r")) == NULL) {
printf("can't open %s\n", argv[1]);
exit(EXIT_FAILURE);
}
for (i = 0; i < 3; i++) {
if (fgets(buf, 1024, fp) == NULL) {
printf("error reading %s\n", argv[1]);
exit(EXIT_FAILURE);
}
sscanf(buf, "%lf %lf", &lon, &lat);
y[0] = Radians(lon);
y[1] = Radians(lat);
SpherToCart(y, tri[0].pt[i]);
}
fclose(fp);
/* начать вывод в файл точек */
strcpy(fname, basename);
strcat(fname, "_p.MIF");
if ((fp = fopen(fname, "w")) == NULL) {
printf("can't create %s\n", fname);
exit(EXIT_FAILURE);
}
fputs("Version 300\n", fp);
fputs("Charset \"WindowsCyrillic\"\n", fp);
fputs("Delimiter \",\"\n", fp);
fputs("CoordSys Earth Projection 1, 0\n", fp);
fputs("Columns 1\n", fp);
fputs(" id Decimal(10, 0)\n", fp);
fputs("Data\n", fp);
fputs("\n", fp);
for (i = 0; i < 3; i++) {
CartToSpher(tri[0].pt[i], y);
fprintf(fp, "Point %f %f\n", Degrees(y[0]), Degrees(y[1]));
fputs(" Symbol (49,0,12) \n", fp);
}
tri[0].full = 1;
n = 1; /* число отрезков разбиения базового треугольника */
m0 = 0; /* номер 1-го треугольника предыдущего уровня */
m1 = 1; /* номер 1-го треугольника следующего уровня */
for (k = 0; k < zoom; k++) {
n <<= 1; /* бисекция */
for (m = 0; m < m1 - m0; m++) {
InsertPoint(tri[m0 + m].pt[1], tri[m0 + m].pt[2], tri[m1 + m*4].pt[0]);
InsertPoint(tri[m0 + m].pt[2], tri[m0 + m].pt[0], tri[m1 + m*4].pt[1]);
InsertPoint(tri[m0 + m].pt[0], tri[m0 + m].pt[1], tri[m1 + m*4].pt[2]);
tri[m1 + m*4].full = !tri[m0 + m].full;
memcpy(tri[m1 + m*4 + 1].pt[0], tri[m0 + m].pt[0], sizeof(double) * 3);
memcpy(tri[m1 + m*4 + 1].pt[1], tri[m1 + m*4].pt[2], sizeof(double) * 3);
memcpy(tri[m1 + m*4 + 1].pt[2], tri[m1 + m*4].pt[1], sizeof(double) * 3);
tri[m1 + m*4 + 1].full = tri[m0 + m].full;
memcpy(tri[m1 + m*4 + 2].pt[0], tri[m1 + m*4].pt[2], sizeof(double) * 3);
memcpy(tri[m1 + m*4 + 2].pt[1], tri[m0 + m].pt[1], sizeof(double) * 3);
memcpy(tri[m1 + m*4 + 2].pt[2], tri[m1 + m*4].pt[0], sizeof(double) * 3);
tri[m1 + m*4 + 2].full = tri[m0 + m].full;
memcpy(tri[m1 + m*4 + 3].pt[0], tri[m1 + m*4].pt[1], sizeof(double) * 3);
memcpy(tri[m1 + m*4 + 3].pt[1], tri[m1 + m*4].pt[0], sizeof(double) * 3);
memcpy(tri[m1 + m*4 + 3].pt[2], tri[m0 + m].pt[2], sizeof(double) * 3);
tri[m1 + m*4 + 3].full = tri[m0 + m].full;
if (!tri[m0 + m].full)
continue;
/* вывести точки */
for (j = 0; j < 3; j++) {
CartToSpher(tri[m1+m*4].pt[j], y);
fprintf(fp, "Point %f %f\n", Degrees(y[0]), Degrees(y[1]));
fputs(" Symbol (49,0,12) \n", fp);
}
i += 3;
}
m0 = m1;
m1 += n * n;
}
fclose(fp);
/* создать атрибуты точек */
strcpy(fname, basename);
strcat(fname, "_p.MID");
if ((fp = fopen(fname, "w")) == NULL) {
printf("can't create %s\n", fname);
exit(EXIT_FAILURE);
}
for (i = 0; i < (n + 1) * (n + 2) / 2; i++)
fprintf(fp, "%d\n", i + 1);
fclose(fp);
/*
* Вывод треугольников
*/
/* вывести треугольники в файл полигонов */
strcpy(fname, basename);
strcat(fname, "_a.MIF");
if ((fp = fopen(fname, "w")) == NULL) {
printf("can't create %s\n", fname);
exit(EXIT_FAILURE);
}
fputs("Version 300\n", fp);
fputs("Charset \"WindowsCyrillic\"\n", fp);
fputs("Delimiter \",\"\n", fp);
fputs("CoordSys Earth Projection 1, 0\n", fp);
fputs("Columns 1\n", fp);
fputs(" id Decimal(10, 0)\n", fp);
fputs("Data\n", fp);
fputs("\n", fp);
n = 1;
m0 = 0;
m1 = 1;
for (k = 0; k < zoom; k++) {
n <<= 1;
m0 = m1;
m1 += n * n;
}
for (m = 0; m < m1 - m0; m++) {
fputs("Region 1\n", fp);
fputs(" 4\n", fp);
for (j = 0; j <= 3; j++) {
i = j % 3;
CartToSpher(tri[m0+m].pt[i], y);
fprintf(fp, "%f %f\n", Degrees(y[0]), Degrees(y[1]));
}
fputs(" Pen (1,2,0) \n", fp);
fputs(" Brush (1,0,16777215)\n", fp);
for (j = 0; j < 3; j++)
x[j] = tri[m0 + m].pt[0][j]
+ tri[m0 + m].pt[1][j] + tri[m0 + m].pt[2][j];
CartToSpher(x, y);
fprintf(fp, " Center %f %f\n", Degrees(y[0]), Degrees(y[1]));
}
fclose(fp);
/* создать атрибуты полигонов */
strcpy(fname, basename);
strcat(fname, "_a.MID");
if ((fp = fopen(fname, "w")) == NULL) {
printf("can't create %s\n", fname);
exit(EXIT_FAILURE);
}
n = 1;
m0 = 0;
m1 = 1;
for (k = 0; k < zoom; k++) {
n <<= 1;
m0 = m1;
m1 += n * n;
}
for (m = 0; m < m1 - m0; m++)
fprintf(fp, "%d\n", m + 1);
fclose(fp);
/*
* Вывод линий
*/
/* вывести рёбра в файл линий */
strcpy(fname, basename);
strcat(fname, "_l.MIF");
if ((fp = fopen(fname, "w")) == NULL) {
printf("can't create %s\n", fname);
exit(EXIT_FAILURE);
}
fputs("Version 300\n", fp);
fputs("Charset \"WindowsCyrillic\"\n", fp);
fputs("Delimiter \",\"\n", fp);
fputs("CoordSys Earth Projection 1, 0\n", fp);
fputs("Columns 1\n", fp);
fputs(" id Decimal(10, 0)\n", fp);
fputs("Data\n", fp);
fputs("\n", fp);
n = 1;
m0 = 0;
m1 = 1;
for (k = 0; k < zoom; k++) {
n <<= 1;
m0 = m1;
m1 += n * n;
}
for (m = 0; m < m1 - m0; m++) {
if (!tri[m0 + m].full)
continue;
CartToSpher(tri[m0+m].pt[0], y);
for (j = 0; j < 3; j++) {
fputs("Pline 2\n", fp);
fprintf(fp, "%f %f\n", Degrees(y[0]), Degrees(y[1]));
i = (j + 1) % 3;
CartToSpher(tri[m0+m].pt[i], y);
fprintf(fp, "%f %f\n", Degrees(y[0]), Degrees(y[1]));
fputs(" Pen (1,2,0) \n", fp);
}
}
/* создать атрибуты линий */
strcpy(fname, basename);
strcat(fname, "_l.MID");
if ((fp = fopen(fname, "w")) == NULL) {
printf("can't create %s\n", fname);
exit(EXIT_FAILURE);
}
j = 0;
n = 1;
m0 = 0;
m1 = 1;
for (k = 0; k < zoom; k++) {
n <<= 1;
m0 = m1;
m1 += n * n;
}
for (m = 0; m < m1 - m0; m++)
if (tri[m0 + m].full)
for (i = 0; i < 3; i++)
fprintf(fp, "%d\n", ++j);
fclose(fp);
free(tri);
return 0;
}
Полный текст кода со вспомогательными функциями находится в файле triangulate.c в архиве Sph_tri.zip. Файл triangulate.h содержит необходимые объявления:
#define Radians(x) (x / 57.29577951308232)
#define Degrees(x) (x * 57.29577951308232)
/* структура треугольника */
typedef struct {
double pt[3][3]; /* координаты вершин */
int full; /* 0 - "пустой", 1 - "полный" */
} s_tri;
void InsertPoint(double a[],double b[],double c[]);
double CartToSpher(double x[],double y[]);
void SpherToCart(double y[],double x[]);
int main(int argc,char *argv[]);
Создадим исполняемый модуль triangulate компилятором gcc:
$ gcc -o triangulate triangulate.c -lm
Готовый исполняемый модуль для MS Windows triangulate.exe можно найти в архиве Sph_tri-win32.zip.
Программа запускается в командной строке с двумя аргументами. Первый аргумент — название файла, содержащего координаты вершин базового треугольники. Это должен быть текстовый файл, и в первых трёх строках он должен содержать значения координат «долгота широта» в десятичных градусах, разделённые пробелом или табуляцией. Второй аргумент — количество бисекций.
На выходе создаются файлы сетки отдельно для вершин, рёбер и фасеток.
Долготы всех точек в выходных файлах находятся в диапазоне от −180° до +180°.
В качестве координатной системы указана «долгота/широта неопределённая»: "CoordSys Earth Projection 1, 0". Для использования результатов в программах ГИС необходимо заменить ноль на требуемый код датума. Так, для WGS 84 следует подставить 104, для сферы Google — 157, а для Pulkovo-42 (Hungary) — 1001. Можно использовать и полную нотацию с явным указанием параметров преобразования Молоденского или Бурша-Вольфа; детали изложены в руководствах пользователя MapInfo Professional.
Сферические многогранники
Сферический многогранник — разбиение сферы дугами больших окружностей на замкнутые области, называемые сферическими многоугольниками. Способы разбиения сферы ничем не ограничены. Однако регулярные построения обычно основаны на пространственной симметрии тетраэдра, октаэдра или икосаэдра.
Нас интересуют способы разбиения сферы на равносторонние или близкие к равносторонним треугольники. В центре такого треугольника построенная на его основе сетка будет близка к регулярной. Наибольшие искажения формы сетки будут вблизи углов базового треугольника. Несложный анализ показывает, что с позиции сохранения формы выгоднее всего опираться на симметрию икосаэдра. Подходящие многогранники — правильные и полуправильные, образованные треугольниками либо пяти- и шестиугольниками, которые разбиваются на почти равносторонние треугольники. Рассмотрим лишь несколько многогранников, удовлетворяющих этим требованиям.
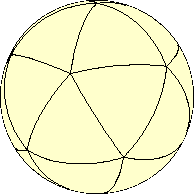
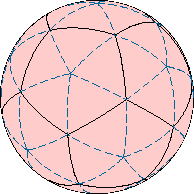
Икосаэдр — классическое Платоново тело, сложенное двадцатью равносторонними треугольниками.
Пентакисдодекаэдр. Сплошные линии — рёбра классического додекаэдра. Пунктирные линии, разделяя каждую грань додэкаэдра на треугольники, превращают его в пентакисдодэкаэдр.
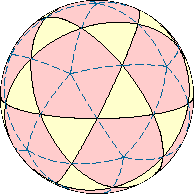
Икосододекаэдр образован жёлтыми треугольниками и красными пятиугольниками. Разделив пятиугольники на треугольники, как показано пунктирными линиями, получим основу для построения сетки. Полученная фигура не имеет самостоятельного значения, поскольку получается после бисекции граней икосаэдра.
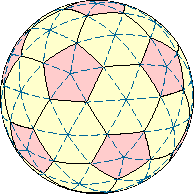
Усечённый икосаэдр, он же «футбольный мяч», образован жёлтыми шестиугольниками и красными пятиугольниками. Разбив все грани на треугольники, получим основу для построения сетки. Полученная фигура структурно совпадает с результатом трисекции граней икосаэдра, хотя геометрия немного отличается: из трёх частей, на которые разделено каждое ребро икосаэдра, средняя несколько длиннее крайних.
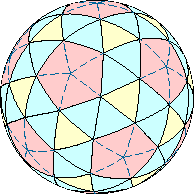
Курносый додэкаэдр образован жёлтыми и голубыми треугольниками и красными пятиугольниками. Разбив пятиугольники на треугольники, получим основу для построения сетки.
Во всех многогранниках с икосаэдрической симметрией получаются одни и те же искажения формы сетки, максимальные вблизи вершин образующего икосаэдра. Внутренний угол треугольников, сходящихся в вершине икосаэдра, равен 72° при эталонном 60°.
Пример создания треугольной сетки на основе икосаэдра
Поскольку максимальные искажения формы треугольников не зависят от сложности выбранного многогранника, выберем наиболее простой из рассмотренных, икосаэдр.
Сориентируем оси координатной системы определённым образом, чтобы две вершины икосаэдра оказались в полюсах сферической системы координат. Получим следующие координаты вершин:
| № | λ | φ |
|---|---|---|
| 1. | 0 | 90 |
| 2. | -180 | 26.5650511771 |
| 3. | -108 | 26.5650511771 |
| 4. | -36 | 26.5650511771 |
| 5. | 36 | 26.5650511771 |
| 6. | 108 | 26.5650511771 |
| 7. | -144 | -26.5650511771 |
| 8. | -72 | -26.5650511771 |
| 9. | 0 | -26.5650511771 |
| 10. | 72 | -26.5650511771 |
| 11. | 144 | -26.5650511771 |
| 12. | 0 | -90 |