Вычисление площади полигона на сфере и на эллипсоиде

Эта страница является черновиком статьи.

Одна-две фразы по существу.

Общие положения

Многоугольник на сфере

Определим полигон как простой многоугольник — участок поверхности, ограниченный замкнутой полилинией без самопересечений.

Полилиния в свою очередь — ломаная, образованная отрезками геодезических линий.

Геодезическая линия на плоскости — это прямая; геодезическая линия на сфере — дуга большой окружности.

Полный поворот контура

В общем случае определение площади многоугольника на искривлённой поверхности — нетривиальная задача. Нужно интегрировать по поверхности с пределами, заданными неявно. К счастью, математика может предложить обходные пути решения задачи.

Представим себе точку, движущуюся вдоль контура полигона. Вершины являются точками поворота. Внутренний угол при вершине θ равен разности направлений α в предыдущую и следующую вершины, а поворот есть угол τ, смежный внутреннему:

${\begin{array}{rcl}\theta _{i}&=&\alpha _{i,i-1}-\alpha _{i,i+1}\\\tau _{i}&=&\pi -\theta _{i}\end{array}}$

На евклидовой плоскости, обойдя любой замкнутый контур без самопересечений, точка совершает поворот ровно на одну окружность — 360°, или 2π радиан. В случае многоугольника этот поворот складывается из суммы поворотов в вершинах.

На поверхности с ненулевой гауссовой кривизной общий поворот отличается от 2π на величину избытка или недостатка, пропорционального кривизне поверхности и площади фигуры.

Площадь полигона на сфере

Сферический избыток

В общем случае кривизна поверхности меняется в каждой точке, но не на сфере! Кривизна сферы постоянна, и площадь замкнутой фигуры однозначно соотносится с полным поворотом контура.

Отличие полного поворота от 2π радиан называется сферическим избытком ε, который пропорционален площади полигона S:

${\begin{array}{rcl}\varepsilon &=&2\pi -\displaystyle \sum _{i=1}^{n}\tau _{i}\\S&=&\varepsilon R^{2}\end{array}}$

где R — радиус сферы.

Алгоритм вычисления площади

Пусть n-угольник задан координатами вершин φ_i, λ_i, где φ_i — широта i-ой вершины, λ_i — долгота, i = 1, … , n.

1. Для каждой стороны из решения обратной геодезической задачи для её конечных вершин находим прямые и обратные азимуты α_{i, i+1} и α_{i+1, i}.
2. Для каждой вершины по азимутам α_{i, i−1} в предыдущую и α_{i, i+1} в последующую вершины находим поворот τ_i и добавляем его к полному повороту τ.
3. Вычисляем сферический избыток ε.
4. Вычисляем площадь полигона S.

Радиус сферы

Радиус сферы выбирается таким образом, чтобы минимизировать погрешности, вызванные тем, что кривизна земной поверхности в разных точках различна.

В геодезической и картографической практике в качестве модели Земли принимают эллипсоид вращения, характеризуемый величинами экваториального радиуса a и сжатия f. Соответствующая сфера должна иметь такую же площадь, как и принимаемый за основу эллипсоид. Такая сфера называется эквивалентной (authalic sphaera по латыни).

Ниже мы приведём формулы вычисления радиуса эквивалентной сферы по параметрам эллипсоида. Пока же поближе посмотрим на пару-тройку популярных программных пакетов.

MapInfo — единственная известная нам программа, вычисляющая площади на сфере по умолчанию. Несложные эксперименты («реверс-инжиниринг») показывает, что радиус сферы не зависит от того, на каком эллипсоиде построена координатная система обрабатываемых данных, — он всегда равен 6370997 метров ровно. Анализ используемых земных эллипсоидов показывает, что это соответствует радиусу эквивалентной сферы эллипсоида Кларка 1866 года, определяемого величинами экаториального радиуса a = 6378206.4 м и полярного радиуса b = 6356583.8 м; точное значение радиуса R_auth = 6370997.2406 м, округлённое до метра — 6370997 м.

Выбор именно этого радиуса не случаен: эллипсоид Кларка 1866 по сей день широко используется в странах Северной Америки в картографических и кадастровых целях.

В большинстве своём программы GIS не вычисляют площадей на сфере. Тем не менее, в картографических целях ArcGIS включает два эллипсоида с характерными названиями: “Authalic sphere (ARCINFO)” (код “SPHEROID["Sphere_ARC_INFO",6370997,0]”) и более новый “Authalic sphere” (код “SPHEROID["Sphere",6371000,0]”).

В пакете PROJ.4 также имеется эллипсоид “sphere”: параметры “a=6370997.0”, “b=6370997.0”, описание “Normal Sphere (r=6370997)”.

Площади малых полигонов

Если полигон настолько мал, что сферический избыток сравним с погрешностью его вычисления, можно перейти к вычислениям площади на плоскости.

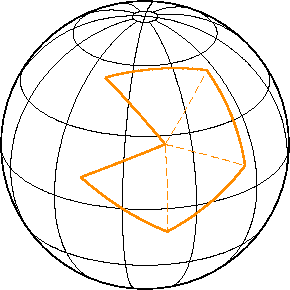
Для промежуточной по размерам зоны имеется следующий вариант решения проблемы. Полигон разбивается на сферические треугольники (на рисунке это показано пунктирными линиями). Решаются обратные задачи для каждой линии, из чего находятся длины сторон и внутренние углы каждого треугольника. После этого ε треугольников вычисляются, например, по первой формуле Каньоли:

$\sin {\frac {\varepsilon }{2}}={\frac {\sin {\frac {a}{2}}\sin {\frac {b}{2}}}{\cos {\frac {c}{2}}}}\sin C$

В учебниках сферической тригонометрии можно найти и другие формулы вычисления эксцесса.

Ссылки

• Задачи на сфере: обратная геодезическая задача
• Earth radius
• Краткий справочник по сферической тригонометрии
• Earth radius
• Latitude Developments Connected with Geodesy and Cartography with Tables including a Table for Lambert equal-area Meridional Projection
• Степанов Н. Н. Сферическая тригонометрия