Библиотека сетевого анализа QGIS: описание и примеры: различия между версиями
Stopa85 (обсуждение | вклад) Нет описания правки |
Stopa85 (обсуждение | вклад) Нет описания правки |
||
| Строка 118: | Строка 118: | ||
Алгоритм Дейкстры находит оптимальный маршрут от одной из вершин графа до всех остальных и значение оптимизируемого параметра. Хорошим способов представления результата выполнения алгоритма Дейкстры является [http://en.wikipedia.org/wiki/Shortest_path_tree дерево кратчайших путей]. | Алгоритм Дейкстры находит оптимальный маршрут от одной из вершин графа до всех остальных и значение оптимизируемого параметра. Хорошим способов представления результата выполнения алгоритма Дейкстры является [http://en.wikipedia.org/wiki/Shortest_path_tree дерево кратчайших путей]. | ||
[[Файл:network-analysis-02.png| | {| | ||
|- | |||
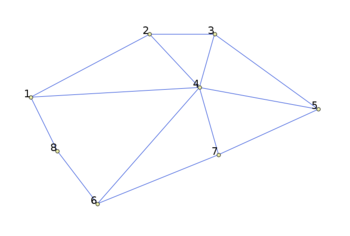
| [[Файл:network-analysis-01.png|350px|thumb|left|<center>Исходный граф</center>]] || | |||
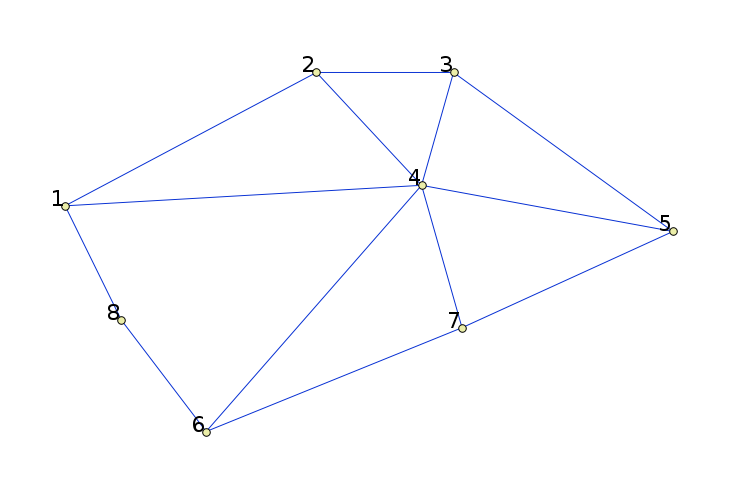
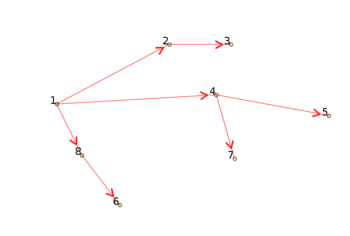
[[Файл:network-analysis-02.png|350px|thumb|right|<center>Дерево кратчайших путей с корнем в вершине №1.</center>]] | |||
|} | |||
Дерево кратчайших путей - это ориентированный взвешенный граф (точнее дерево) обладающий следующими свойствами: | Дерево кратчайших путей - это ориентированный взвешенный граф (точнее дерево) обладающий следующими свойствами: | ||
| Строка 125: | Строка 129: | ||
* Если вершина B достижима из вершины A, то путь соединяющий их единственный и он же кратчайший (оптимальный) на исходном графе. | * Если вершина B достижима из вершины A, то путь соединяющий их единственный и он же кратчайший (оптимальный) на исходном графе. | ||
Дерево кратчайших путей можно получить пользуясь методом shortestTree или методом dijkstra класса [http://doc.qgis.org/api/classQgsGraphAnalyzer.html QgsGraphAnalyzer]. | Дерево кратчайших путей можно получить пользуясь методом shortestTree или методом dijkstra класса [http://doc.qgis.org/api/classQgsGraphAnalyzer.html QgsGraphAnalyzer]. Рекомендуется пользоваться именно методом <tt>dijkstra</tt>. Он работает быстрее и в общем случае эффективнее расходует память. Метод <tt>shortestTree</tt> - может быть полезен, в тех случаях если хотите совершить обход дерева кратчайших путей. | ||
Метод <tt>shortestTree</tt> создает новый графовый объект (всегда QgsGraph) и принимает три аргумента: | Метод <tt>shortestTree</tt> создает новый графовый объект (всегда QgsGraph) и принимает три аргумента: | ||
| Строка 142: | Строка 146: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Вот так выглядит простейший способ отобразить дерево кратчайших путей для метода shortestTree (только замените координаты начальной точки на свои, а также выделите слой дорог в списке слоёв карты) | Вот так выглядит простейший способ отобразить дерево кратчайших путей для метода <tt>shortestTree</tt> (только замените координаты начальной точки на свои, а также выделите слой дорог в списке слоёв карты) | ||
<syntaxhighlight lang="python"> | <syntaxhighlight lang="python"> | ||
from PyQt4.QtCore import * | from PyQt4.QtCore import * | ||
| Строка 180: | Строка 184: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Так для метода dijkstra: | Так для метода <tt>dijkstra</tt>: | ||
<syntaxhighlight lang="python"> | <syntaxhighlight lang="python"> | ||
| Строка 222: | Строка 226: | ||
==== Нахождение кратчайших путей ==== | ==== Нахождение кратчайших путей ==== | ||
Для получения кратчайшего маршрута между двумя произвольными точками используется следующий подход. Обе точки (начальная A и конечная B) «привязываются» к графу на этапе построения, затем при помощи метода shortestTree получаем дерево кратчайших маршрутов с корнем в начальной точке A. В этом же дереве находим конечную точку B. Начинаем спуск по дереву от точки B к точке А. | Для получения кратчайшего маршрута между двумя произвольными точками используется следующий подход. Обе точки (начальная A и конечная B) «привязываются» к графу на этапе построения, затем при помощи метода <tt>shortestTree</tt> или <tt>dijkstra</tt> получаем дерево кратчайших маршрутов с корнем в начальной точке A. В этом же дереве находим конечную точку B. Начинаем спуск по дереву от точки B к точке А. Алгоритм можно записать так: | ||
# | # Присвоим Т = B | ||
# | # Пока Т <> A Цикл | ||
# | ## Добавим в маршрут точку Т | ||
# | ## Берем ребро, которое входит в точку Т | ||
## Находим точку ТТ, из которой это ребро выходит | |||
## Присваиваем Т = ТТ | |||
# Добавим в маршрут точку А | |||
На этом построение маршрута закончено. Вы получили список вершин, в обратном порядке, которые будут посещены при движении по кратчайшему маршруту. | |||
Посмотрите еще раз на [[Медиа:network-analysis-02.png| | Посмотрите еще раз на [[Медиа:network-analysis-02.png|дерево кратчайших путей]] и представьте что вы можете двигаться только против направления стрелочек. Двигайтесь из точки №7. Рано или поздно вы попадете в точку №1 (корень дерева) и не сможете двигаться дальше . | ||
Вот работающий пример для Консоли Python QGIS (только замените координаты начальной и конечной точки на свои, а также выделите слой дорог в списке слоёв карты) | Вот работающий пример для Консоли Python QGIS (только замените координаты начальной и конечной точки на свои, а также выделите слой дорог в списке слоёв карты) | ||
| Строка 286: | Строка 293: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Вот пример для метода dikstra | Вот пример для метода <tt>dikstra</tt> | ||
<syntaxhighlight lang="python"> | <syntaxhighlight lang="python"> | ||
Версия от 11:08, 21 января 2012
Внимание! Т.к. модуль активно развивается, статья может содержать устаревшую информацию.
QGIS network-analysis library — библиотека входящая в состав свободной ГИС Quantum GIS, которая:
- может создавать математический граф из географических данных (линейных векторных слоев), пригодный для анализа методами теории графов
- реализует базовые методы теории графов (в настоящее время только метод Дейкстры)
История
Библиотека QGIS network-analysis появилась путем экспорта базовых функций из плагина RoadGraph в отдельную библиотеку.
Начиная с ee19294562, появилась возможность использовать функционал библиотеки в своих расширениях, а также из Консоли Python QGIS.
Применение
Алгоритм применения библиотеки network-analysis можно записать в трех шагах:
- Получить граф из географических данных
- Анализировать граф
- Использовать результат анализа графа в своих целях, например, визуализировать
Получение графа
Первое, что нужно сделать — это подготовить исходные данные, т.е. преобразовать векторный слой в граф. Все дальнейшие действия будут выполняться именно с ним.
В качестве источника графа может выступать любой линейный векторный слой. Узлы линий образуют множество вершин графа. В качестве ребер графа выступают отрезки линий векторного слоя. Узлы имеющие одинаковые координаты образуют единую вершину графа. Таким образом две линии имеющие общий узел оказываются связанными между собой.
В дополнение к этому при построении графа можно привязать к векторному слою любое количество дополнительных точек. Для каждой дополнительной точки будет найдено соответствие - либо ближайшая вершина графа, либо ближайшее ребро. В последнем случае ближайшее ребро будет разбито на две части и будет добавлена общая вершина.
Для назначения свойств ребрам графа могут быть использованы атрибуты векторного слоя и протяженность ребра.
Реализация построения графа из векторного слоя использует шаблон программирования строитель. За построение графа дорог отвечает так называемый Director. В настоящее время бибилотека располагает только одним директором: QgsLineVectorLayerDirector. Директор определяет алгоритм которой строит граф по линейному векторному слою и одним строителем QgsGraphBuilder, его "руками" строиться граф типа QgsGraph. При желании можно реализовать строителя, который будет строить граф, совместимый с такими библиотеками как BGL или networkX.
Для вычисления свойств ребер используется паттерн проектрирования стратегия. Пока в библиотеке реализована только одна стратегия, учитывающая длину маршрута: QgsDistanceArcProperter. При необходимости, можно создать свою стратегию, которая будет учитывать необходимые параметры. Например, в модуле Road graph используется стратегия, вычисляющая время движения по ребру графа на основании длины ребра и поля скорости.
Рассмотрим создание графа более подробно.
Чтобы получить доступ к функциям библиотеки сетевого анализа необходимо импортировать модуль networkanalysis
from qgis.networkanalysis import *
Теперь нужно создать директора
# не использовать информацию о направлении движения из атрибутов слоя, все дороги трактуются как двустронние
director = QgsLineVectorLayerDirector( vLayer, -1, '', '', '', 3 )
# информация о направлении движения находится в поле с индексом 5. Односторонние дороги с прямым направлением
# движения имееют значение атрибута "yes", односторонние дороги с обратным направлением — "1", и соответственно
# двусторонние дороги — "no". По умолчанию дороги считаются двусторонними. Такая схема подходит для использования
# c данными OpenStreetMap
director = QgsLineVectorLayerDirector( vLayer, 5, 'yes', '1', 'no', 3 )
В конструктор директора передается линейный векторный слой, по которому будет строиться граф, а также информация о характере движения по каждому сегменту дороги (разрешенное направление, одностороннее или двустороннее движение). Рассмотрим эти параметры:
- vl — векторный слой, по которому будет строиться граф.
- directionFieldId — индекс поля атрибутивной таблицы, которое содержит информацию о направлении движения. -1 не использовать эту информацию
- directDirectionValue — значение поля, соответствующее прямому направлению движения (т.е. движению в порядке создания точек линии, от первой к последней)
- reverseDirectionValue — значение поля, соответствующее обратному направлению движения (от последней точки к первой)
- bothDirectionValue — значение поля, соответствующее двустроннему движению (т.е. допускается движение как от первой точки к последней, так и в обратном направлении)
- defaultDirection — направление движения по умолчанию. Будет использоваться для тех участков дорог, у которых значение поля directionFieldId не задано или не совпадает ни с одним из вышеперечисленных.
Следующим шагом необходимо создать стратегию назначения свойств ребрам графа
properter = QgsDistanceArcProperter()
Сообщаем директору об используемой стратегии. Один директор может использовать несколько стратегий
director.addProperter( properter )
Теперь создаем строителя, который собственно и будет строить граф заданного типа.
Конструктор QgsGraphBuilder принимает следующие параметры:
- crs — используемая система координат. Обязательный параметр.
- otfEnabled — указывает на использование перепроецирования «на лету». По умолчанию true.
- topologyTolerance — топологическая толерантность. Значение по умолчанию 0.
- ellipsoidID — используемый эллипсоид. По умолчанию "WGS84".
# задана только используемая СК, все остальные параметры по умолчанию
builder = QgsGraphBuilder( myCRS )
Также можно задать одну или несколько точек, которые будет использоваться при анализе. Например так:
startPoint = QgsPoint( 82.7112, 55.1672 )
endPoint = QgsPoint( 83.1879, 54.7079 )
Затем строим граф и «привязываем» к нему точки
tiedPoints = director.makeGraph( builder, [ startPoint, endPoint ] )
Построение графа может занять некоторое время (зависит от количества обектов в слое и размера самого слоя). После построения мы получим граф, пригодный для анализа
graph = builder.graph()
Теперь можно получить индексы наших точек
startId = graph.findVertex( tiedPoints[ 0 ] )
endId = graph.findVertex( tiedPoints[ 1 ] )
Анализ графа
В основе сетевого анализа лежат задача связности вершин графа и задача поиска кратчайших путей. Для решения этих задач в библиотеке network-analysis реализован алгоритм Дейкстры.
Алгоритм Дейкстры находит оптимальный маршрут от одной из вершин графа до всех остальных и значение оптимизируемого параметра. Хорошим способов представления результата выполнения алгоритма Дейкстры является дерево кратчайших путей.
Дерево кратчайших путей - это ориентированный взвешенный граф (точнее дерево) обладающий следующими свойствами:
- Только одна вершина не имеет входящих в нее ребер - корень дерева
- Все остальные вершины имеют только одно входящее в них ребро
- Если вершина B достижима из вершины A, то путь соединяющий их единственный и он же кратчайший (оптимальный) на исходном графе.
Дерево кратчайших путей можно получить пользуясь методом shortestTree или методом dijkstra класса QgsGraphAnalyzer. Рекомендуется пользоваться именно методом dijkstra. Он работает быстрее и в общем случае эффективнее расходует память. Метод shortestTree - может быть полезен, в тех случаях если хотите совершить обход дерева кратчайших путей.
Метод shortestTree создает новый графовый объект (всегда QgsGraph) и принимает три аргумента:
- source — исходный граф
- startVertexIdx — индекс точки на графе (корень дерева)
- criterionNum — порядковый номер используемой стратегии (отсчет ведется от 0).
tree = QgsGraphAnalyzer.shortestTree( graph, startId, 0 )
Метод dijkstra имеет аналогичные параметры. Возвращаемое значение - кортеж из двух массивов. В первом массиве i-ый элемент содержит -1 если это корень дерева или вершина не достижима из корня, в противном случае - индекс дуги входящий в i-ю вершину. Во втором массиве i-ый элемент содержит дистанцию от корня дерева до i-вершины если вершина достижима из корня или максимально большое число которое может хранить тип С++ double (эквивалент плюс бесконечности) если вершина не достижима.
(tree, cost) = QgsGraphAnalyzer.dijkstra( graph, startId, 0 )
Вот так выглядит простейший способ отобразить дерево кратчайших путей для метода shortestTree (только замените координаты начальной точки на свои, а также выделите слой дорог в списке слоёв карты)
from PyQt4.QtCore import *
from PyQt4.QtGui import *
from qgis.core import *
from qgis.gui import *
from qgis.networkanalysis import *
vl = qgis.utils.iface.mapCanvas().currentLayer()
director = QgsLineVectorLayerDirector( vl, -1, '', '', '', 3 )
properter = QgsDistanceArcProperter()
director.addProperter( properter )
crs = qgis.utils.iface.mapCanvas().mapRenderer().destinationCrs()
builder = QgsGraphBuilder( crs )
pStart = QgsPoint( -0.743804, 0.22954 )
tiedPoint = director.makeGraph( builder, [ pStart ] )
pStart = tiedPoint[ 0 ]
graph = builder.graph()
idStart = graph.findVertex( pStart )
tree = QgsGraphAnalyzer.shortestTree( graph, idStart, 0 )
i = 0;
while ( i < tree.arcCount() ):
rb = QgsRubberBand( qgis.utils.iface.mapCanvas() )
rb.setColor ( Qt.red )
rb.addPoint ( tree.vertex( tree.arc( i ).inVertex() ).point() )
rb.addPoint ( tree.vertex( tree.arc( i ).outVertex() ).point() )
i = i + 1
Так для метода dijkstra:
from PyQt4.QtCore import *
from PyQt4.QtGui import *
from qgis.core import *
from qgis.gui import *
from qgis.networkanalysis import *
vl = qgis.utils.iface.mapCanvas().currentLayer()
director = QgsLineVectorLayerDirector( vl, -1, '', '', '', 3 )
properter = QgsDistanceArcProperter()
director.addProperter( properter )
crs = qgis.utils.iface.mapCanvas().mapRenderer().destinationCrs()
builder = QgsGraphBuilder( crs )
pStart = QgsPoint(-0.743804,0.22954)
tiedPoint = director.makeGraph( builder, [ pStart ] )
pStart = tiedPoint[ 0 ]
graph = builder.graph()
idStart = graph.findVertex( pStart )
( tree, costs ) = QgsGraphAnalyzer.dijkstra( graph, idStart, 0 )
for edgeId in tree:
if edgeId == -1:
continue
rb = QgsRubberBand( qgis.utils.iface.mapCanvas() )
rb.setColor ( Qt.red )
rb.addPoint ( graph.vertex( graph.arc( edgeId ).inVertex() ).point() )
rb.addPoint ( graph.vertex( graph.arc( edgeId ).outVertex() ).point() )
Нахождение кратчайших путей
Для получения кратчайшего маршрута между двумя произвольными точками используется следующий подход. Обе точки (начальная A и конечная B) «привязываются» к графу на этапе построения, затем при помощи метода shortestTree или dijkstra получаем дерево кратчайших маршрутов с корнем в начальной точке A. В этом же дереве находим конечную точку B. Начинаем спуск по дереву от точки B к точке А. Алгоритм можно записать так:
- Присвоим Т = B
- Пока Т <> A Цикл
- Добавим в маршрут точку Т
- Берем ребро, которое входит в точку Т
- Находим точку ТТ, из которой это ребро выходит
- Присваиваем Т = ТТ
- Добавим в маршрут точку А
На этом построение маршрута закончено. Вы получили список вершин, в обратном порядке, которые будут посещены при движении по кратчайшему маршруту.
Посмотрите еще раз на дерево кратчайших путей и представьте что вы можете двигаться только против направления стрелочек. Двигайтесь из точки №7. Рано или поздно вы попадете в точку №1 (корень дерева) и не сможете двигаться дальше .
Вот работающий пример для Консоли Python QGIS (только замените координаты начальной и конечной точки на свои, а также выделите слой дорог в списке слоёв карты)
from PyQt4.QtCore import *
from PyQt4.QtGui import *
from qgis.core import *
from qgis.gui import *
from qgis.networkanalysis import *
vl = qgis.utils.iface.mapCanvas().currentLayer()
director = QgsLineVectorLayerDirector( vl, -1, '', '', '', 3 )
properter = QgsDistanceArcProperter()
director.addProperter( properter )
crs = qgis.utils.iface.mapCanvas().mapRenderer().destinationCrs()
builder = QgsGraphBuilder( crs )
pStart = QgsPoint( -0.835953, 0.15679 )
pStop = QgsPoint( -1.1027, 0.699986 )
tiedPoints = director.makeGraph( builder, [ pStart, pStop ] )
graph = builder.graph()
tStart = tiedPoints[ 0 ]
tStop = tiedPoints[ 1 ]
idStart = graph.findVertex( tStart )
tree = QgsGraphAnalyzer.shortestTree( graph, idStart, 0 )
idStart = tree.findVertex( tStart )
idStop = tree.findVertex( tStop )
if idStop == -1:
print 'Path not found'
else:
p = []
while (idStart != idStop ):
l = tree.vertex( idStop ).inArc()
if len( l ) == 0:
break
e = tree.arc( l[ 0 ] )
p.insert( 0, tree.vertex( e.inVertex() ).point() )
idStop = e.outVertex()
p.insert( 0, tStart )
rb = QgsRubberBand( qgis.utils.iface.mapCanvas() )
rb.setColor( Qt.red )
for pnt in p:
rb.addPoint(pnt)
Вот пример для метода dikstra
from PyQt4.QtCore import *
from PyQt4.QtGui import *
from qgis.core import *
from qgis.gui import *
from qgis.networkanalysis import *
vl = qgis.utils.iface.mapCanvas().currentLayer()
director = QgsLineVectorLayerDirector( vl, -1, '', '', '', 3 )
properter = QgsDistanceArcProperter()
director.addProperter( properter )
crs = qgis.utils.iface.mapCanvas().mapRenderer().destinationCrs()
builder = QgsGraphBuilder( crs )
pStart = QgsPoint( -0.835953, 0.15679 )
pStop = QgsPoint( -1.1027, 0.699986 )
tiedPoints = director.makeGraph( builder, [ pStart, pStop ] )
graph = builder.graph()
tStart = tiedPoints[ 0 ]
tStop = tiedPoints[ 1 ]
idStart = graph.findVertex( tStart )
idStop = graph.findVertex( tStop )
( tree, cost ) = QgsGraphAnalyzer.dijkstra( graph, idStart, 0 )
if tree[ idStop ] == -1:
print 'Path not found'
else:
p = [ ]
curPos = idStop;
while curPos != idStart:
p.append( graph.vertex( graph.arc( tree[ curPos ] ).inVertex() ).point() )
curPos = graph.arc( tree[ curPos ] ).outVertex();
p.append( tStart )
rb = QgsRubberBand( qgis.utils.iface.mapCanvas() )
rb.setColor( Qt.red )
for pnt in p:
rb.addPoint(pnt)
Нахождение областей доступности
Актуальная документация
Актуальную документацию всегда можно получить в разделе QGIS network analysis library описания QGIS API.