Создание треугольных сеток на сфере

Эта страница является черновиком статьи.

Два-три предложения.

Постановка задачи

Регулярная...

Генерация сетки в сферическом треугольнике

Процедуру создания на некоторой поверхности сетки треугольников обычно называют триангуляцией. В качестве базы для создания сетки используем некоторый сферический треугольник, заданный координатами своих вершин.

Метод бисекций

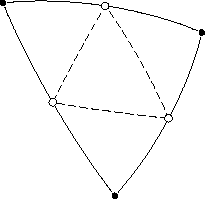
Назовём бисекциями операции деления исходного треугольника на четыре треугольника нового поколения. Собственно термин «бисекция» относится к делению сторон пополам. В середины рёбер вставляются новые вершины (белые точки на рисунках), которые соединяются новыми рёбрами (пунктирные линии), образующими новые треугольники. Следующее поколение получается очередной бисекцией.

В терминах геометрии на сфере задача вставки точек в стороны треугольников решается последовательным решением обратной и прямой геодезических задач. Однако в данном случае гораздо проще использовать векторную алгебру. Пусть концы стороны заданы векторами a и b; тогда средняя точка f вычисляется как их нормированная сумма:

$\mathbf {f} ={\frac {\mathbf {a} +\mathbf {b} }{|\mathbf {a} +\mathbf {b} |}}$

Первая бисекция	Вторая бисекция
Трисекция

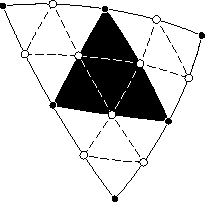
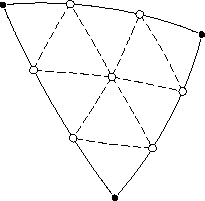
Метод трисекций

Исходный треугольник делится на девять треугольников нового поколения. В результате трисекции каждая сторона делится на три равных отрезка, в концы которых вставляются вершины. Итого шесть новых вершин, и седьмая вставляется в геометрический центр треугольника. Вершины соединяются рёбрами, образующими треугольники.

Проще всего вычислить положение центральной точки g:

$\mathbf {g} ={\frac {\mathbf {a} +\mathbf {b} +\mathbf {c} }{|\mathbf {a} +\mathbf {b} +\mathbf {c} |}}$

где a, b и c — векторы вершин исходного треугольника.

Разделить стороны на три равных отрезка сложнее. Простое решение предлагает утилита PROJ.4 geod:

$ geod +a=радиус_Земли +lat_1=широта_1 +lon_1=долгота_1 +lat_2=широта_2 +lon_2=долгота_2 +n_S=3

где параметры lat_1, lon_1, lat_2, lon_2 задают начало и конец линии, а параметр n_S задаёт число отрезков. Результатом будут широты и долготы четырёх точек, лежащих на равных расстояниях вдоль отрезка.

Сферические многогранники

Сферический многогранник — разбиение сферы дугами больших окружностей на замкнутые области, называемые сферическими многоугольниками. Способы разбиения сферы ничем не ограничены. Однако регулярные построения обычно основаны на симметрии тетраэдра, октаэдра или икосаэдра.

Нас интересуют способы разбиения сферы на треугольники, являющиеся правильными или близкие к правильным, поскольку построенная на каждом таком треугольнике сетка должна быть

Ссылки

• Задачи на сфере: обратная геодезическая задача
• Задачи на сфере: прямая геодезическая задача
• man_geod – PROJ.4
• Spherical polyhedron