Краткое введение в MaxEnt

Эта страница является черновиком статьи.

Автор: Стивен Филлипс (Steven Phillips), AT&T Research

Перевод: Максим Дубинин и надеюсь кто-то еще :)

Это руководство представляет из себя краткое введение в использование программы MaxEnt предназначенной для моделирования географического распространения видов методом максимальной энтропии. Авторы руководства Стивен Филлипс (Steven Phillips), Миро Дудик (Miro Dudik) и Роб Шапир (Rob Schapire), благодаря поддержке AT&T Labs-Research, Университета Принстона и Центр биоразнообразия и охраны природы Американского музея естественной истории (Center for Biodiversity and Conservation, American Museum of Natural History). Более подробное описание теории энтропийного моделирования и описание использованных наборов данных и типов статистического анализ можно найти в следующих статьях:

Steven J. Phillips, Robert P. Anderson and Robert E. Schapire, Maximum entropy modeling of species geographic distributions. Ecological Modelling, Vol 190/3-4 pp 231-259, 2006.

Вторая статья, описывающая относительно новую функциональность ПО Maxent:

Steven J. Phillips and Miroslav Dudik, Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation. Ecography, Vol 31, pp 161-175, 2008.

Используемые данные о параметрах окружающей среды включают климатические и высотные данные по Южной Америке, а также слой потенциальной растительности. Моделируемый вид – Бурогорлый ленивец (Bradypus variegates). Это руководство подразумевает, что все учебные данные расположены в той же папке, где расположен сам Maxent; если это не так – добавляйте свой путь (например, c:\data\maxent\tutorial) к используемым здесь названиям файлов.

Словарь

feature - объект

product feature - производные объекты

hinge features - петлевые объекты

presence - присутствие

absence - отсутствие

response curve - кривая зависимости (кривая отклика)

predicted suitability - предсказанное качество

threshold features - пороговые объекты

step function - ступенчатая функция

piece-wise linear function - кусочно-линейная функция

sigmoid function - сигмоидная функция

additive function - аддитивная функция

Maxent exponent - экспонента Maxent

overfitting - излишнее соответствие, притягивание

Начало

Загрузка

Программное обеспечение включает файл jar, maxent.jar, который может быть запущен на любом компьютере на котором есть версия Java 1.4 или выше. Сам Maxent и документация можно загрузить по адресу www.cs.princeton.edu/~schapire/maxent; Java runtime environment можно получить по адресу http://java.sun.com/javase/downloads. Если вы используете Microsoft Windows (как здесь подразумевается), то нужно также загрузить файл maxent.bat и сохранить его в той же папке, где хранится maxent.jar. На веб сайте есть файл “readme.txt”, где содержатся инструкции по установке программы.

Запуск

Если вы используете Microsoft Windows, просто щелкните на файле maxent.bat. Если у вас другая операционная система введите в командной строке "java -mx512m -jar maxent.jar" (где "512" можно заменить на количество мегабайт памяти которое вы хотите выделить для программы). Появится такое окно:

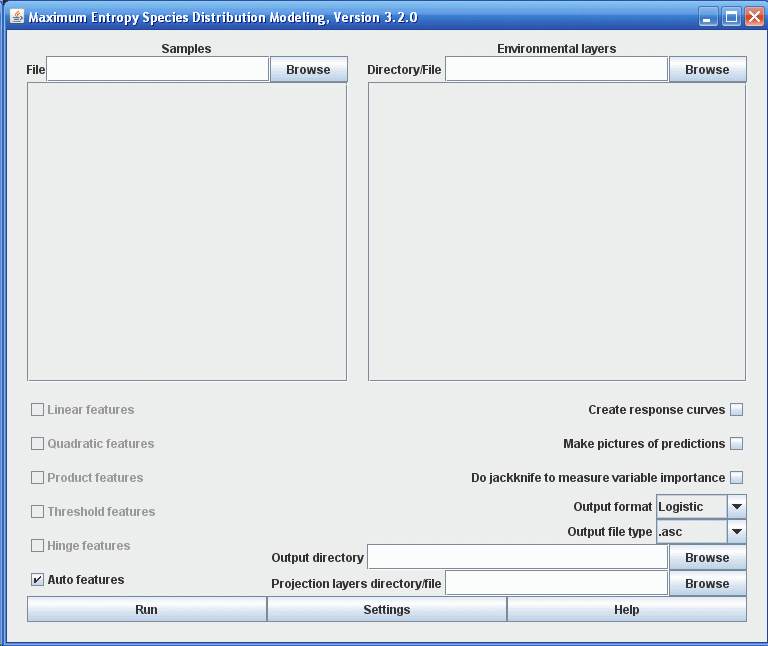
Чтобы запустить процесс, нужно предоставить файл содержащий точки встреч (“samples”), папку содержащую слои с параметрами окружающей среды и выходную папку. В нашем случае точки встреч находятся в файле “samples\bradypus.csv”, слои параметров среды в папке “layers” и выходные результаты будут сохранятся в папке “outputs”. Вы можете вводить эти значения вручную или использовать проводник. Когда вы ищете переменные среды, помните, что нужна папка, которая их содержит, а не сами файлы. После ввода необходимых параметров окно программы должно выглядеть следующим образом:

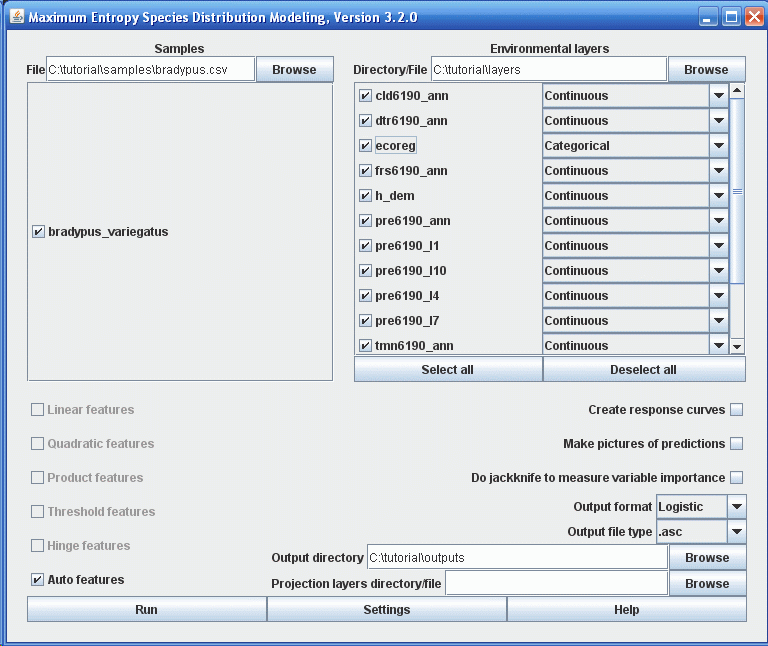
Файл “samples\bradypus.csv” содержит находки в формате .csv. Несколько первых строк выглядят следующим образом:

species,longitude,latitude
bradypus_variegatus,-65.4,-10.3833
bradypus_variegatus,-65.3833,-10.3833
bradypus_variegatus,-65.1333,-16.8
bradypus_variegatus,-63.6667,-17.45
bradypus_variegatus,-63.85,-17.4

В файле находок может быть несколько видов, в этом случае будет сгенерировано больше результатов, кроме Bradypus. Координаты находок могут находиться в системах координат отличных от широта/долгота, но в них должны быть и находки и слои данных. В файле находок координата X (в нашем случае долгота) должна распологаться до координаты Y (широта). Если в данных есть дубликаты (несколько записей для одного и того же вида в одной и той же ячейке), то по умолчанию они удаляются; это поведение можно отключить нажав на кнопку “Settings” и отключив “Remove duplicate presence records”.

Папка “layers” содержит растровые слои данных в формате ESRI .asc, каждый из которых описывает определенный параметр окружающей среды. Все растры должны иметь одинаковый географический охват и размер ячейки (т.е. заголовки файлов ascii должны быть строго одинаковыми). Одна из наших переменных “ecoreg” - категорийная, она указывает класс потенциальной растительности. Категории должны быть указаны цифрами, а не буквами или словами. Необходимо указать программе, какие из переменных являются категорийными, так как показано на иллюстрации выше.

Запуск модели

Просто нажмите кнопку “Run”. Появится индикатор прогресса описывающий текущие шаги выполняемые программой. После загрузки слоев и иннициализации, прогресс тренировки модели максимальной энтропии показывается так:

Прирост (gain) тесно связан с Deviance, которая является мерой качества модели (статистическим критерием) используемой в обобщенных аддитивных и линейных моделях. Прирост начинается с 0 и асимптотически растет в процессе расчета. При расчете Maxent генерирует распределение вероятности ячеек растра, начиная с равномерного распределения и постепенно улучшая соответствие модели данным. Прирост определяется как средняя лог-вероятность образцов присутствия, минус константа, которая делает равным нулю прирост равномерного распределения. В конце прохода, прирост показывает насколько сильно модель сконцентрирована вокруг образцов присутствия; например, если прирост = 2, это означает, что среднее правдоподобие образцов присутствия в exp(2) ≈ 7.4 раз выше, чем у случайных ячеек фона. Отметьте, что Maxent не расчитывает “вероятность присутствия” напрямую. Вероятность, которую Maxent назначает каждой ячейке обычно очень мала, так как значения всех ячеек растра должны в сумме быть равны 1 (мы вернемся к этому моменту, когда будем сравнивать выходные форматы).

После запуска модели будет создано несколько выходных файлов, основным является “bradypus.html”. В конце этого файла также содержатся ссылки на другие результаты:

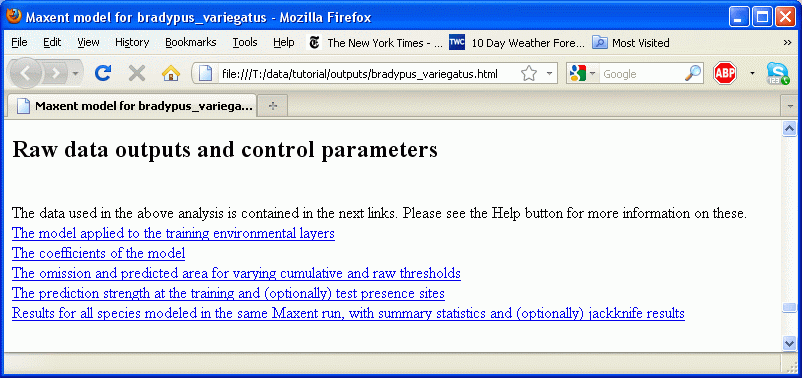
Просмотр предсказания

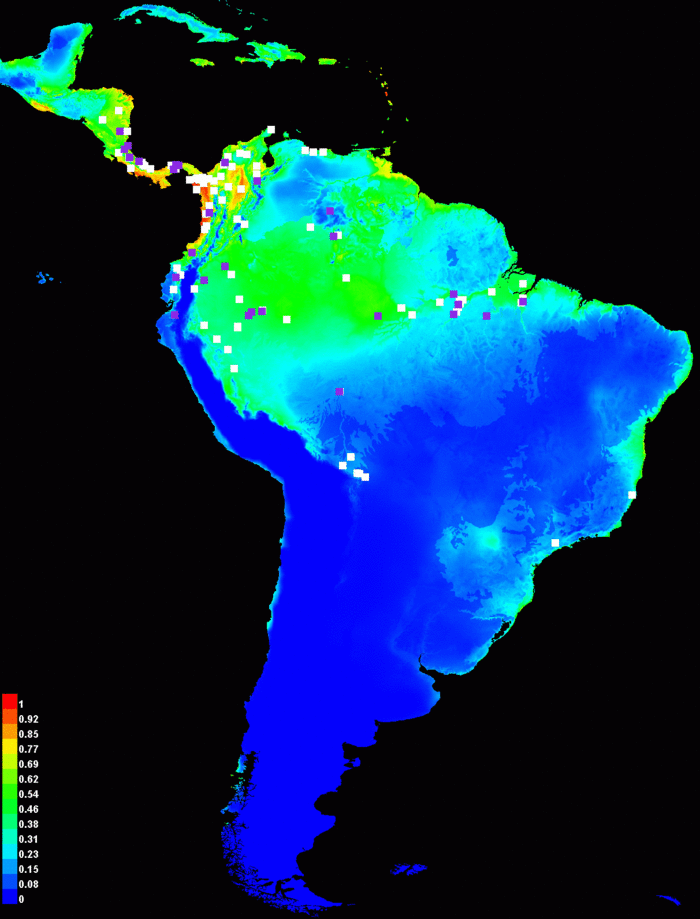
По умолчанию, выходные результаты в формате html содержат графический результат модели примененной к заданным параметрам окружающей среды:

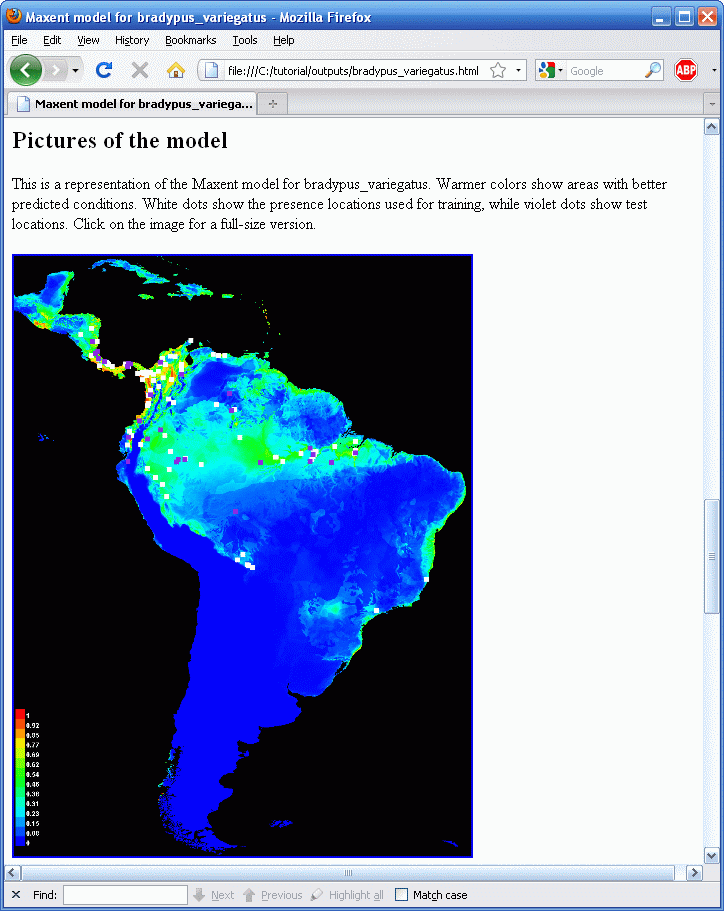
Результирующее изображение цветами показывает расчетную вероятность что условия для находки подходящие, красным показывается высокая вероятность подходящих условий для вида, зеленым – условия похожие на те, в которых находится вид, оттенки синего – маловероятные условия. Для нашего Bradypus можно отметить, что подходящие условия предсказываются быть высоковероятны на протяженности большей части низин Центральной Америки, влажных низин северозапада Южной Америки, в бассейне Амазонки, на Карибских островав и большей части Атлантических лесов юго-восточной Бразилии. Графическое представление модели это простой графический файл (.png), по нему можно щелкнуть или открыть в любом графическом редакторе. Если вам нужно скопировать эти данные или открыть их с помощью другого ПО, вам нужно найти файлы .png в папке “plots” которая создается в папке с результатами работы.

Тестовые точки представляют из себя случайную выборку из набора находок. Эта же случайная выборка используется каждый раз при запуске Maxent на одном и том же наборе данных, если не выбрана опция генерации случайной выборки “random seed” в установках. Альтернативно, тестовые данные могут находиться в отдельным файлом и указаны в опции “Test sample file” в настройках.

Выходные форматы

Maxent поддерживает три выходных формата значений модели: исходный, кумулятивный и логистический. Первый, исходный формат представляет из себя саму экспоненциальную модель Maxent. Второе, кумулятивное значение соответствующее исходному значению r – процент распределения Maxent с исходным значением в большинстве r. Кумулятивный выходной формат лучше интерпретировать как предсказываемый уровень омиссии (пропуска): если мы установим кумулятивный порог c, результирующее бинарное предсказание будет иметь уровень омиссии c% при выборке из самого распределения Maxent, и мы можем предсказать такой же уровень омиссии для выборки из распределения вида. Третий формат, если c является экспоненциалом энтропии распределения Maxent, то логичстическое значение соответствующее исходному значению r расчитывается как c·r/(1+c·r). Это логистическая функция, так как исходное значение - экспоненциальная функция переменных среды. Три выходных формата монотонно связаны, но разным образом масштабированы и имеют разную интерпретацию. Выходной формат по умолчанию – логистический, его интерпретировать проще всего: он дает оценку вероятности находки между 0 и 1. Отметьте, что вероятность находки зависит от того, как собирались данные, например размера участка (для мобильных видов), время наблюдения; логистическое значение оценивает вероятность находки подразумевая, что сэмплинг таков, что типичные локации имеют вероятность находки 0.5. Иллюстрация модели Bradypus выше использует логистический формат. Для сравнения, исходный формат даст такое изображение:

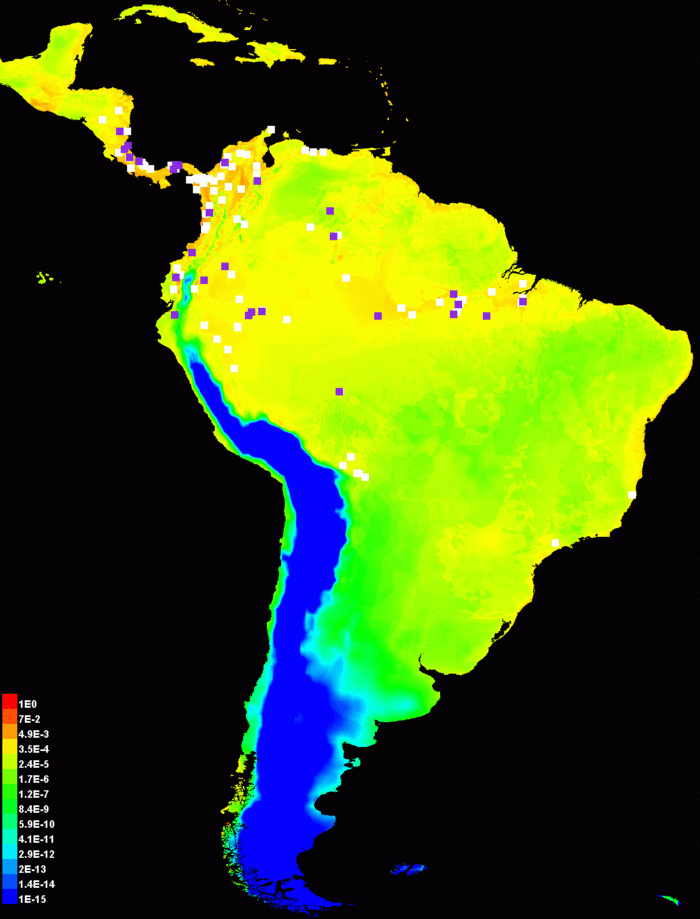
Обратите внимание, что используется логарифмическая шкала цветов. Линейная шкала была бы представлена в основном синими цветами с несколькими красными пикселами (убедиться в этом можно отключив пункт “Logscale pictures” в панели Settings) так как исходные данные обычно имеют небольшое число пунктов с относительно большими значениями – это можно рассматривать как артефакт того, что сырые выходные данные имеют экспоненциальное распространение.

Выбор кумулятивного выходного формата даст следующую картину:

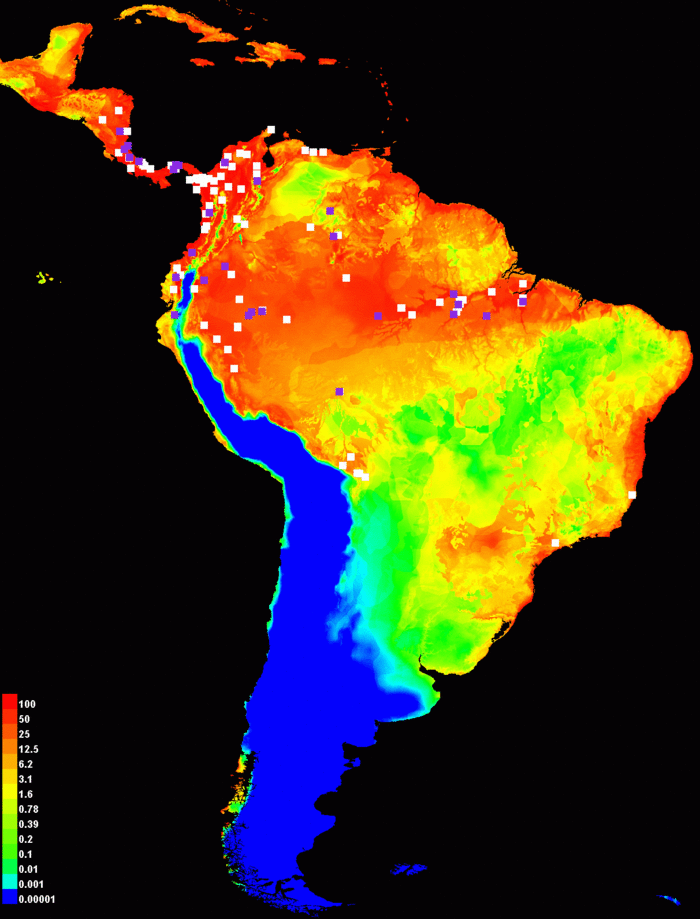
Так же, как и с сырыми выходными данными, мы использовали логарифмическую шкалу для расцветки для того чтобы подчеркнуть различия между небольшими значениями. Кумулятивные выходные данные могут быть интерпретированы как предсказание подходящих условий для вида выше порога с примерным диапазоном 1-20 (цветовой градиент от желтого до оранжевого на иллюстрации), в зависимости от подходящего уровня предсказанной омиссии.

Статистический анализ

Цифра “25”, которую мы ввели как процент случайных тестовых данных (“random test percentage”) говорит программе, чтобы она случайным образом отобрала 25% находок и отложила их в сторону для тестирования. Это позволяет произвести статистический анализ точности. Часто для анализа используется порог для бинаризации предсказания, условия считаются пригодными если предсказание выше порога и непригодным если ниже. Первый график показывается как меняется омиссия и предсказанная территория по тестовым и тренировочным точкам в зависимости от кумулятивного порога:

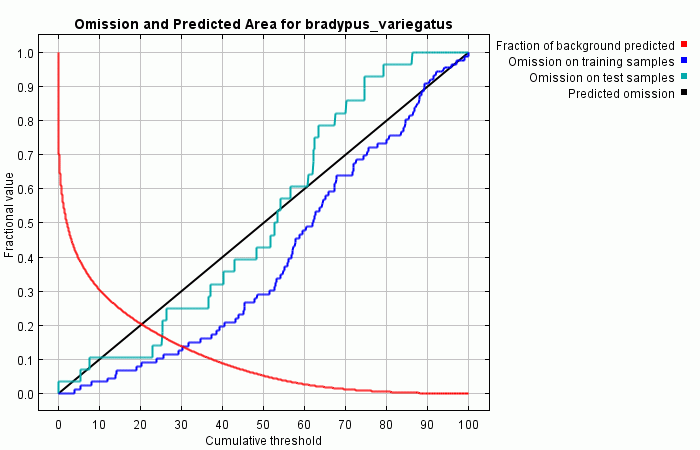
По этому графику можно сказать, что омиссия по тестовым точкам довольно хорошо совпадает с предсказанной динамикой омиссии, рассчитанной для тестовых данных полученных из самого распределения Maxent. Предсказанная омиссия является прямой линией по определению кумулятивного формата. В некоторых ситуациях, линия омиссии по тестовым точкам может лежать ниже предсказанной линии, обычное объяснение этому может заключаться в том, что тестовые и тренировочные данные не независимы, если они например получены из общего автокоррелированного набора данных о находках.

Следующий график (см. ниже) показывает receiver operating curve для тренировочных и тестовых данных. Приведена площадь под кривой ROC (AUC); если есть тестовые данные, ниже на странице отчета можно увидеть стандартную ошибку AUC на тестовых данных.

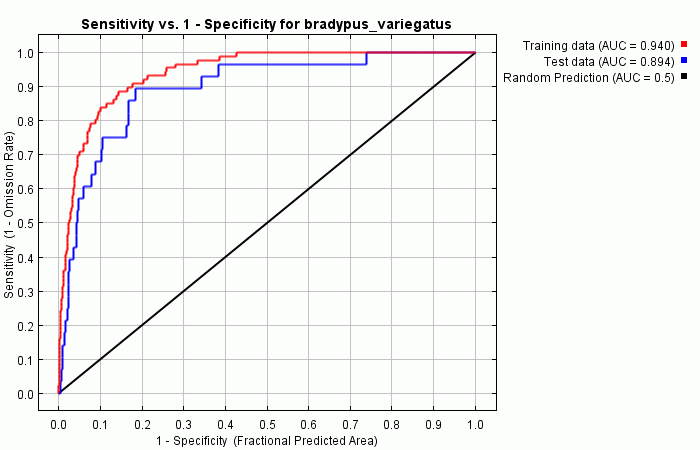
Красный и синий график будут совпадать, если для тренировки и тестирования используются одни и те же данные. Если данные разделены на две части, одна из которых для тренировки, а вторая для тестирования, то красная кривая (тренировка) показывает значение AUC выше, чем синяя (тестирование). Красная кривая показывает насколько хорошо модель описывает тренировочные данные (“fit”). Синяя линия показывает насколько хорошо модель описывает тестовые данные и является реальным тестом предсказательной способности модели. Черная линия показывает ситуацию которую можно было бы ожидать, если бы модель была не лучше случайной. Если синяя линия находится ниже черной, это означает, что модель хуже, чем случайная. Чем ближе к верхнему левому углу находится синяя линия, тем лучше модель предсказывает находки содержащиеся в тестовой выборке. Подробная начальную информацию об AUC можно найти в: Fielding, A.H. & Bell, J.F. (1997) A review of methods for the assessment of prediction errors in conservation presence/absence models. Environmental Conservation 24(1): 38-49. Поскольку у нас есть только данные о находках, но нет данных об отсутствии, вместо ошибки комиссии (доля отсутствующих предсказанная как встречи) используется “fractional predicted area” (доля от площади территории исследования занимаемая встречами. С обсуждением выбора этого показателя можно ознакомиться в статье в Ecological Modelling упоминаемой на первой странице этого руководства. Важно отметить, что значения AUC имеют тенденцию быть выше для видов с небольшими участками относительно территории исследования описываемой слоями данных. Это не обязательно означает, что модель лучше; это артефакт показателя AUC.

Если есть данные для тестирования, программа автоматически подсчитает статистическую значимость предсказания используя биномиальный тест на омиссию. Для Bradypus получится:

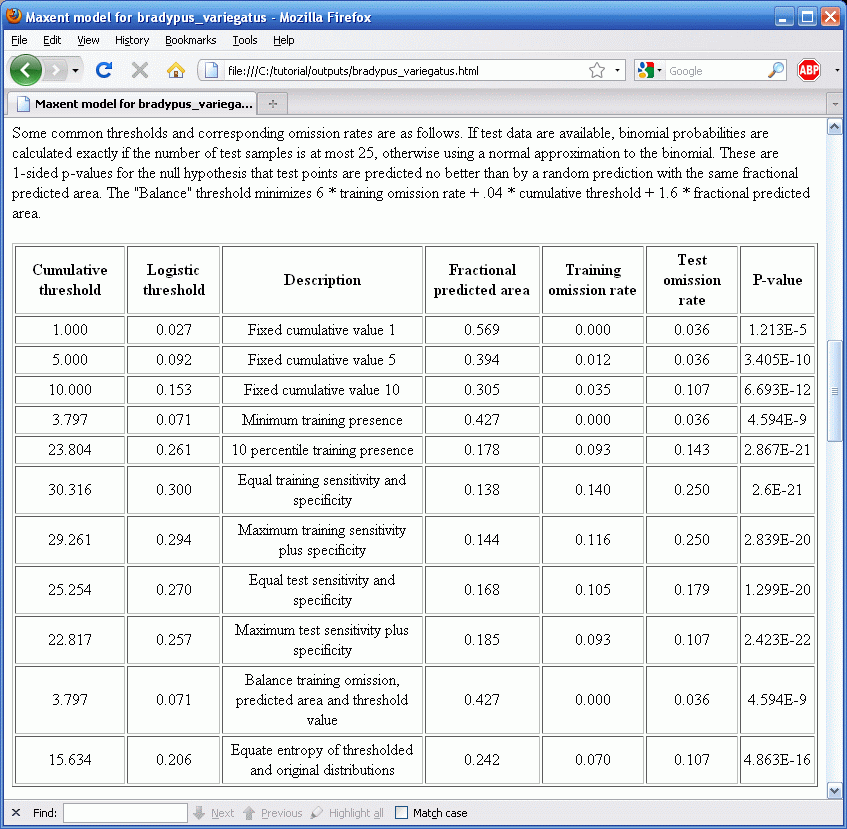
Подробную информацию по биномиальной статистике можно найти в статье в Ecological Modelling.

Какие переменные имеют больший вес?

Естественное применение моделирования – попытка ответить на вопрос, какая из переменных более важна для вида? Существует несколько способов дать ответ на этот вопрос с помощью Maxent.

В процессе тренировки модели Maxent, она отслеживает какие переменные среды вносят вклад в построение модели. Каждый шаг алгоритма Maxent увеличивает прирост модели изменяя коэффициент для одной feature; программа назначает увеличение прироста той переменной или переменным среды, от которой зависит feature. В конце процесса тренировки происходит пересчет приростов в проценты и получается средняя колонка в таблице:

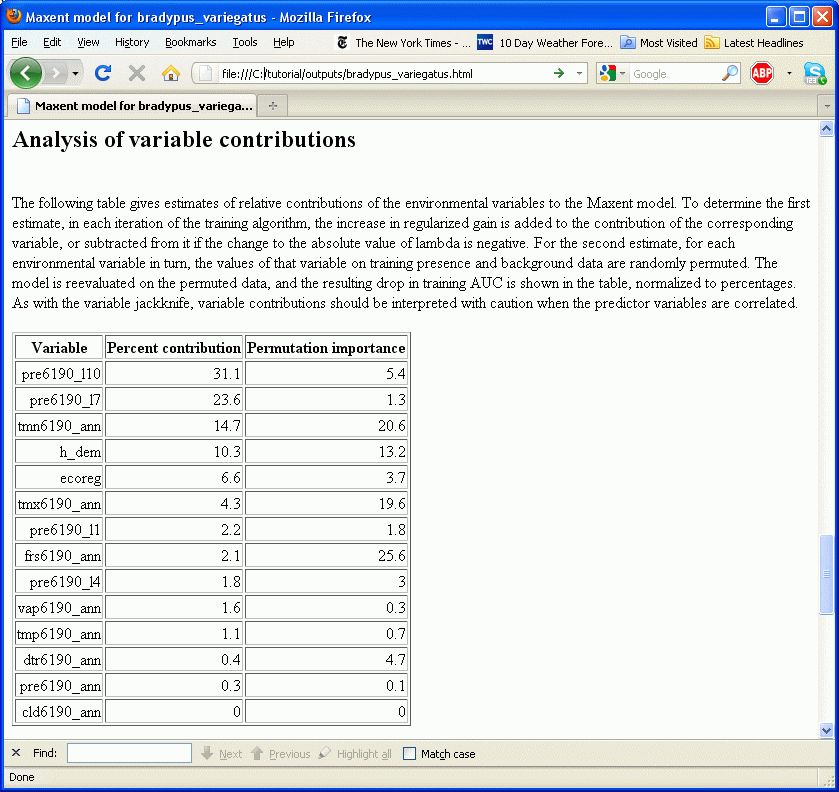
Эти процентные вклады определяются только эвристически и зависят от конкретного пути по которому пошел код Maxent чтобы достичь оптимального решения и другой алгоритм мог бы придти к тому же решению используя другой путь, который бы закончился другими процентами вклада. Дополнительно, если присутствуют сильно скоррелированные переменные, вклад должен интерпретироваться с осторожностью. В нашем примере с Bradypus, годовые осадки сильно скоррелированы с осадками в Октябре и Июле. Хотя таблица выше показывает, что Maxent использовал осадки Октябрь больше чем любую другую переменную и вообще не использовал годовые осадки это не обязательно означает, что осадки в Октябре гораздо более важны для вида чем годовые осадки.

Правая колонка в таблице показывает второй показатель вклада переменной – важность при пермутации (permutation importance). Этот показатель зависит только от окончательной модели, а не пути, который был пройден, чтобы ее получить. Вклад каждой переменной определяется посредством случайного изменения значений этой переменной у тренировочных точек (и находок и фона) и измерения уменьшения тренировочной AUC. Сильное уменьшение свидетельствует о том, что модель сильно зависит от этой переменной. Значения нормализованы, чтобы показывались в процентах.

Альтернативной оценкой важности переменной может быть jackknife-тест, который можно провести включив переключатель “Do jackknife to measure variable important” (Производить jackknife-тест для измерения важности переменной). После нажатия кнопки “Run” (Запуск) создается набор моделей. Каждая переменная исключается в свою очередь и модель создается с остальными переменными. Затем модель создается только с этой переменной. Дополнительно, создается модель со всеми переменными, как раньше. Результаты jackknife-тестов будут показываться в файле “bradypus.html” в виде трех столбчатых диаграмм, первая из них показана ниже.

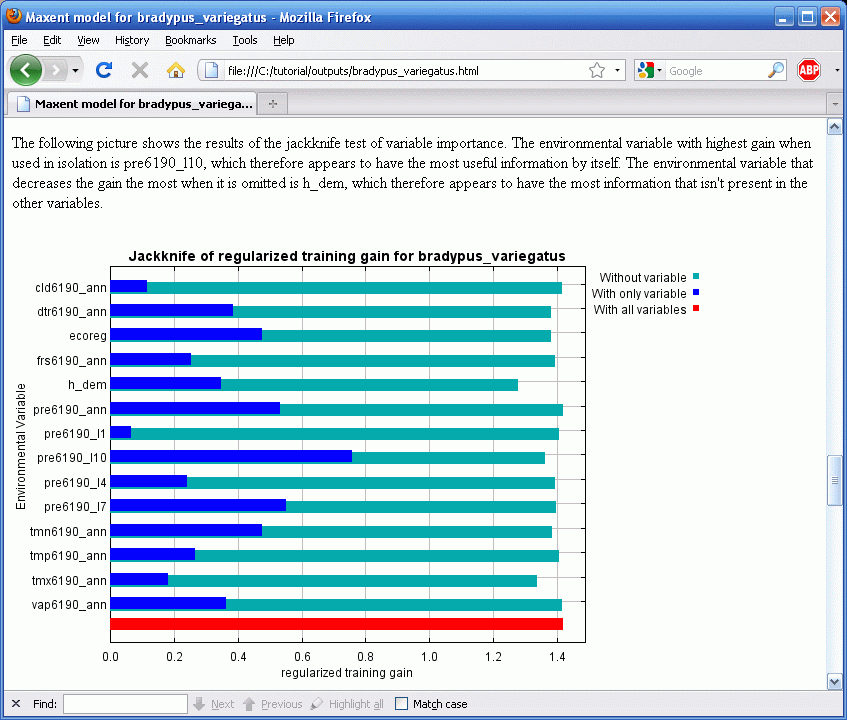
На примере видно, что если Maxent использует только pre6190_l1 (среднее количество осадков в январе) то прироста почти нет, так что, сама по себе эта переменная бесполезна для моделирования распространения Bradypus. С другой стороны, осадки в октябре (pre6190_l10) достаточно хорошо описывают данные. Переключаясь на голубые столбцы, можно отметить, что ни одна из переменных не содержит значительного количества уникальной информации, которая бы не содержалась в других переменных, потому что выключение каждой переменной не привело к значительному уменьшению прироста.

В файле bradypus.html также находятся еще две диаграммы результатов jackknife-теста, показывающих прирост для тестовых данных или AUC, см. ниже:

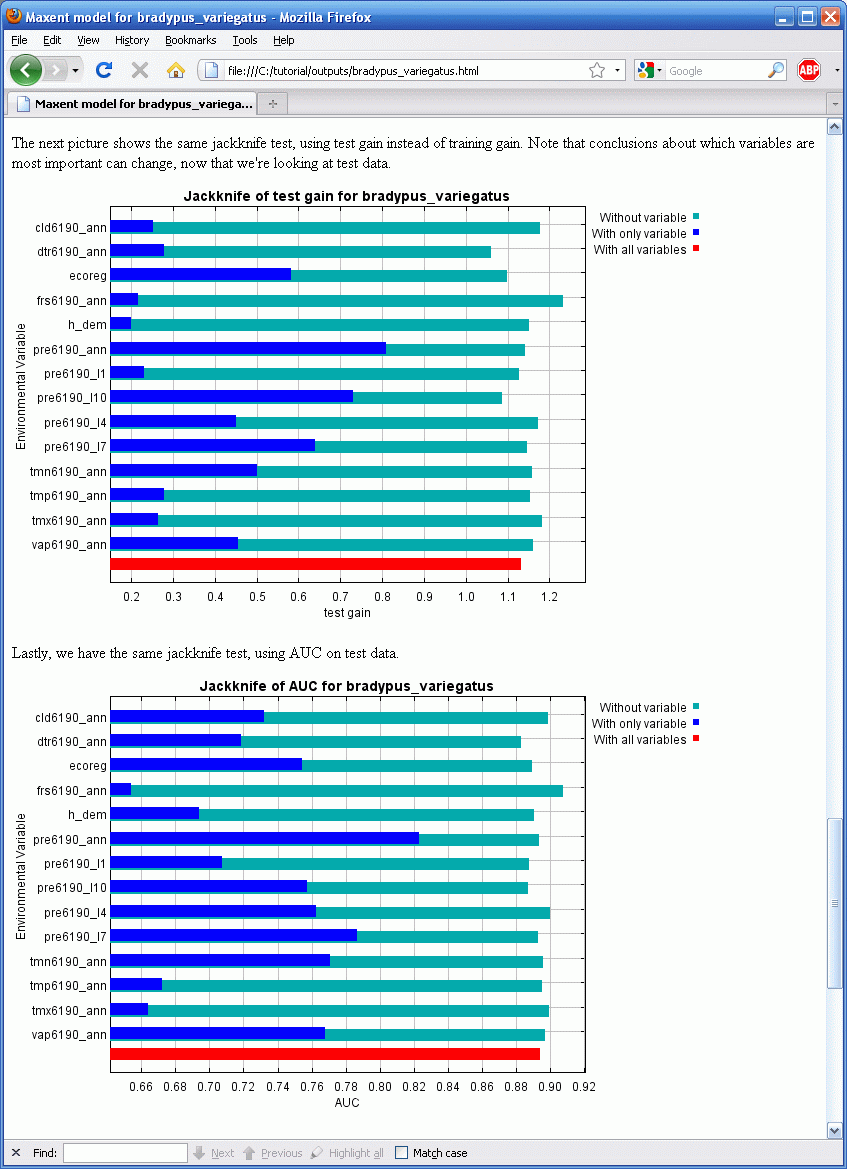
Сравнение диаграмм может быть весьма полезным. Диаграмма AUC показывает, что годовые осадки – переменная наиболее эффективно предсказывающая распределение точек находок которые были выделены в тестовый набор данных, если эффективность предсказания измеряется используя AUC, несмотря на то, что она почти совсем не используется для построения модели когда используются все переменные. Относительная важность годовых осадков также достаточно велика судя по диаграмме прироста по тестовым данным, по сравнению с тренировочными. Дополнительно, эти две диаграммы показывают, что некоторые из светло-голубых столбцов (особенно для месячных осадков) длиннее чем красный столбец, что говорит о том, что предсказательная сила модели увеличивается если эти переменные не используются.

Это говорит нам о том, что переменные месячных осадков помогают Maxent хорошо описать тренировочные данные, но годовые осадки лучше генерализуют, показывая сравнительно лучший результат для отложенных тестовых данных. Другими словами, модели созданные с месячными осадками являются менее переносимыми. Это важно, если нашей целью является перенос модели, например применение ее к будущим климатическим переменным с тем, чтобы оценить будущее распространение вида при условии изменения климата. То, что месячные значения осадков являются менее переносимыми – логично: вероятно, что подходящие местообитания для Bradypus будут зависеть не от точных значений осадков в конкретный месяц, а от общих значений и, возможно, периодичности дождей и отсутствия сухих периодов. При моделировании на континентальном уровне весьма вероятны сдвиги в точном времени сезонных осадков, которые будут влиять на месячные осадки, но не на подходящие условия для Bradypus.

В целом, лучше использовать переменные которые будут вероятнее напрямую связаны с моделируемым видом. Например, вебсайт Worldclim (www.worldclim.org) предоставляет переменные “BIOCLIM”, включающие прозводные, такие как “осадки в четверть с наибольшим их количеством ”, а не просто месячные значения.

Последнее замечание о результатах jackknife-теста: диаграмма прироста с тестовыми данными показывает, что модель созданная только с осадками в январе (pre6190_l1) имеет отрицательный прирост. Это означает, что модель хуже, чем нулевая (т.е., a uniform distribution) дял предсказания распространения находок отложенных для тестирования. Это предоставляет дальнейшие данные о том, что значения месячных осадков не самый лучший выбор для предсказания.

Как предсказание зависит от переменных?

Теперь нажмите на “Create response curves”, отключите jackknife, и перезапустите расчеты. В результате к “bradypus.html” добавится еще одна секция:

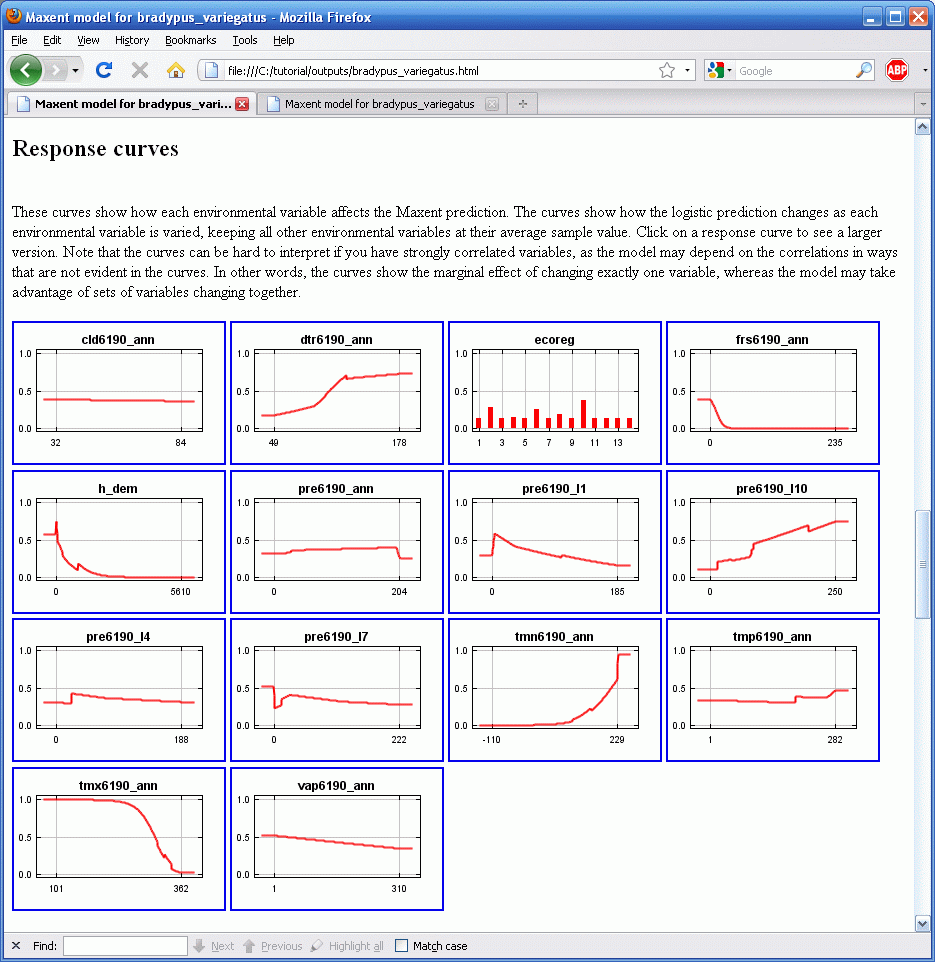
Каждая из картинок является ссылкой, при нажатии на которую откроется полная версия графика, сами файлы в формате .png находятся в папке “plots”. Изучение vap6190_ann показывает, что отклик имеет небольшие значения при значениях vap6190_ann в диапазоне 1-200, и высокие при значениях в диапазоне 200-300. Значение на оси Y это предсказанная вероятность подходящих условий, в логистическом формате вывода, при том что все остальные переменные становлены в средние значения расчитанные по всему набору находок (presence localities).

Отметьте, что если переменные среды скоррелированы, как в нашем примере, кривые отклика могут быть противоречивы. Например, если две сильно коррелирующие переменные имеют кривые отклика которые ведут себя совершенно по разному, то совокупный эффект двух переменных может быть очень мал для большинства пикселей. Другой пример, из примера видно, что предсказанное качество (predicted suitability) отрицательно коррелирует с годовыми осадками (pre6190_ann), если все другие переменные константны. Другими словами, как только эффект всех других переменных учтен, эффект увеличения годовых осадков будет выражаться в уменьшении предсказанного качества местообитания. Однако, годовые осадки сильно коррелируют с ежемесячными осадками, так что на самом деле мы вряд ли сможем зафиксировать ежемесячные значения и менять годовые. Поэтому программа создает два набора кривых отклика, во втором наборе каждая кривая приводится для случая, когда модель построена используя только саму переменную и другие переменные в нее не вводятся:

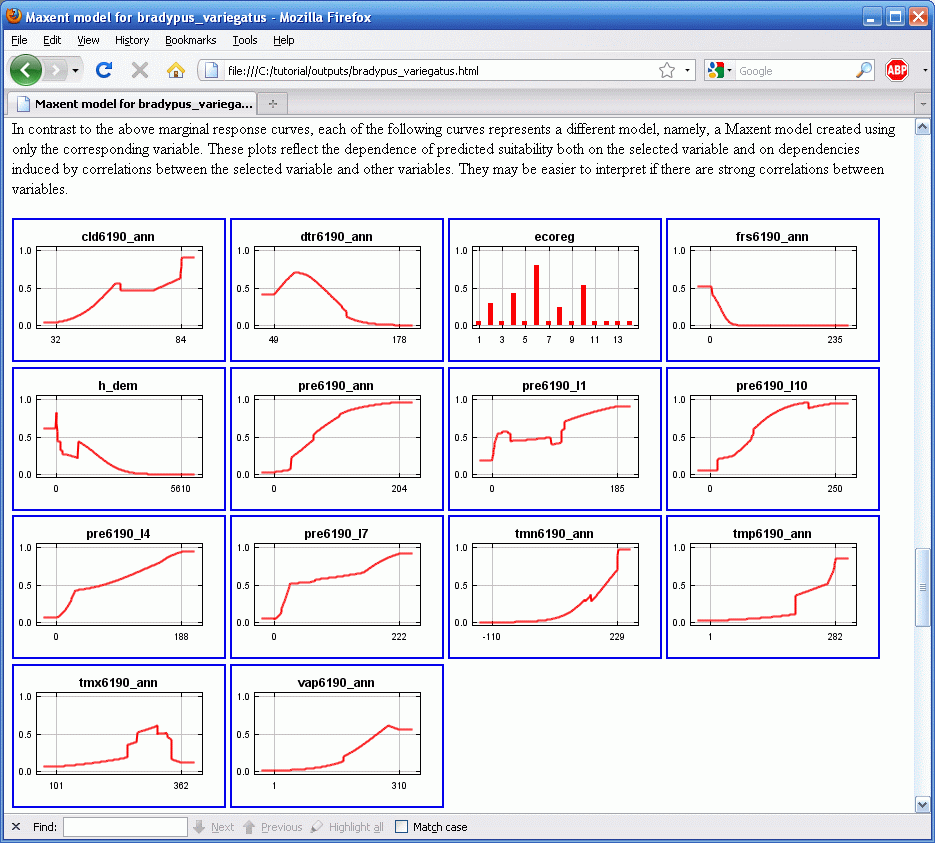
По сравнению с откликом на годовые осадки в первом наборе, во втором мы видим, что предсказанное качество в целом растет с ростом годовых осадков.

Типы объектов and кривые зависимостей

Кривые зависимостей позволяют нам увидеть разницу между различными типами объектов. Отключите авто-объекты (“Auto features”), оставьте выбранными только пороговые объекты (“Threshold features”), и снова нажмите кнопку запуска (“Run”). Посмотрите на результирующий профиль функции – она выгрядит как набор ступенек, например так для переменной 6190_l10:

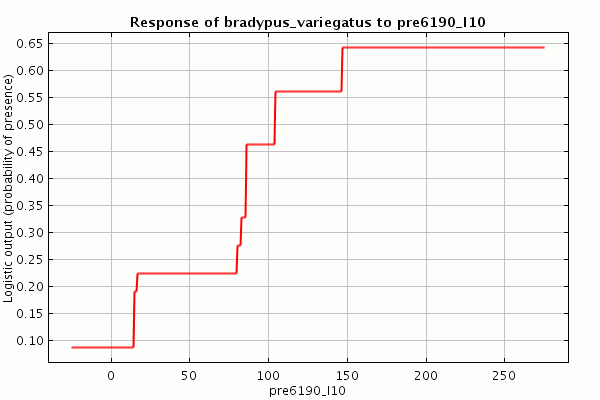
Теперь попробуйте тоже самое используя только петлевые объекты («hinge features»), результат будет выглядеть примерно так:

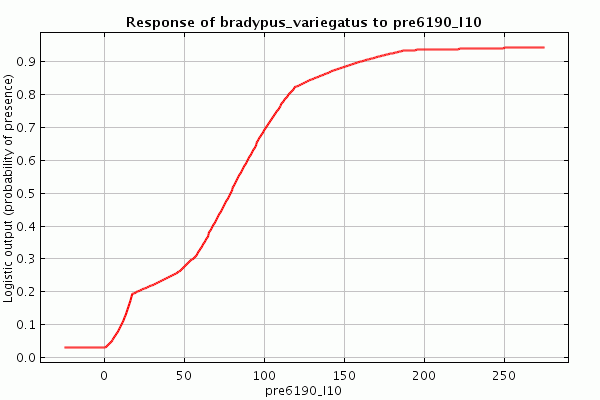
Общий контур двух профилей похож, но в деталях они разные, так как разные типы объектов позволяют разные возможные формы кривых зависимостей. Экспонента в модели Maxent является суммой объектов и сумма пороговых объектов это всегда ступенчатая функция, так что логистический результат - тоже ступенчатая функция (также как сырой и кумулятивный результат). Для сравнения, сумма петлевых объектов - всегда кусочно-линейная функция, так что если используются только петлевые объекты, экспонента Maxent является кусочно линейной. Это объясняет последовательность соединенных линейных сегментов во второй кривой зависимости приведенной выше. (Отметьте, что линии слегка кривые, особенно там где значения переменной близки к экстремальным; это происходит потому что логистический результат применяет сигмоидную функцию к экспоненте Maxent.) Использование всех видов объектов (по умолчанию, если достаточно данных) позволяет точно моделировать даже сложные зависимости. Более подробное объяснение различных видов объектов доступно в справке программы (кнопка help).

Интерактивное изучение результатов предсказания: инструмент Explain (объяснение)

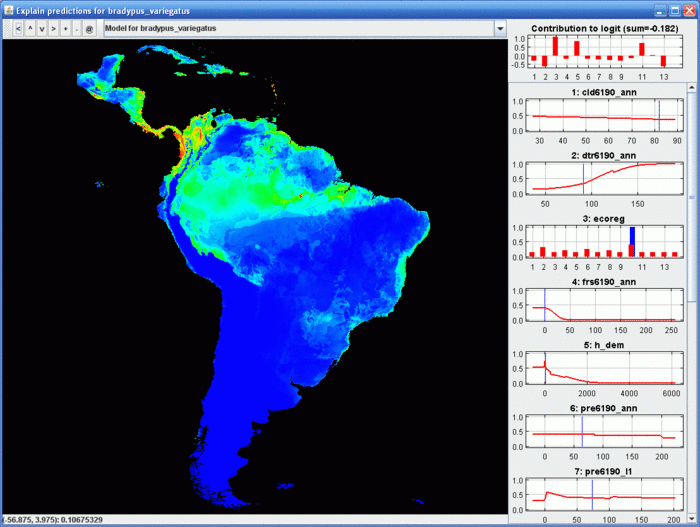
Этот интерактивный инструмент позволяет изучить, как предсказание Maxent связано со значениями предикторов в любом месте территории исследования. Щелкнув на точку на карте можно посмотреть на ее положение на кривой отклика. Верхний правый график показывает каков вклад каждой переменной в логит предсказания (logit of the prediction) (наведя курсор на одну из колонок можно увидеть имя переменной и значение в цифрах). Изучив вклад в логит, можно сказать, как разные переменные влияют на предсказание в разных частях территории исследования.

Инструменту нужно, чтобы модель была аддитивная (без взаимодействий между переменными) поэтому использовать инструмент можно только на результатах полученных без product features. Так же, компьютеру может понадобится больше памяти, чтобы держать в ней одновременно все предикторы. Если вы прогоните модель без product features, после главной иллюстрации работы модели появится ссылка, нажав на которую можно будет запустить инструмент.

Формат SWD

Еще один формат который может оказаться полезным, особенно если вы имеете дело с предикторами очень большими по объему. Для простоты этот формат называется образцы с данными (“samples with data”) или SWD. SWD-версия файла Bradypus называется “bradypus_swd.csv” и его содержание начинается так:

species,longitude,latitude,cld6190_ann,dtr6190_ann,ecoreg,frs6190_ann,h_dem,pre6190_ann,pre6190_l10,pre6190_l1,pre6190_l4,pre6190_l7,tmn6190_ann,tmp6190_ann,tmx6190_ann,vap6190_ann
bradypus_variegatus,-65.4,-10.3833,76.0,104.0,10.0,2.0,121.0,46.0,41.0,84.0,54.0,3.0,192.0,266.0,337.0,279.0
bradypus_variegatus,-65.3833,-10.3833,76.0,104.0,10.0,2.0,121.0,46.0,40.0,84.0,54.0,3.0,192.0,266.0,337.0,279.0
bradypus_variegatus,-65.1333,-16.8,57.0,114.0,10.0,1.0,211.0,65.0,56.0,129.0,58.0,34.0,140.0,244.0,321.0,221.0
bradypus_variegatus,-63.6667,-17.45,57.0,112.0,10.0,3.0,363.0,36.0,33.0,71.0,27.0,13.0,135.0,229.0,307.0,202.0
bradypus_variegatus,-63.85,-17.4,57.0,113.0,10.0,3.0,303.0,39.0,35.0,77.0,29.0,15.0,134.0,229.0,306.0,202.0

Такой файл может использоваться вместо обычного файла образцов. Разница только в том, что при использовании SWD программе не нужно смотреть в слои предикторов (ASCII файлы) чтобы получить значения переменных в точках, вместо этого она считывает эти значения прямо из таблицы. Слои предикторов в этом случае используются только для того, чтобы считать данные о “фоновых” пикселях - т.е. пикселях, где вид (явление) не было обязательно детектировано. На самом деле, фоновые пиксели тоже могут быть заданы как файл в формате SWD. Файл “background.csv” содержит 10,000 фоновых точек. Несколько первых записей выглядят так:

background,-61.775,6.175,60.0,100.0,10.0,0.0,747.0,55.0,24.0,57.0,45.0,81.0,182.0,239.0,300.0,232.0
background,-66.075,5.325,67.0,116.0,10.0,3.0,1038.0,75.0,16.0,68.0,64.0,145.0,181.0,246.0,331.0,234.0
background,-59.875,-26.325,47.0,129.0,9.0,1.0,73.0,31.0,43.0,32.0,43.0,10.0,97.0,218.0,339.0,189.0
background,-68.375,-15.375,58.0,112.0,10.0,44.0,2039.0,33.0,67.0,31.0,30.0,6.0,101.0,181.0,251.0,133.0
background,-68.525,4.775,72.0,95.0,10.0,0.0,65.0,72.0,16.0,65.0,69.0,133.0,218.0,271.0,346.0,289.0

Мы можем запустить Maxent с “bradypus_swd.csv” в качестве файла образцов и “background.csv” в качестве файла слоёв предикторов (оба файла находятся в папке “swd”). Попробуйте запустить процесс - вы увидете, что он идет гораздо быстрее, потому что не нужно загружать массивы предикторов целиком. Еще одно преимущество состоит в том, что вы можете связывать образцы с условиями среды за разные промежутся времени. Напримр, у вас может быть две точки встречи из одной и той же ячейки, но разделенных во времени промежутком в 100 лет, вполне вероятно, что условия в эти два момента времени сильно отличались друг от друга. Если вы не используете формат SWD, обе записи получат абсолютно одинаковые значения переменных. Недостаток этого подхода состоит в том, что вы не сможете создать карты или выходные гриды, потому что вы не используете все данные. Обойти это можно используя “проектирование”, описанное ниже.

Запуск из командной строки

Иногда необходимо создать несколько моделей, с разными параметрами или набором предиктором. Создание моделей может быть автоматизировано посредством запуска из командной строки, это исключает необходимость многократно повторяемых действий мышью в графическом интерфейсе. Параметры командной строки могут использоваться в шелл и в bat-файлах. Пример такого файла - файл “batchExample.bat” (щелкните по нему правой кнопкой мыши и выберите открыть с помощью Notepad). Он содержит следующую строку:

java -mx512m -jar maxent.jar environmentallayers=layers togglelayertype=ecoreg samplesfile=samples\bradypus.csv outputdirectory=outputs redoifexists autorun

Эта строка говорит программе где найти слои предикторов и файл с образцами и куда положить результаты, она также указывает, что переменная ecoreg является категорийной. Флаг “autorun” говорит программе немедленно начинать выполнение, не ожидая нажатия кнопки Run. Попробуйте дважды щелкнуть мышью по файлу и посмотреть что произойдет.

Большинство параметров Maxent можно настраивать из командной строки - нажмите кнопку “Help” чтобы увидеть все возможности. В одном командном файле может быть несколько запусков программы, они будут запущены друг за другом. Можно изменить значения по умолчанию параметров изменяя их в файле “maxent.bat”. Многие из параметров также могут записываться в сокращенной форме, так, запуск модели в batchExample.bat может также выглядеть вот так:

java -mx512m -jar maxent.jar –e layers –t eco –s samples\bradypus.csv –o outputs –r -a

Репликация

Опция репликации ("replicates") может быть использована для того, чтобы прогнать модель для одного и того же вида несколько раз. Наиболее распространенное применение репликации – сэмплирование и кросс-валидация. Управлять репликацией можно либо из панели Настройки (Settings), либо через параметры командной строки. По умолчанию, при репликации используется кросс-валидация, во время которой образцы разбиваются на группы равного размера, так называемые “folds”, и модель создается по каждому из них отдельно. Оставшиеся группы потом используются для оценки точности. Кросс-валидация имеет одно большое преимущество перед единичным разбиением на тренировочный-тестовый набор: она использует все данные для валидации, что хорошо для небольших наборов данных. Таким образом, если количество репликаций равно 10, то будет создано 10 html-страниц отчетов, плюс еще одна страница суммирующая всю информацию кросс-валидации. Так же, мы получаем ROC-кривые с столбцами ошибок и средние AUC по всем моделям, а также кривые отклика со столбцами ошибок в одно стандартное отклонение. Для Bradypus, кросс-валидированная ROC-кривая показывает некоторую изменчивость моделей:

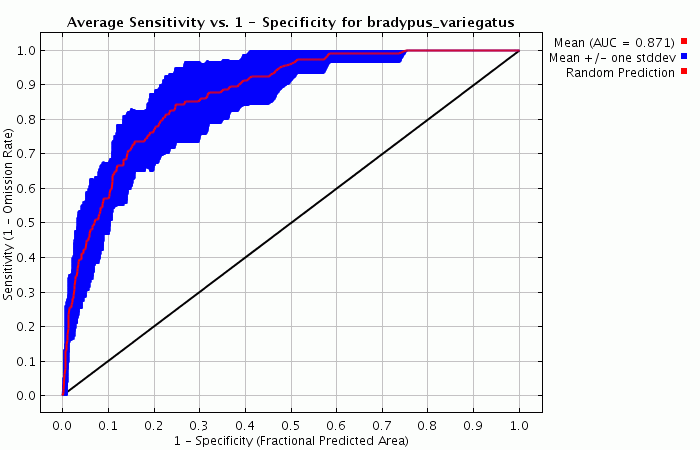
Отклик Bradypus при использовании только одной переменной годовых осадков достаточно стабилен (внизу слева), в то время как краевой отклик (marginal response) на годовые осадки меняется большее значительно (внизу справа).

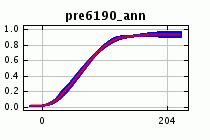
Поддерживаются две формы репликации: повторяющаяся выборка, в процессе которой образцы несколько раз случайно разбиваются на тренировочный и тестовый набор, и бутстрэппинг, когда тренировочный набор создается выборкой с заменой из образцов, количество выборок равно количеству образцов. В случае бутстрэппинга, число образцов в каждом наборе будет равно общему количеству образцов (ШТО?!), так что тренировочный набор будет содержать повторяющиеся записи.

В обоих случаях, может оказаться полезным отключение опции записи выходных матриц (“write output grids”), что не даст создавать выходные матрицы для каждой репликации и сэкономит дисковое пространство. Созданы будут только общие статистики, среднее, стандартное отклонение и т.д.

Регуляризация

Параметр “множитель регуляризации” (regularization multiplier) доступный через панель настроек управляет тем, насколько жестко выходное распределение "притягивается" к исходным данным образцов - значение меньше 1.0 (значение по умолчанию) приведет к сильнее локализованному выходному распределению, которое более точно соотвествует образцам, но это также может привести к излишнему соответствию (оверфиттинг) (подгонка к данным так тесно, что модель становится слабо генерализованной и очень плохо предсказывает независимый тестовый набор). Больший параметр регуляризации даст более широкое, менее локализованное распределение. Попробуйте изменить множитель и посмотрите на результаты и изменения в AUC. Например, установив значение множителя равным 3 мы получим такую карту, где распределение имеет более размытые границы, чем раньше:

Склонность к излишнему соответствию увеличивается с ростом сложности модели. Что бы увидеть сильно притянутую к данным модель, попробуйте сначала установить множитель равным очень небольшой величине (например 0.01) со стандартным набором объектов. Потом попробуйте тоже значение множителя с линейными и квадратичными объектами.

Предсказание

Модель, созданная на одном наборе слоёв (или файле SWD) может быть “спроецирована” путем ее применения к другому набору слоёв (или файлу SWD). Проецирование может понадобиться в ситуациях когда, например, моделируется распределение видов в меняющихся климатических условиях или для оценки инвазивного риска, когда модель нативного распределение инвазивного вида применяется для новой территории, или просто для оценки модели в наборе тестовых локаций для дальнейшего статистического анализа. Здесь мы применим проецирование для простого предсказания изменения климата, чтобы оценить трудности с которыми придется столкнуться при создании надежных моделей распределений в рамках подобных процессов.

Директория “hotlayers” содержит те же самые переменные среды, что и директория “layers” с двумя отличиями: значения переменной среднегодовой температуры (tmp6190_ann.asc) увеличены на 30, что значит равномерное (по всей поверхности) повышение температуры на 3 градуса Цельсия, в то время как значения переменной максимальных температур (tmx6190_ann.asc) увеличены на 40, т.е. повышение температуры на 4 градуса Цельсия. Эти отличия передают очень упрощенную оценку будущего климата с увеличенной средней температурой и с большой температурной изменчивостью, но без изменения в количестве осадков. Чтобы испытать модель "Bradypus" на этом новом климате, укажите программе файл выборки и современные переменные среды, используя либо грид либо формат SWD, а так же укажите путь к папке “hotlayers” в "Директории прогнозных данных" (Projection Layers Directory) как показано ниже.

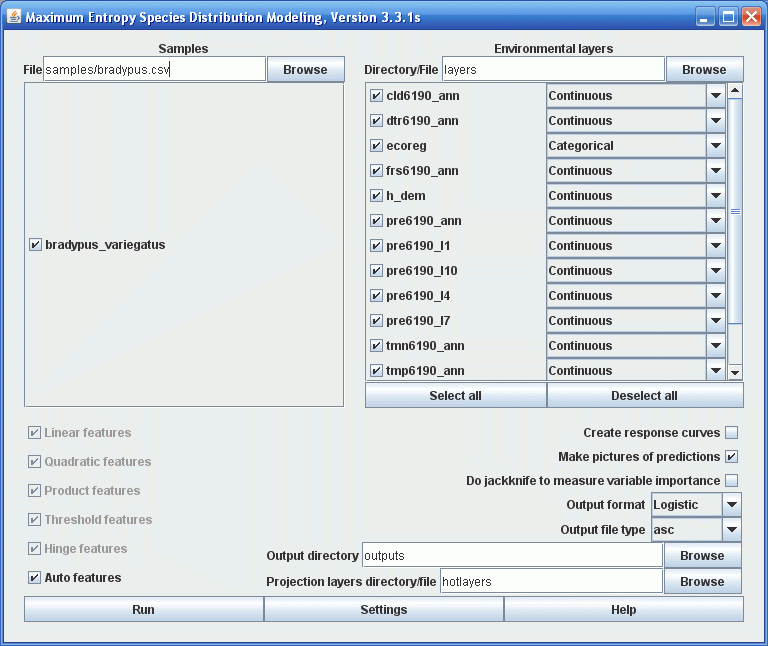
Папка с прогнозными слоями (или SWD) должна содержать переменные под теми же именами, что и переменные использованные для тренировки модели, но описывающие иные условия (например, другой географический район или иные климатические модели). И для тренировки модели и для прогнозирования, имя каждой переменной указано в заголовке табличной колонки (при использовании SWD) или имя файла без расширения .asc (если указывается директория с гридами).

После того, как вы нажмете на кнопку “Run”, модель проведет тренировку на переменных среды соответствующих современным климатическим условиям, в затем спроецирует результат на ascii-гриды из директории “hotlayers”. Результирующий ascii-грид будет назван “bradypus_variegatus_hotlayers.asc”, и как правило, имя директории добавляется к названию вида, для того, чтобы отличить его от стандартной, не прогнозной, версии. Если будет отмечено “make pictures of predictions”(создать прогнозное изображение), картинка прогнозной модели появится в “bradypus.html”. В нашем случае, был создано такое изображение:

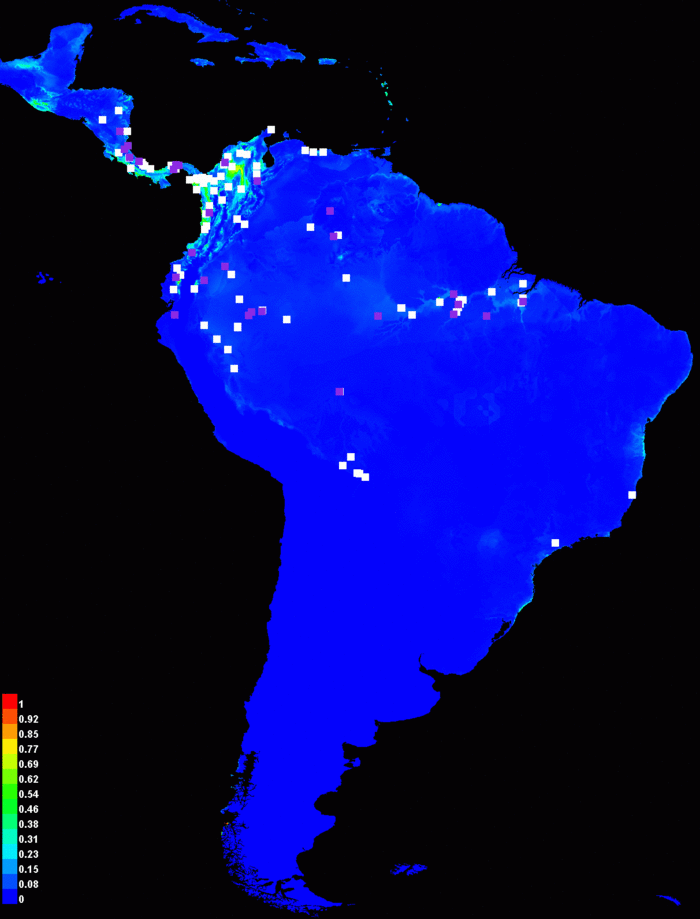
Хорошо видно, что прогнозная вероятность присутствия значительно ниже в условиях более теплого климата. Предсказание, безусловно, зависит от параметров модели, которую мы проецируем. Если мы используем только петлевые и категорийные объекты вместо отмеченных по умолчанию, прогнозное распространение гораздо существенней:

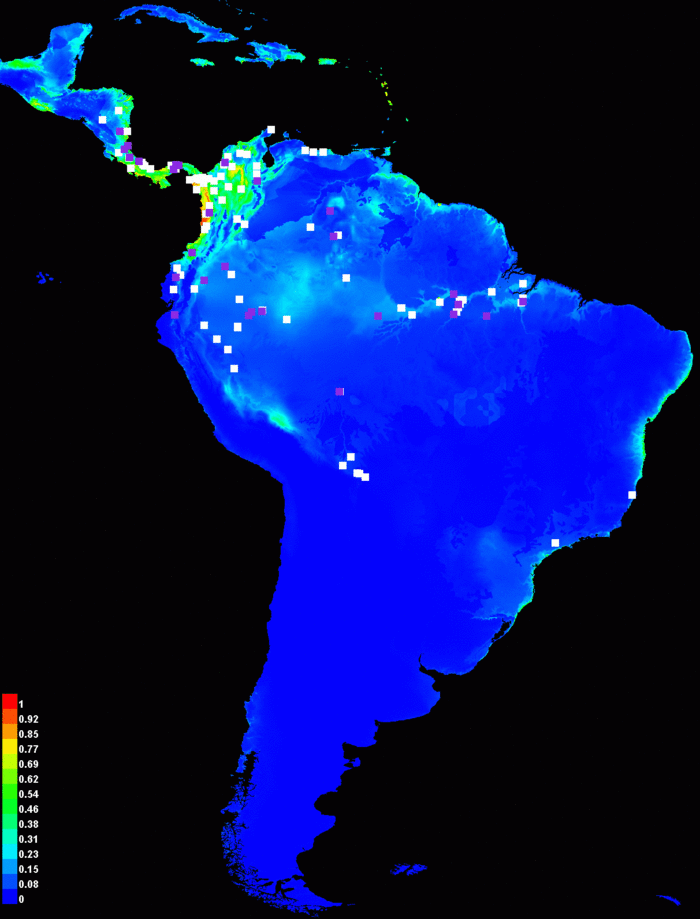
Две различные модели, которые очень похожи в области, использованной для тренировки, могут сильно отличаться, если их спроецировать в новую географическую область или в новые климатические условия. Это особенно хорошо заметно, если присутствуют скореллированные переменные, которые могут различными способами применить сходные по виду модели, поскольку корреляция между переменными может меняться в области на которую вы производите проекцию.

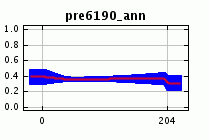
Адекватено ли полученное прогнозное уменьшение Bradypus в измененных климатических условиях? Если мы посмотрим на краевой отклик для модели с объектами по умолчанию, мы увидим, что максимум температур оказывает гораздо более сильное влияние на предсказание:

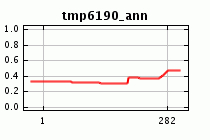
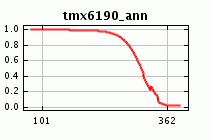
Глядя на гистограмму максимальных температур в местах известных встреч Bradypus, мы увидим, что большинство встреч (около 80%) произошло в областях с максимумами температур между 30 и 34 градусами Цельсия. Только один из них был найден в более теплой области, в то время как значительная часть предпочитала значения между 34 и 35 градусами.

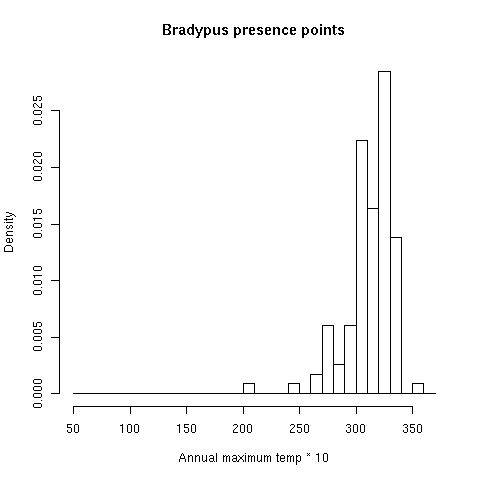
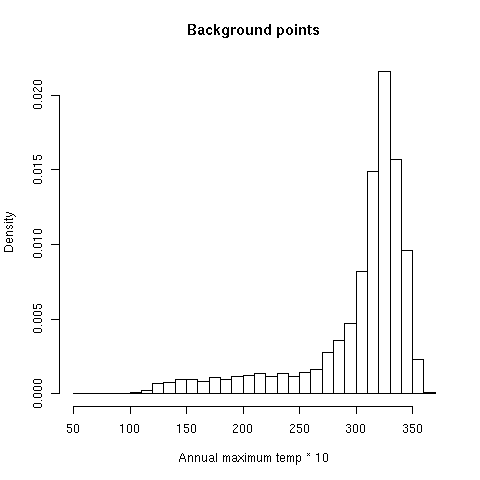
Under our climate change prediction, all 80% of the Bradypus locations currently above 30 degrees will have the maximum temperature increase to above 34 degrees. Therefore it may indeed be reasonable to predict that such locations will not be suitable for Bradypus, so Bradypus might not survive in most of its current range. Note that it is difficult to make any conclusions about why such conditions are not suitable: it may be that Bradypus is intolerant to heat, or it may be that higher maximum temperatures would allow fire to cause widespread replacement of rainforest by fire-tolerant tree species, eliminating most suitable habitat for Bradypus. To further investigate the prospects of Bradypus under climate change, we could do physiological studies to investigate the species’ tolerance for heat, or study the fire ecology of rainforest boundaries in the region.

Note: histograms like the two above are useful tools for investigating your data. They were made in R using the following commands:

swdPresence <- read.csv("swd/bradypus_swd.csv")
hist(swdPresence$tmx6190_ann, probability=TRUE, breaks=c(5:37*10), xlab="Annual maximum temp * 10", main="Bradypus presence points")
swdBackground <- read.csv("swd/background.csv")
hist(swdBackground$tmx6190_ann, probability=TRUE, breaks=c(5:37*10), xlab="Annual maximum temp * 10", main="Background points")

We can see from the histograms that Bradypus can occasionally tolerate high temperatures, as evidenced by the single record with maximum temperature of 35 degrees. On the other had, there are extremely few points in the background with temperatures of 36 or above, so we have no evidence of whether or not Bradypus can tolerate even higher temperatures, which will be widespread under the future climate prediction. This is known as the problem of novel climate conditions: when projecting, the predictor variables may take on values outside the range seen during model training. The primary way Maxent deals with this problem is “clamping”, which treats variables outside the training range as if they were at the limit of the training range. This effect can be seen in the response curves described above, as the response is held constant outside the training range. Whenever a model is projected, Maxent makes a picture that shows where clamping has had a large effect. Projecting the Bradypus model made with all features gives this clamping picture, where the values depicted are the absolute difference between predictions with and without clamping.

]

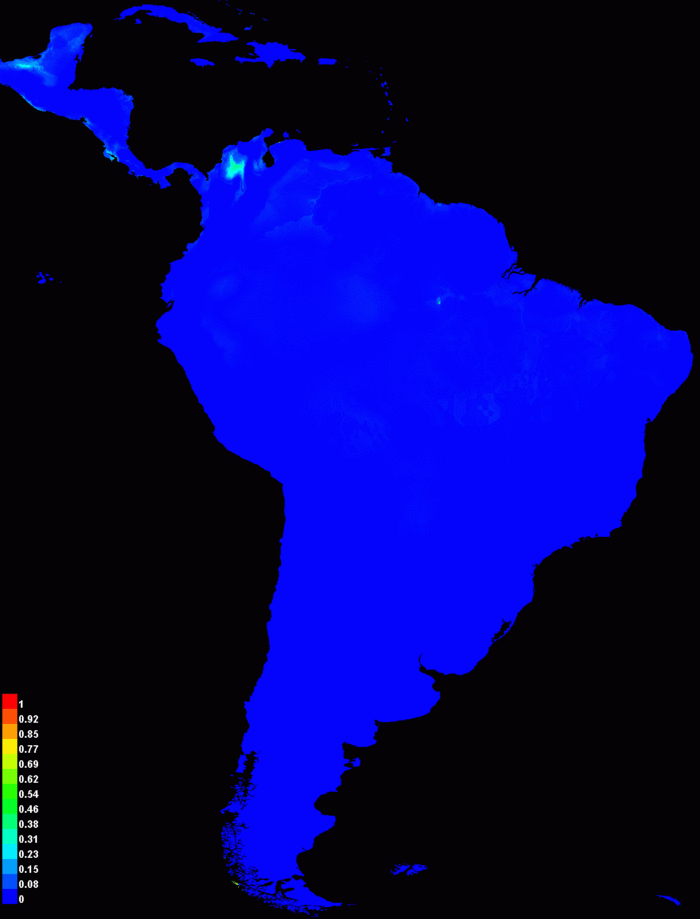Clamping has clearly had little effect in this case – in particular, the response curve for maximum temperature above shows that the prediction had already leveled off near zero at the hot end of the scale, so clamping has little effect.

We also compare the environmental variables used for projection to those used for training the model. After the clamping map, we see the following two pictures:

]]

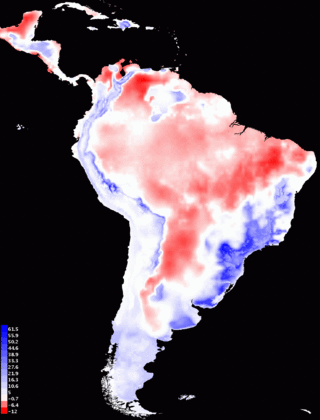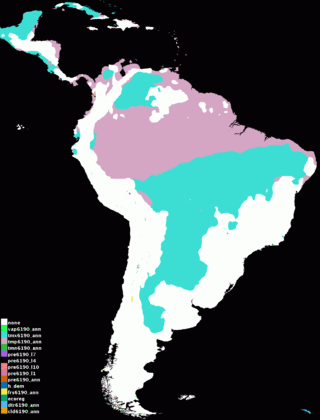The leftmost picture is a multivariate similarity surface (MESS), as described in Elith et al., Methods in Ecology and Evolution, 2010. It shows how similar each point is in hotlayers to conditions seen during model training. Negative values (shown in red) indicate novel climate, i.e., hotlayers values outside the range in layers. The value shown is the minimum over the predictors of how far out of range the point is, expressed as a fraction of the range of that predictor’s values in layers. Positive values (shown in blue) are similar to BIOCLIM values, with a score of 100 meaning that a point is not at all novel, in the sense that its hotlayers values are all exactly equal to the median value in layers. The picture on the right shows the most dissimilar variable (MoD), and as we would expect, it shows that novel climate conditions in hotlayers are due to average temperature (mauve, mostly north of the Amazon River) or maximum temperature (teal blue, mostly south of the Amazon) being outside of the training range.

Additional command-line tools

The Maxent jar file contains a number of tools that can be accessed from the command line. For Microsoft users: the features described here can be used in a batch file, like maxent.bat. As an alternative, Start->run->cmd gets you a shell for running commands interactively; cygwin (available free online) is a good alternative with a much more powerful shell that offers many unix utilities.

Quick visualization of grid file

Grid files in .asc, .grd and .mxe format, and some files in .bil format, can be viewed using the following command:

java -mx512m -cp maxent.jar density.Show filename

As with all the commands described below, you may need to add the path to the maxent.jar file and/or the file you want to view. For example, you might use:

java -mx1000m -cp C:\maxentfiles\maxent.jar density.Show C:\mydata\var1.asc

Show can take some optional arguments (immediately after density.Show):

-s sampleFile gives a file with presences to be shown in white dots

-S speciesname says which species in the sampleFile to show with dots

-r radius controls the size of the white and purple dots for occurrence records

-L removes the legend

-o writes the picture to a file in .png format

With a little Windows wizardry, you can make Show be invoked just by clicking on .asc, .grd or .mxe files. Make a batch file, say called showFile.bat, with the following single line in it:

java -mx512m -cp "c:\maxentfiles\maxent.jar" density.Show %1

then associate files of type .asc, .grd or .mxe with the batch file: from a windows explorer (a.k.a. "My Computer"), Tools->Folder Options->File Types... You may need to make the batch file executable: right click on it and follow directions.

Making an SWD file

To make an SWD-format file from a non-SWD file:

java -cp maxent.jar density.Getval samplesfile grid1 grid2 ...

where samplesfile is .csv file of occurrence data and grid1, grid2, etc. are grids in .asc, .mxe, .grd or .bil format. The output is written to "standard output", which means it appears in the command window. To write the output to a file, use a "redirect":

java -cp maxent.jar density.Getval samplesfile grid1 grid2 ... > outfile

If all the grids are in a directory you can avoid having to list them all by name by using a "wildcard":

java -cp maxent.jar density.Getval samplesfile directory/*.asc ... > outfile

because the wildcard (*) gets expanded to a list of all files that match.

Making an SWD background file

To pick a collection of background points uniformly at random from your study area:

java -cp maxent.jar density.tools.RandomSample num grid1 grid2 ...

where "num" is the number of background points desired.

Calculating AUC

The following command:

java -cp maxent.jar density.AUC testpointfile predictionfile

will calculate a presence-background AUC, where the presence points are given in the testpointfile and background points are drawn randomly from the predictionfile. The testpointfile is a .csv file (which may optionally be swd format), while the predictionfile is a grid file, typically representing the output of a species distribution model.

Projection

This tool allows you to apply a previously-calculated Maxent model to a new set of environmental data:

java -cp maxent.jar density.Project lambdaFile gridDir outFile [args]

Here lambdaFile is a .lambdas file describing a Maxent model, and gridDir is a directory containing grids for all the predictor variables described in the .lambdas file. As an alternative, gridDir could be an swd format file. The optional args can contain any flags understood by Maxent -- for example, a "grd" flag would make the output grid of density.Project be in .grd format.

File conversion

To convert a directory full of grids in one format to another:

java -cp maxent.jar density.Convert indir insuffix outdir outsuffix

where indir and outdir are directories and insuffix and outsuffix are one of asc, mxe, grd or bil.

Analyzing Maxent output in R

Maxent produces a number of output files for each run. Some of these files can be imported into other programs if you want to do your own analysis of the predictions. Here we demonstrate the use of the free statistical package R on Maxent outputs: this section is intended for users who have experience with R. We will use the following two files produced by Maxent:

bradypus_variegatus_backgroundPredictions.csv

bradypus_variegatus_samplePredictions.csv

The first file is only produced when the “writebackgroundpredictions” option is turned on, either by using a command-line flag or by selecting it from Maxent’s settings panel. The second file is always produced. Make sure you have test data (for example, by setting the random test percentage to 25); we will be evaluating the Maxent outputs using the same test data Maxent used. First we start R, and install some packages (assuming this is the first time we’re using them) and then load them by typing (or pasting):

install.packages("ROCR", dependencies=TRUE)
install.packages("vcd", dependencies=TRUE)
library(ROCR)
library(vcd)
library(boot)

Throughout this section we will use blue text to show R code and commands and green to show R outputs. Next we change directory to where the Maxent outputs are, for example:

setwd("c:/maxent/tutorial/outputs")

and then read in the Maxent predictions at the presence and background points, and extract the columns we need:

presence <- read.csv("bradypus_variegatus_samplePredictions.csv")
background <- read.csv("bradypus_variegatus_backgroundPredictions.csv")
pp <- presence$Logistic.prediction </nowiki># get the column of predictions
testpp <- pp[presence$Test.or.train=="test"] # select only test points
trainpp <- pp[presence$Test.or.train=="train"] <nowiki># select only test points
bb <- background$logistic

Now we can put the prediction values into the format required by ROCR, the package we will use to do some ROC analysis, and generate the ROC curve:

combined <- c(testpp, bb) </nowiki># combine into a single vector
label <- c(rep(1,length(testpp)),rep(0,length(bb))) # labels: 1=present, 0=random
pred <- prediction(combined, label) <nowiki># labeled predictions
perf <- performance(pred, "tpr", "fpr") # True / false positives, for ROC curve
plot(perf, colorize=TRUE) <nowiki># Show the ROC curve
performance(pred, "auc")@y.values[[1]] # Calculate the AUC

The plot command gives the following result:

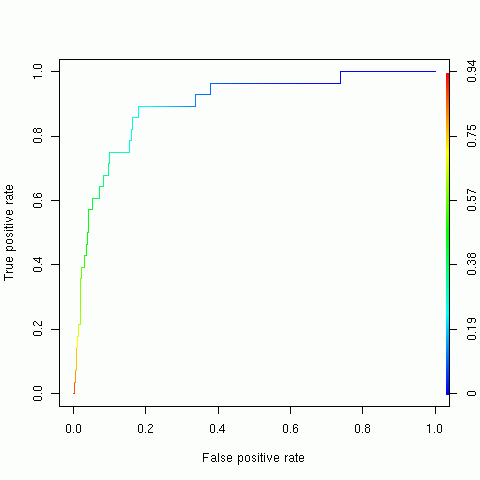
while the “performance” command gives an AUC value of 0.8677759, consistent with the AUC reported by Maxent. Next, as an example of a test available in R but not in Maxent, we will make a bootstrap estimate of the standard deviation of the AUC.

AUC <- function(p,ind) { pres <- p[ind] combined <- c(pres, bb) label <- c(rep(1,length(pres)),rep(0,length(bb))) predic <- prediction(combined, label) return(performance(predic, "auc")@y.values1) }

b1 <- boot(testpp, AUC, 100) # do 100 bootstrap AUC calculations

This gives the following output:

ORDINARY NONPARAMETRIC BOOTSTRAP

Call:
boot(data = testpp, statistic = AUC, R = 100)

Bootstrap Statistics :

original bias std. error
t1* 0.8677759 -0.0003724138 0.02972513

and we see that the bootstrap estimate of standard error (0.02972513) is close to the standard error computed by Maxent (0.028). The bootstrap results can also be used to determine confidence intervals for the AUC:

boot.ci(b1)

gives the following four estimates – see the resources section at the end of this tutorial for references that define and compare these estimates.

Intervals : 
Level Normal Basic 
95% ( 0.8099, 0.9264 ) ( 0.8104, 0.9291 ) 

Level Percentile BCa 
95% ( 0.8064, 0.9252 ) ( 0.7786, 0.9191 ) 

Those familiar with use of the bootstrap will notice that we are bootstrapping only the presence values here. We could also bootstrap the background values, but the results would not change much, given the very large number of background values (10000).

As a final example, we will investigate the calculation of binomial and Cohen’s Kappa statistics for some example threshold rules. First, the following R code calculates Kappa for the threshold given by the minimum presence prediction:

confusion <- function(thresh) {

   return(cbind(c(length(testpp[testpp>=thresh]), length(testpp[testpp<thresh])),c(length(bb[bb>=thresh]), length(bb[bb<thresh]))))

}

mykappa <- function(thresh) {

   return(Kappa(confusion(thresh)))

}

mykappa(min(trainpp))

which gives a value of 0.0072. If we want to use the threshold that minimizes the sum of sensitivity and specificity on the test data, we can do the following, using the true positive rate and false positive rate values from the “performance” object used above to plot the ROC curve:

fpr = perf@x.values[[1]]
tpr = perf@y.values[[1]]
sum = tpr + (1-fpr)
index = which.max(sum)
cutoff = perf@alpha.values[[1]][[index]]
mykappa(cutoff)

This gives a kappa value of 0.0144. To determine binomial probabilities for these two threshold values, we can do:

mybinomial <- function(thresh) { conf <- confusion(thresh) trials <- length(testpp) return(binom.test(conf11, trials, conf1,2 / length(bb), "greater")) }

mybinomial(min(trainpp))

mybinomial(cutoff)

This gives p-values of 5.979e-09 and 2.397e-11 respectively, which are both slightly larger than the p-values given by Maxent. The reason for the difference is that the number of test samples is greater than 25, the threshold above which Maxent uses a normal approximation to calculate binomial p-values.

R Resources
Some good introductory material on using R can be found at:

http://spider.stat.umn.edu/R/doc/manual/R-intro.html, and other pages at the same site.

http://www.math.ilstu.edu/dhkim/Rstuff/Rtutor.html