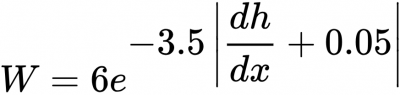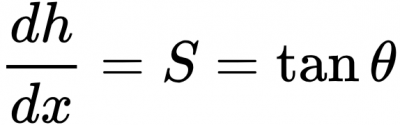Гуляем по пересеченной местности в открытых ГИС: о базовых возможностях моделирования пеших перемещений на основе QGIS, GRASS и SAGA: различия между версиями
Нет описания правки |
|||
| (не показано 28 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
{{Статья| | |||
{{Статья|Опубликована|qgis_walk_modeling}} | |||
{{Аннотация|Расчёт изохрон, оптимальных маршрутов и коридоров наименьших затрат для пеших перемещений на основе цифровых моделей рельефа в QGIS 3 (с использованием модулей GRASS и SAGA)}} | {{Аннотация|Расчёт изохрон, оптимальных маршрутов и коридоров наименьших затрат для пеших перемещений на основе цифровых моделей рельефа в QGIS 3 (с использованием модулей GRASS и SAGA)}} | ||
| Строка 18: | Строка 19: | ||
* Данные OpenStreetMap. Способы их загрузки неоднократно [http://gis-lab.info/qa/isochrone-map-grass-qgis.html#.D0.97.D0.B0.D0.B3.D1.80.D1.83.D0.B7.D0.BA.D0.B0_.D0.B4.D0.B0.D0.BD.D0.BD.D1.8B.D1.85_OSM описывались]. В статье использовалась [http://data.nextgis.com/osmshp/ архивная выгрузка с NextGIS] на Тыву. От OSM нам понадобятся границы озёр (а также, опционально, дороги, застройка, типы землепользования). | * Данные OpenStreetMap. Способы их загрузки неоднократно [http://gis-lab.info/qa/isochrone-map-grass-qgis.html#.D0.97.D0.B0.D0.B3.D1.80.D1.83.D0.B7.D0.BA.D0.B0_.D0.B4.D0.B0.D0.BD.D0.BD.D1.8B.D1.85_OSM описывались]. В статье использовалась [http://data.nextgis.com/osmshp/ архивная выгрузка с NextGIS] на Тыву. От OSM нам понадобятся границы озёр (а также, опционально, дороги, застройка, типы землепользования). | ||
* Данные о рельефе. Чем точнее ваши данные, тем лучше. В статье использовались данные с http://viewfinderpanoramas.org/dem3.html, где собраны данные на весь мир с разрешением 3 секунды. | * Данные о рельефе. Чем точнее ваши данные, тем лучше. В статье использовались данные с http://viewfinderpanoramas.org/dem3.html, где собраны данные на весь мир с разрешением 3 секунды. | ||
* Данные о типах подстилающей поверхности. В статье использовались данные [https://landcover.usgs.gov/global_climatology.php | * Данные о типах подстилающей поверхности. В статье использовались данные [https://landcover.usgs.gov/global_climatology.php MODIS Global Land Cover Climatology]. Можно обойтись и без этих данных, в статье они приводятся только в целях демонстрации принципов их учёта. | ||
Архив с данными для примера из статьи можно загрузить здесь. | Архив с данными для примера из статьи можно [https://drive.google.com/file/d/1jAjWFJJuXSk7x-AGpDejeQjlLBaanCE8/view?usp=sharing загрузить здесь]. | ||
Итак, приступаем к подготовке данных. Для начала загрузим всё необходимое в QGIS: | Итак, приступаем к подготовке данных. Для начала загрузим всё необходимое в QGIS: | ||
| Строка 98: | Строка 99: | ||
Аналогичным образом можно пометить как no-data любые другие векторные полигоны, в зависимости от ваших задач и территории. | Аналогичным образом можно пометить как no-data любые другие векторные полигоны, в зависимости от ваших задач и территории. Чтобы закончить подготовку основных данных, создадим два векторных слоя (через меню Layer - Create Layer), каждый из которых будет содержать по одной точке. Один слой назовём start_point, второй end_point - это точки, между которыми мы будем строить оптимальный маршрут и коридор наименьших затрат. Также у нас уже есть слой с точками по берегу озера - относительно них будут рассчитываться зоны доступности. | ||
[[Файл:Ogis_dem_walking_12.png|600px|thumb|center|]] | |||
== Расчёт поля стоимости перемещений == | == Расчёт поля стоимости перемещений == | ||
=== С помощью | Основная задача, лежащая в основе многих последующих расчётов, это получение поля стоимости перемещений, то есть такого растра, в каждой ячейке которого хранилась бы стоимость (например, в минутах) достижения этой ячейки из одной или множества заданных в пространстве точек. Для расчёта такого поля существует два подхода: | ||
* Интерактивный расчёт стоимостей перемещения из заданных точек. Это более сложный подход, и он востребован в тех случаях, когда невозможно назначить каждой конкретной ячейке пространства определенную стоимость её пересечения (например, если пересечение ячейки в разные стороны стоит разную цену). Одна из вариаций такого подхода доступна в модуле GRASS [https://grass.osgeo.org/grass72/manuals/r.walk.html r.walk]. | |||
* Назначение каждой ячейке базового пространства (например ЦМР) константной стоимости её пересечения, и расчёт поля стоимости от заданных точек по этим константным значениям. Это более простой подход, и его проще реализовать для произвольной функции перемещений в ГИС. В этом поможет модуль GRASS [https://grass.osgeo.org/grass72/manuals/r.cost.html r.cost]. | |||
Попробуем разобраться с обоими подходами. | |||
=== С использованием модуля r.walk === | |||
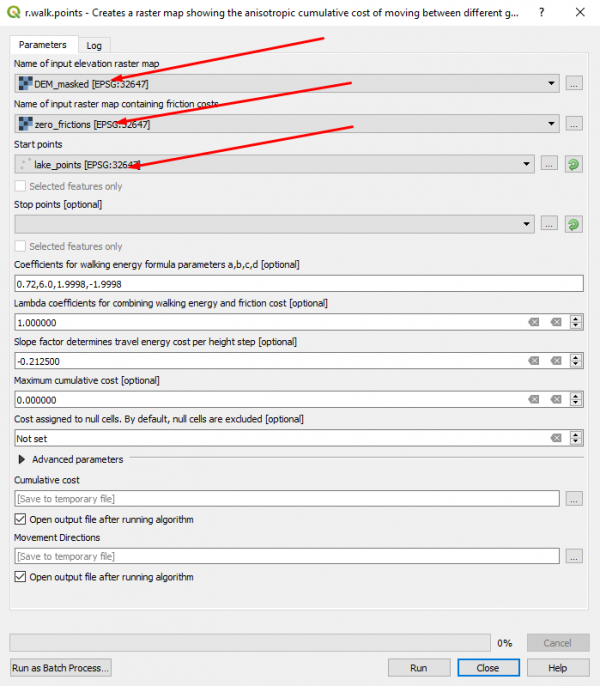
Модуль r.walk предназначен непосредственно для расчёта стоимости перемещений по пересеченной местности с учётом некоторых дополнительных условий. Остановимся на основных моментах. В QGIS запустить r.walk можно через панель анализа в GRASS - raster - r.walk.points | |||
Основные входные данные: ЦМР (elevation raster map) и слой с затратами, связанными с типом подстилающей поверхности (friction cost). | |||
С ЦМР всё ясно, она у нас уже готова. Значения в ячейках растра с friction cost будут учитываться так: это '''количество дополнительных секунд''', которые будут затрачиваться на преодоление 1 метра соответствующем пикселе. А вот такого набора данных мы ещё не подготовили! Об этом несколько позже, а пока разберёмся с другими параметрами. | |||
Start points - точки, относительно которых будет производиться расчёт стоимостей. End points - опциональный параметр, если указать какой-то слой, то расчёт стоимостей будет прекращен по достижению алгоритмом поиска точек в этом слое. | |||
Далее следуют настройки корневой формулы, по которой будет производиться расчёт. Процитируем, переведем и прокомментируем документацию: | |||
Главная формула расчёта: | |||
<pre>T = a*delta_S + b*delta_H_uphill + c*delta_H_moderate_downhill + d*delta_H_steep_downhill</pre> | |||
где: | |||
T - время движения в секундах, | |||
delta S - преодолеваемое горизонтальное расстояние в метрах (берётся из ЦМР), | |||
delta H - преодолеваемая разница высот в метрах (берётся из ЦМР), | |||
a, b, c, d - коэффициенты, связанные с движением в разных условиях. | |||
a: время в секундах, которое требуется для преодоления 1 метра на ровной поверхности. | |||
b: дополнительное время в секундах, затрачиваемое на метр перемены высоты на подъёмах. | |||
c: дополнительное время в секундах, затрачиваемое на метр перемены высоты на плавных спусках (используются положительные значения для уменьшения цены) | |||
d: дополнительное время в секундах, затрачиваемое на метр перемены высоты на крутых спусках (используются отрицательные значения для увеличения стоимости) | |||
Значения по умолчанию были предложены как стандартные для среднестатистического человека. Вы можете, изменяя их, моделировать перемещения для специальных категорий людей или для определенных видов зверей. | |||
Далее определяется коэффициент Lambda для связи полученной по формуле выше T и поверхности friction cost. Связь осуществляется по формуле: | |||
<pre>total cost = movement time cost + lambda * friction costs * delta_S</pre> | |||
где: | |||
movement time cost - время движения в секундах, рассчитанное по формуле выше, | |||
lamda - обсуждаемый коэффициент, | |||
friction costs - значение friction cost в текущем месте, | |||
delta S - преодолеваемое горизонтальное расстояние в метрах (берётся из ЦМР), | |||
Следующий параметр - slope factor. По сути, он участвует в формуле расчёта T как показатель перехода от плавного спуска (когда спуск ускоряет перемещение и приятен) к крутому спуску (когда уклон начинает работать наоборот, замедлять перемещение). Значение по умолчанию (-0.2125) соответствует тангенсу 12 градусов, т.е. угол склона меньше 12 градусов будет восприниматься как плавный, а больше 12 градусов - как крутой. | |||
Параметр Maximum cumulative cost опциональный и определяет цену, по достижению которой расчёты приостанавливаются. Например, вас интересуют только территории в пределах 2 часовой доступности, тогда следует установить этот параметр равным 7200 (в секундах). | |||
Таким образом, с помощью поверхности friction cost, коэффициентов a,b,c,d и фактора угла уклона можно достаточно гибко моделировать перемещения в рамках предлагаемой авторами модели. | |||
Оставим значения коэффициентов по умолчанию, и займемся подготовкой поверхности friction cost. Здесь всё зависит от выбранной вами модели типов подстилающей поверхности и собственных соображений о том, какой тип как влияет на скорость перемещения. Если совсем не охота об этом размышлять, можно не использовать никакой карты типов земель и просто создать в калькуляторе растров набор данных, состоящий из одних нулей. Если дать r.walk такой растр как friction cost, то на основную формулу просто не будет накладываться никаких дополнительных ограничений. Давайте попробуем вместе. В калькуляторе растров в границах слоя DEM создадим новый растр zero_frictions.tif по формуле | |||
<pre> 0 </pre> | |||
[[Файл:Ogis_dem_walking_13.png|600px|thumb|center|]] | |||
И теперь запустим r.walk с этим растром в качестве friction cost, нашей ЦМР и точками береговой линии озера в качестве Start points. Все остальные параметры оставим по умолчанию, и посмотрим, какие результаты будут получены. | |||
[[Файл:Ogis_dem_walking_14.png|600px|thumb|center|]] | |||
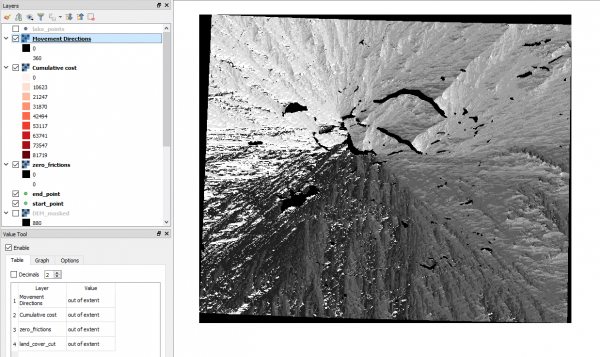
После расчётов мы получаем два новых набора данных: Cumulative cost и Movement Directions. | |||
[[Файл:Ogis_dem_walking_15.png|600px|thumb|center|]] [[Файл:Ogis_dem_walking_16.png|600px|thumb|center|]] | |||
Они оба полезны и будут использованы в дальнейших расчётах. Растр Cumulative cost в каждой ячейке содержит минимальное время перемещения от озера до этой ячейки в секундах. Растр Movement Directions содержит в каждой ячейке направление, в которые был совершен переход при расчёте Cumulative cost. По растру Cumulative cost хорошо видны неоднородности, особенно в областях с наибольшими перепадами высот. Также очевидно, что при встрече с озером (пикселями no-data) алгоритму пришлось их обходить. | |||
Теперь попробуем учесть наши типы подстилающей поверхности. Согласно [https://landcover.usgs.gov/global_climatology.php источнику] данных, в растре содержатся номера классов от 0 до 16, означающие следующее: | |||
<pre> | |||
0 Вода (Water) | |||
1 Вечнозелёные хвойные леса (Evergreen Needle leaf Forest) | |||
2 Вечнозелёные широколиственные леса (Evergreen Broadleaf Forest) | |||
3 Опадающие хвойные леса (Deciduous Needle leaf Forest) | |||
4 Опадающие широколиственные леса (Deciduous Broadleaf Forest) | |||
5 Смешанные леса (Mixed Forests) | |||
6 Плотные заросли кустарников (Closed Shrublands) | |||
7 Открытые заросли кустарников (Open Shrublands) | |||
8 Лесистные саванны (Woody Savannas) | |||
9 Саванны (Savannas) | |||
10 Поля (Grasslands) | |||
11 Постоянные болота (Permanent Wetland) | |||
12 Сельскохозяйственные поля (Croplands) | |||
13 Застройка, антропогенные сооружения (Urban and Built-Up) | |||
14 Смешанные земли с лесами, кустарниками, сельскохозяйственными полями и др. (Cropland/Natural Vegetation Mosaic) | |||
15 Снег и лёд (Snow and Ice) | |||
16 Бесплодные земли или мало покрытые растительностью (Barren or Sparsely Vegetated) | |||
</pre> | |||
Некоторые комментарии к этим классам можно найти [http://studentclimatedata.unh.edu/climate/albedo/MODISLandcoverClass_definitions.pdf здесь] (на английском языке). Понятно, что в общем случае такая классификация достаточно условна, и желательно использовать более надежные источники, непосредственно связанные с территорией исследований, а не глобальные. Для демонстрации, впрочем, вполне подойдёт. | |||
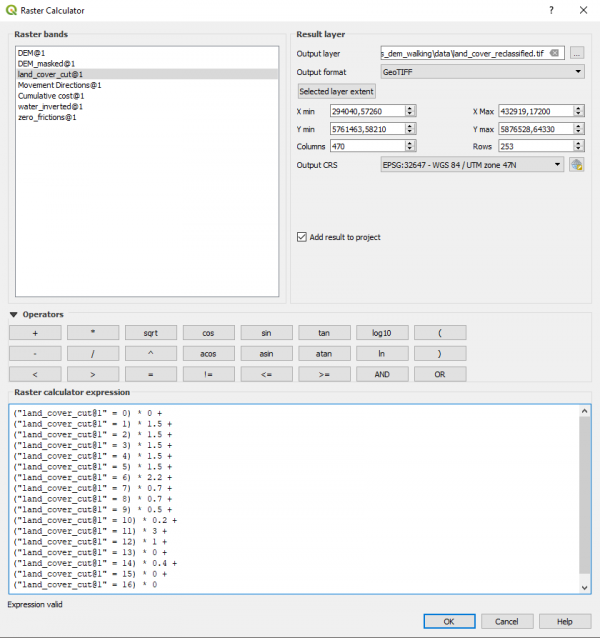
Для того, чтобы учесть эти типы земель в модели r.walk, нужно из растра с ключами создать растр со "штрафами" в секундах на метр (как следует из природы friction cost), соответствующими типам. Для такой задачи воспользуемся старым добрым способом с калькулятором растров (модули типа [https://grass.osgeo.org/grass72/manuals/r.reclass.html r.reclass] не подходят, так как работают только с целыми числами). Запишем выражение: | |||
<pre> | |||
("land_cover_cut@1" = 0) * 0 + | |||
("land_cover_cut@1" = 1) * 1.5 + | |||
("land_cover_cut@1" = 2) * 1.5 + | |||
("land_cover_cut@1" = 3) * 1.5 + | |||
("land_cover_cut@1" = 4) * 1.5 + | |||
("land_cover_cut@1" = 5) * 1.5 + | |||
("land_cover_cut@1" = 6) * 2.2 + | |||
("land_cover_cut@1" = 7) * 0.7 + | |||
("land_cover_cut@1" = 8) * 0.7 + | |||
("land_cover_cut@1" = 9) * 0.5 + | |||
("land_cover_cut@1" = 10) * 0.2 + | |||
("land_cover_cut@1" = 11) * 3 + | |||
("land_cover_cut@1" = 12) * 1 + | |||
("land_cover_cut@1" = 13) * 0 + | |||
("land_cover_cut@1" = 14) * 0.4 + | |||
("land_cover_cut@1" = 15) * 0 + | |||
("land_cover_cut@1" = 16) * 0 | |||
</pre> | |||
Логика такого выражения проста: из всех слагаемых общей суммы только одно окажется не нулевым, в нём выражение вида ("land_cover_cut@1" = N) вернёт единицу, и умножением на коэффициент мы превратим пиксель в желаемое число дополнительных секунд на метр перемещения. Коэффициенты в данном случае выбирались в целом умозрительно (на уровне "по болоту идти тяжелее всего", а заведомо отсутствующие или уже учтённые (вода) на территории классы помечены как 0), не следует использовать их как авторитетные. Подбирайте их с умом и исходя из условий своей задачи (кто перемещается и как). | |||
Результат сохраняем в land_cover_reclassified.tif | |||
[[Файл:Ogis_dem_walking_18.png|600px|thumb|center|]] | |||
В результате, если покрасить результат по красному градиенту, выходит такая картина (насыщеннее цвет - тяжелее идти): | |||
[[Файл:Ogis_dem_walking_19.png|600px|thumb|center|]] | |||
Если запустить r.walk с новой friction cost поверхностью, результат окажется совершенно иным (оставляем все настройки без изменения, только вместо zero_frictions выбираем land_cover_reclassified). Обратите внимание на то, что максимальное время увеличилось более чем в два раза. | |||
[[Файл:Ogis_dem_walking_21.png|600px|thumb|center|]] | |||
Инструмент r.walk очень мощное, классическое средство для моделирования перемещений по пересеченной местности. Однако правильный подбор коэффициентов и настройка поверхности friction cost - зачастую тема для отдельного исследования. | |||
=== С использованием альтернативных функций перемещения и r.cost === | |||
Существуют и альтернативные функции для расчёта перемещений по пересеченной местности. Одной из популярных является функция Тоблера для походов (Tobler's hiking function). Она связывает уклон поверхности и скорость перемещения по ней следующей формулой: | |||
[[Файл:Ogis_dem_walking_22.png|400px|thumb|center|]] | |||
Где | |||
[[Файл:Ogis_dem_walking_23.png|400px|thumb|center|]] | |||
И приняты обозначения: | |||
<pre> | |||
W - скорость движения (км/ч), | |||
dh - разница высот, | |||
dx - расстояние, | |||
S - уклон, | |||
θ - угол уклона. | |||
</pre> | |||
Построим график этой функции, выделив вертикальной линией угол уклона в 0 градусов: | |||
[[Файл:Ogis_dem_walking_24.png|600px|thumb|center|]] | |||
Логика функции ясна. Она ассиметрична относительно плоскости и наибольшая скорость достигается при уклоне вниз на примерно 2.86 градуса. Функция достаточно популярная, можно найти [https://gis.e-education.psu.edu/sites/default/files/capstone/Irtenkauf_596B_20140430.docx научные публикации], связанные с оценкой её точности по эмпирическим данным. | |||
Однако её ассиметричность для моделирования в ГИС крайне неудобна, если учесть, каким именно образом мы считаем углы уклона по DEM (у каждого пикселя мы определяем интегральный угол уклона, при использовании данной функции же важно, в какую именно сторону мы движемся по этому склону). Для полноценной реализации необходима интерактивная функция, как r.walk. Тем не менее мы можем, совершив некоторые допущения, рассчитать необходимое и по статическим характеристикам. Давайте предположим, что в задаче нашего моделирования каждый пиксель DEM используется для навигации во все стороны, и вниз, и вверх (что справедливо, если мы рассчитываем стоимость передвижения не только от начальной точки, но и обратно к ней). Тогда на каждом значении уклона можно просто осреднять значения функции Тоблера для положительного и отрицательного значений этого уклона. Например, если по DEM в пикселе был расчитан угол уклона равный 11 градусов, искомой скоростью перемещения будет среднее из значений функции Тоблера для уклонов в 11 и -11 градусов. Посмотрим, как функция поведёт себя в таком случае: | |||
[[Файл:Ogis_dem_walking_25.png|600px|thumb|center|]] | |||
Возьмём такую "осредненную" функцию за основу и построим модель перемещений согласно ей. Для этого возвращаемся в QGIS, и для начала расчитаем уклоны по маскированной ЦМР (DEM_masked). Для этого воспользуемся функцией Raster Terrain Analysis - Slope из панели анализа. | |||
[[Файл:Ogis_dem_walking_26.png|600px|thumb|center|]] | |||
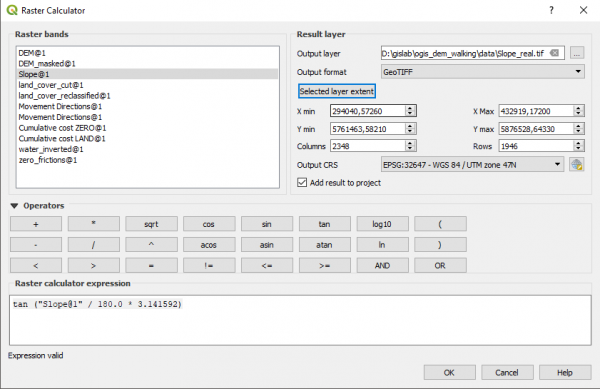
Полученный слой в каждой ячейке содержит угол уклона в градусах. С помощью калькулятора растров рассчитаем тангенсы эти углов, предварительно преобразовав их в радианы. Результирующий слой назовём Slope_real.tif | |||
<pre> | |||
tan ("Slope@1" / 180.0 * 3.141592) | |||
</pre> | |||
[[Файл:Ogis_dem_walking_27.png|600px|thumb|center|]] | |||
Посмотрим на результат: | |||
[[Файл:Ogis_dem_walking_28.png|600px|thumb|center|]] | |||
К такому слою уже можно применять усредненную функцию Тоблера. Отдельно рассчитывать тангенсы отрицательных уклонов не нужно благодаря свойству tan(-A) = -tan(A). Запишем наконец в калькуляторе растров полное выражение! | |||
<pre> | |||
(6*(2.718281^(-3.5*abs("Slope_real@1"+0.05))) + 6*(2.718281^(-3.5*abs(-1.0*"Slope_real@1"+0.05)))) / 2.0 | |||
</pre> | |||
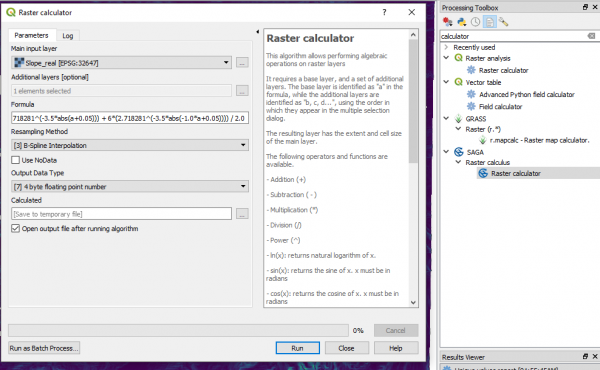
Здесь было замечено, что растровый калькулятор QGIS иногда генерирует странные значения на таких сложных выражениях, проверьте ваш результат, в нём не должно быть ячеек со значениями больше 5.5. Если они есть, то калькулятор дал сбой, но это не беда, всегда можно воспользоваться калькулятором растров SAGA, который доступен в панели анализа как SAGA - Raster calculus - Raster calculator. Там выражение несколько изменится, вместо Slope_real@1 запишем a, предварительно выбрав его в списке как основной растр для расчётов. | |||
<pre> | |||
(6*(2.718281^(-3.5*abs(a+0.05))) + 6*(2.718281^(-3.5*abs(-1.0*a+0.05)))) / 2.0 | |||
</pre> | |||
[[Файл:Ogis_dem_walking_30.png|600px|thumb|center|]] | |||
Примечание: Некоторые версии SAGA отказываются выполнять расчёт, если ничего не выбрано в меню Additional layers. Если вы получаете ошибку keyerror "XGRIDS", просто выберите в это поле любой слой, в формуле же ссылаться на него совершенно не обязательно. | |||
Результат сохраним как Tobler_speed.tif, так как в результирующем растре каждая ячейка будет хранить усредненную скорость перемещения по ней. Выглядит он так. В данном случае, чем насыщеннее цвет, тем быстрее скорость перемещения. | |||
[[Файл:Ogis_dem_walking_31.png|600px|thumb|center|]] | |||
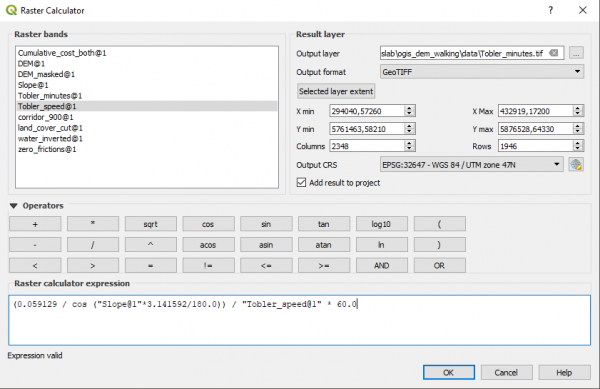
Теперь пересчитаем скорость перемещения во время с учётом пространственного разрешения. Пространственное разрешение смотрим в свойствах слоя, оно равно 59.129х59.129 метров. Для пересчёта в минуты воспользуемся простой формулой (вместо 0.059129 подставляете пространственное разрешение своего набора данных в километрах), в которой учтём увеличение преодолеваемого расстояния с увеличением уклона (для этого поделим разрешение на косинус уклона), и переведем часы в минуты: | |||
<pre> | |||
(0.059129 / cos ("Slope@1"*3.141592/180.0)) / "Tobler_speed@1" * 60.0 | |||
</pre> | |||
Результат сохраняем как Tobler_minutes - теперь каждая ячейка содержит время в минутах, которое требуется для её преодоления. | |||
[[Файл:Ogis_dem_walking_32.png|600px|thumb|center|]] | |||
На этом этапе можно добавить коэффициенты, в зависимости от задач, которые вы решаете. Если вы хотите просто изменять скорость перемещений, в калькуляторе растров достаточно умножать растр скоростей или минут на нужный коэффициент. Если необходимо учесть типы ландшафтов, вы готовите растр с коэффициентами замедления путём реклассификации карты типов земель, как это было в случае с r.walk, и умножаете растр скоростей или минут на него. Поскольку ничего нового в этой процедуре уже нет, её осуществление оставим на самостоятельную работу. Помните также о том, что у нас в наличии есть слой с уклонами, который также можно использовать в формулах с коэффициентами. | |||
=== С | Основная задача - в конце концов получить растр, содержащий в каждой ячейке затраты на её преодоление в минутах. В базовом виде это набор данных Tobler_minutes, который мы только что рассчитали. | ||
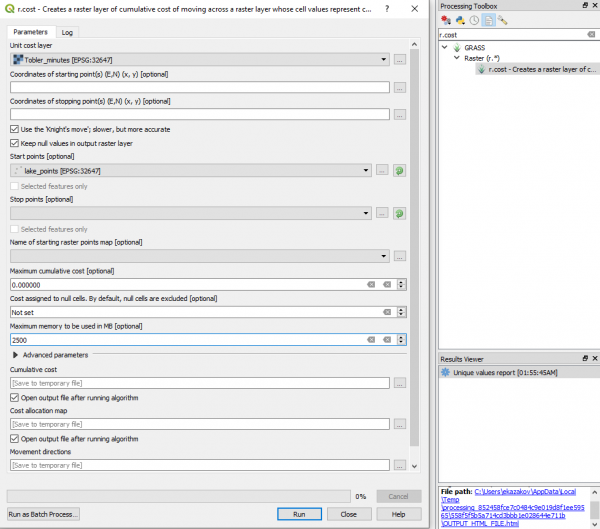
Последний шаг - расчёт собственно ценовой поверхности перемещений относительно нашего озера. В этом поможет модуль [https://grass.osgeo.org/grass72/manuals/r.cost.html r.cost], доступный в GRASS - Raster - r.cost в панели анализа. Он устроен гораздо проще, чем r.walk, но требует на вход поверхность со стоимостями преодоления каждой ячейки (которая у нас уже есть). В качестве Unit cost layer выбираем Tobler_minutes, из многообразия способов задать начальные точки выбираем слой lake_points в поле Start points, также активируем флаг "Use the Knight's move" - он позволит получить более точные результаты. Запускаем! | |||
[[Файл:Ogis_dem_walking_33.png|600px|thumb|center|]] | |||
В результате получаем уже знакомые наборы данных - Cumulative cost относительно исходных точек, и Movement Directions. Но теперь мы использовали собственную функцию! | |||
Отметим ещё раз, что при использовании r.walk вы получите '''время в секундах''', а при использовании второго подхода с r.cost - в тех единицах, к которым приведёте скорости сами. | |||
== Построение изохрон == | |||
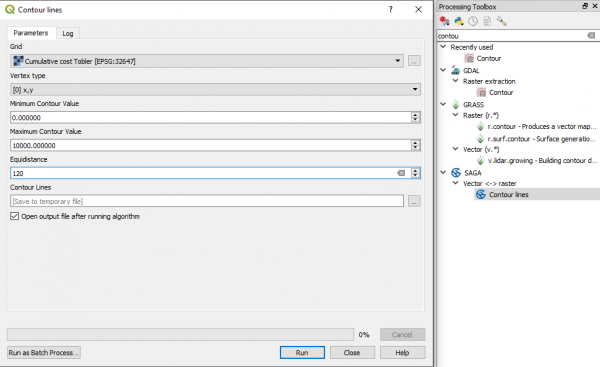
При наличии растра Cumulative cost построение изохрон - тривиальная задача. Для этого можно воспользоваться любым штатным инструментом построения изолиний по поверхностям, например SAGA - Vector <-> Raster - Contour lines в панели анализа. Зададим расстояние между изолиниями в 120 минут, и построим их для поверхности Cumulative cost, полученной по функции Тоблера. С тем же успехом мы могли использовать результат, полученный в r.walk. | |||
[[Файл:Ogis_dem_walking_34.png|600px|thumb|center|]] | |||
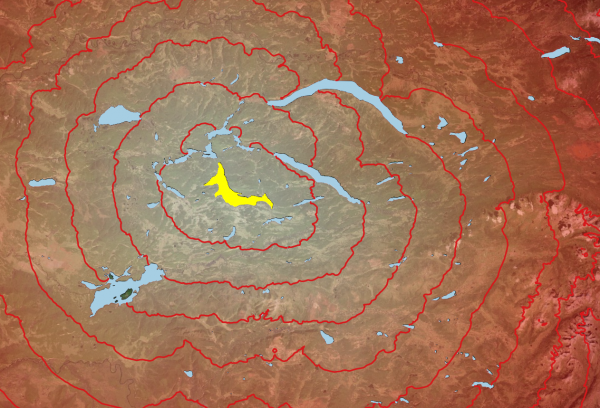
Настроив отображение, получаем такую картину (участвуют слои Bing Satellite, озёра, Cumulative cost по Тоблеру и изолинии по нему же). | |||
[[Файл:Ogis_dem_walking_35.png|600px|thumb|center|]] | |||
== Построение оптимального маршрута == | == Построение оптимального маршрута == | ||
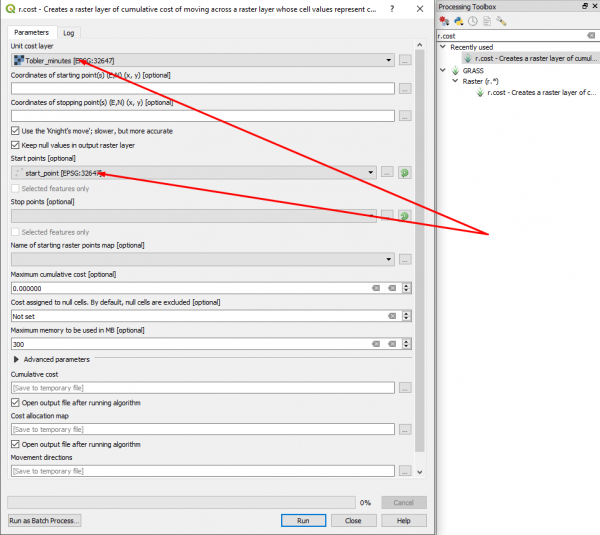
Для построения оптимального маршрута из точки в точку понадобится дополнительный модуль r.drain, доступный в GRASS - Raster - [https://grass.osgeo.org/grass72/manuals/r.drain.html r.drain] в панели анализа. Для начала необходимо с использованием любого из описанных выше подходов (r.walk или r.cost) построить Cumulative cost поверхность для одной из точек. Используем для этого слой start_points и функцию Тоблера. Благо, у нас уже есть готовая ценовая поверхность Tobler_minutes, и остаётся лишь посчитать r.cost по ней из слоя start_points. | |||
[[Файл:Ogis_dem_walking_36.png|600px|thumb|center|]] | |||
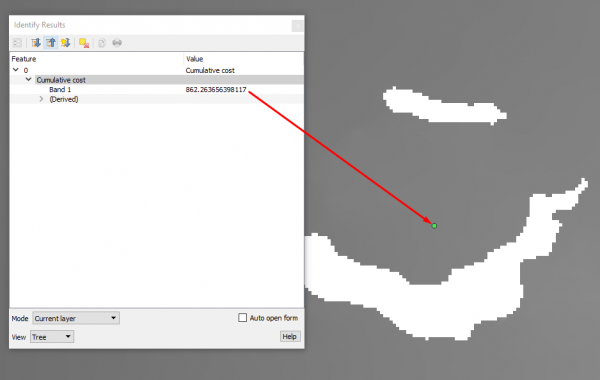
По полученной поверхности Cumulative cost можно сразу посмотреть время, которое потребуется, чтобы добраться до точки в end_point - просто используем инструмент идентификации при активном слое Cumulative cost в расположении конечной точки. 862 минуты! | |||
[[Файл:Ogis_dem_walking_37.png|600px|thumb|center|]] | |||
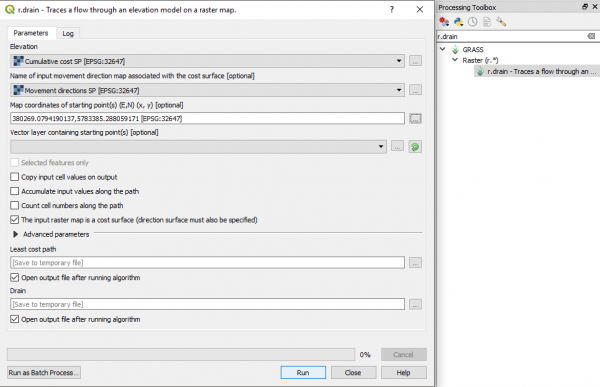
Теперь запускаем модуль r.drain. В качестве слоя Elevation выбираем полученный для начальной точки Cumulative cost, затем выбираем соответствующий ей Movement Directions (оба эти слоя были получены на предыдущем шаге), затем в vector layer containing staring points выбираем векторный слой end_point, до которого будет считаться маршрут, и обязательно ставим флаг "The input raster map is a cost surface". Часто интерфейс r.drain в QGIS немного глючит, и не запускается с выбранным векторным слоем - требует явно указать координаты точки/точек в поле Map coordinates of starting point(s). Если вы наблюдаете такое поведение, то просто с помощью кнопки справа от этого поля перейдите к интерактивному целеуказанию по карте и укажите конечную точку вручную. | |||
[[Файл:Ogis_dem_walking_38.png|600px|thumb|center|]] | |||
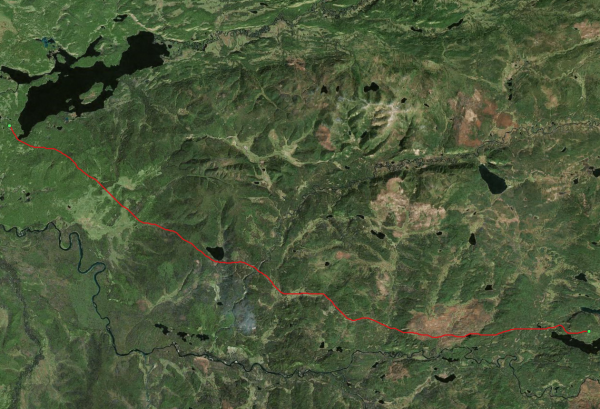
В результате будут сгенерированы два слоя: Least cost path - растр, в котором ячейками со значением 1 показаны места, по которым нужно идти (все остальные ячейки no data), и Drain - векторная линия, соответствующая этому пути. Просто нарисуем Drain поверх подложки, вот и оптимальный маршрут с учётом всех условий расчёта Cumulative cost поверхности. | |||
[[Файл:Ogis_dem_walking_39.png|600px|thumb|center|]] | |||
== Расчёт коридора наименьших затрат == | == Расчёт коридора наименьших затрат == | ||
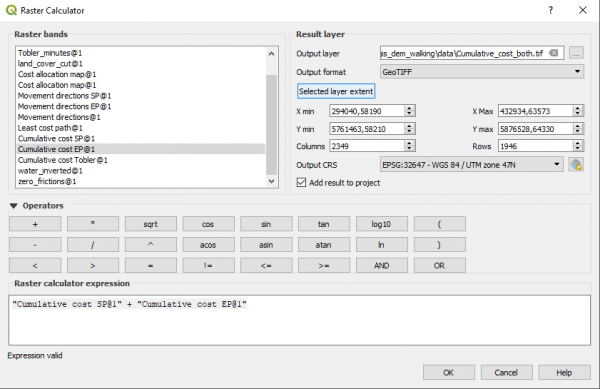
Трудно рассчитывать, что перемещение будет осуществляться чётко по оптимальной линии - скорее всего это будет некоторая совокупность оптимальных маршрутов, или, вернее сказать, область их содержащая. Она называется коридором наименьших затрат (Least cost corridor). Особенно часто такие коридоры строят те, кто изучает животных, рассчитывает области, где их можно вероятнее всего встретить, просчитывает пути миграции. На основе достигнутых нами ранее результатов построить такой коридор очень просто. Построим его между точками в start_point и end_point. Строим одним из описанных выше способов Cumulative cost поверхность для обеих точек (для start_point мы уже построили в предыдущем разделе), назовём их для различия Cumulative cost SP (start point) и Cumulative cost EP (end point). А теперь их просто складываем в калькуляторе растров: | |||
<pre> | |||
"Cumulative cost SP@1" + "Cumulative cost EP@1" | |||
</pre> | |||
Записываем результат в Cumulative_cost_both | |||
[[Файл:Ogis_dem_walking_40.png|600px|thumb|center|]] | |||
Получается вот такая объединенная поверхность. | |||
[[Файл:Ogis_dem_walking_41.png|600px|thumb|center|]] | |||
Теперь вспомним, сколько времени занимал оптимальный маршрут - порядка 860 минут. Допустим, мы готовы дать свободу в 40 дополнительных минут и посмотреть, в каких точках тогда можно будет наблюдать перемещение. То есть устанавливаем предельную цену в 900 (860+40) минут. В калькуляторе растров превратим Cumulative_cost_both в бинарный растр по порогу 900: | |||
<pre> | |||
"Cumulative_cost_both@1" >= 900 | |||
</pre> | |||
Сохраним результат в corridor_900. Получился вот такой растр, у него в области коридора значения 0, а во всех остальных 1. | |||
[[Файл:Ogis_dem_walking_42.png|600px|thumb|center|]] | |||
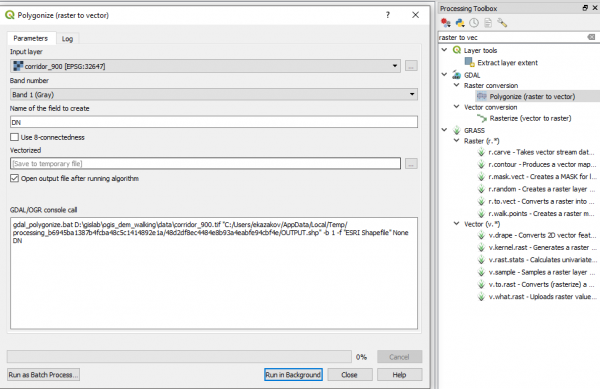
Теперь либо через стилизацию растра, либо через преобразование растра в вектор можно без труда получить карту и статистику по коридору. Давайте создадим вектор. Для это воспользуемся модулем Polygonize, который доступен в GDAL - Raster conversion - Polygonize в панели анализа | |||
[[Файл:Ogis_dem_walking_43.png|600px|thumb|center|]] | |||
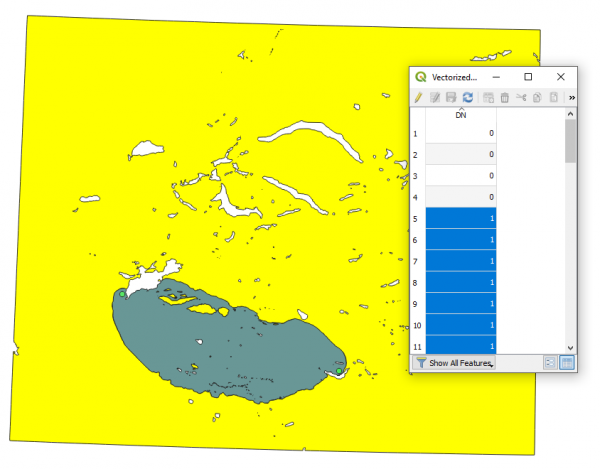
Из результирующего векторного слоя удаляем все объекты, у которых значение атрибута DN = 1 | |||
[[Файл:Ogis_dem_walking_44.png|600px|thumb|center|]] | |||
С оставшимися объектами получаем такую картину: | |||
[[Файл:Ogis_dem_walking_45.png|600px|thumb|center|]] | |||
Заодно можем оценить площадь коридора: 1182 квадратных километра. | |||
== Заключение == | |||
Благодаря модулям GRASS в открытых ГИС доступны мощные инструменты для моделирования перемещений по пересеченной местности, которые можно гибко настраивать, использовать большое количество дополнительных данных и адаптировать под свои задачи. Все наиболее популярные задачи - построение изохрон, расчёт оптимальных маршрутов и коридоров наименьших затрат успешно решаются и могут быть, при необходимости, автоматизированы. | |||
== Дополнительные сведения == | == Дополнительные сведения == | ||
| Строка 114: | Строка 488: | ||
Для QGIS 2.* существует [https://sigsemgrilhetas.wordpress.com/plugins-qgis/walking-time/ плагин Walking Time], использующий функцию Тоблера для построения маршрута. | Для QGIS 2.* существует [https://sigsemgrilhetas.wordpress.com/plugins-qgis/walking-time/ плагин Walking Time], использующий функцию Тоблера для построения маршрута. | ||
Иногда при установке QGIS 3 под Windows из панели анализа недоступны инструменты SAGA. Для того, чтобы это исправить, можно установить QGIS через OSGeo4W Installer, выбрав в разделе desktop saga-ltr вместо saga по умолчанию. | |||
Существует попытка переписать r.walk для моделирования по функции Тоблера, чтобы это работало честно в интерактивном режиме, а не с допущениями, принятыми нами. Познакомиться с кодом, чтобы попробовать собрать решение у себя на компьютере, вы можете здесь: https://github.com/fxi/AccessMod_r.walk | |||
Текущая версия от 11:39, 17 июля 2018
по адресу http://gis-lab.info/qa/qgis_walk_modeling.html
Расчёт изохрон, оптимальных маршрутов и коридоров наименьших затрат для пеших перемещений на основе цифровых моделей рельефа в QGIS 3 (с использованием модулей GRASS и SAGA)
В статье рассмотрены решения некоторых отдельных, наиболее популярных задач, связанных с моделированием пеших перемещений (людей или животных) по пересечённой местности. Потребность в такого рода моделировании часто возникает при необходимости проложить маршрут в пешем походе, определить области перемещений пределах заданных временных интервалов, а также в задачах археологии, зоологии и других дисциплин.
Рассмотрим решения для трёх базовых проблем:
- Построение изохрон перемещений по пересеченной местности относительно одной или множества исходных точек
- Построение оптимального (с точки зрения временных затрат) маршрута по пересеченной местности между двумя точками
- Построение коридора оптимальных временных затрат между двумя точками
Для подготовки данных и моделирования будем использовать открытый пакет QGIS 3.0.2 с модулями GRASS и SAGA, вызов которых доступен из панели анализа. Тестирование осуществлялось в средах Windows 10 x64 и Linux Mint 18.2 x64
Подготовка данных
Для демонстрации будет использоваться набор данных для территории Республики Тыва, в горной местности к северо-востоку от Кызыла. У озера Маны-Холь. В качестве источников использовались:
- Данные OpenStreetMap. Способы их загрузки неоднократно описывались. В статье использовалась архивная выгрузка с NextGIS на Тыву. От OSM нам понадобятся границы озёр (а также, опционально, дороги, застройка, типы землепользования).
- Данные о рельефе. Чем точнее ваши данные, тем лучше. В статье использовались данные с http://viewfinderpanoramas.org/dem3.html, где собраны данные на весь мир с разрешением 3 секунды.
- Данные о типах подстилающей поверхности. В статье использовались данные MODIS Global Land Cover Climatology. Можно обойтись и без этих данных, в статье они приводятся только в целях демонстрации принципов их учёта.
Архив с данными для примера из статьи можно загрузить здесь.
Итак, приступаем к подготовке данных. Для начала загрузим всё необходимое в QGIS:
- Векторные слои с препятствиями. Это могут быть любые объекты, по которым нельзя ходить. В нашем случае это только площадная гидрография из OSM (озёра, реки). Потенциально это может быть что угодно - здания, закрытые территории карьеров, военные полигоны и прочее.
- Загруженные данные по рельефу в .hgt
- Данные по типам подстилающей поверхности
- Спутниковая подложка Bing из плагина QuickMapServices для наглядности.
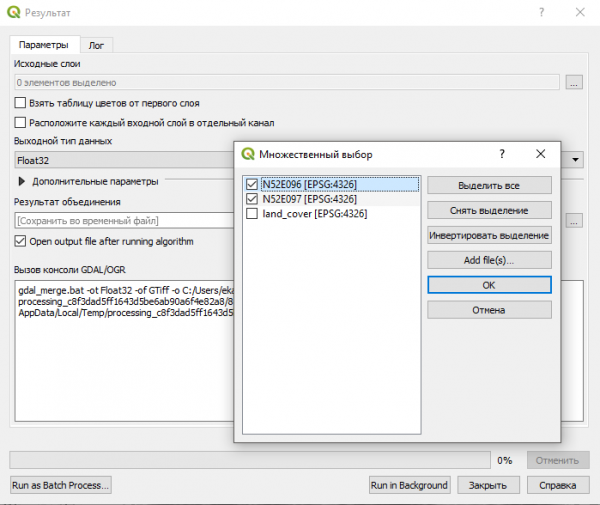
Соберём данные по рельефу в единый растровый набор. Для этого воспользуемся функцией merge из GDAL - Raster miscellaneous.
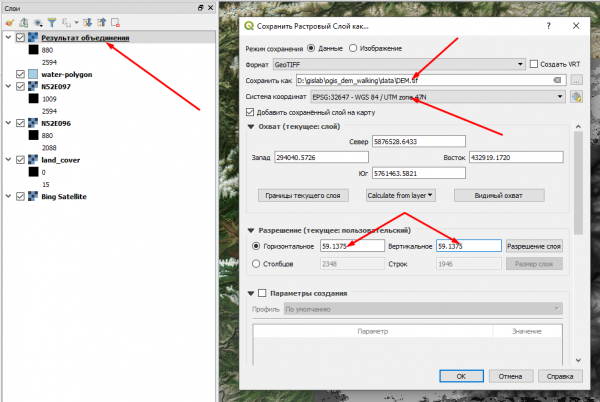
Получившийся временный слой сохраним в geotiff, с которым продолжим работу (для этого в контекстном меню слоя нужно выбрать "сохранить как". При этом в процессе сохранения произведем некоторые манипуляции. Во-первых, выберем правильную систему координат, например UTM для подходящей зоны. Для тестового участка это зона 47N (EPSG:32647). Во-вторых, для будущих задач нам потребуются данные о рельефе такие, у которых пространственное разрешение по X и Y совпадает (т.е. пиксели должны быть квадратными или почти квадратными, с пренебрежимо малой разницей). Для этого вручную устанавливаем одинаковое разрешение для обоих измерений. Проще всего приравнять большее разрешение к меньшему. Результат запишем в файл DEM.tif
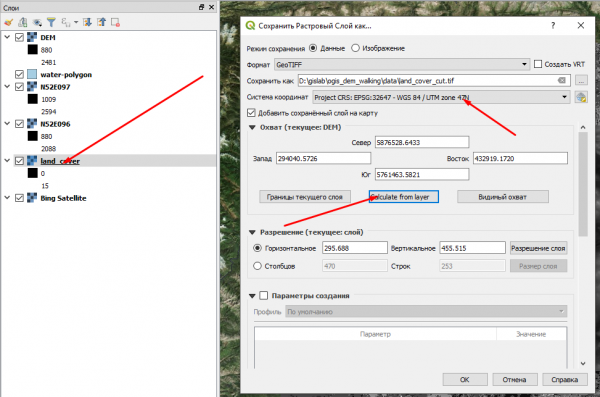
Теперь приведем к нужному виду данные о типах подстилающей поверхности. Через пункт контекстного меню "сохранить как" настраиваем нужное: устанавливаем систему координат UTM 47N и задаем новый охват равный охвату слоя с рельефом, для этого есть специальная кнопка. Всё лишнее будет отсечено. Результат сохраним в файл land_cover_cut.tif
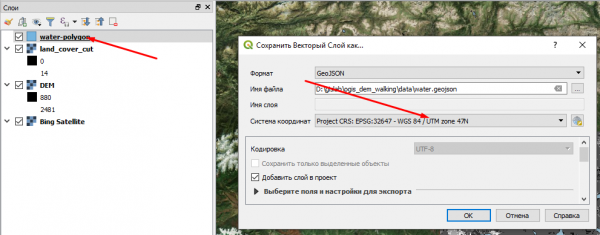
Слой с площадной гидрографией нам интересен во многих смыслах. Сохраним слой water-polygon в систему координат UTM 47N, называем water.geojson
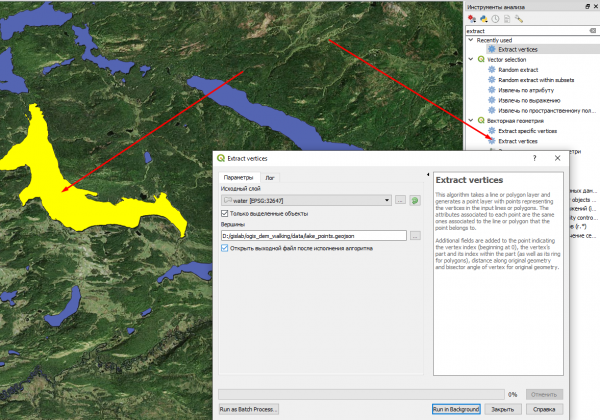
Одной из наших задач будет расчёт зон доступности озера Маны-Холь, поэтому по ходу дела получим точки его берега. Для этого выделяем в слое water это озеро, и с помощью инструмента Extract Verticies получаем слой с точками на береговой линии выделенного объекта. Сохраним его как lake-points.geojson
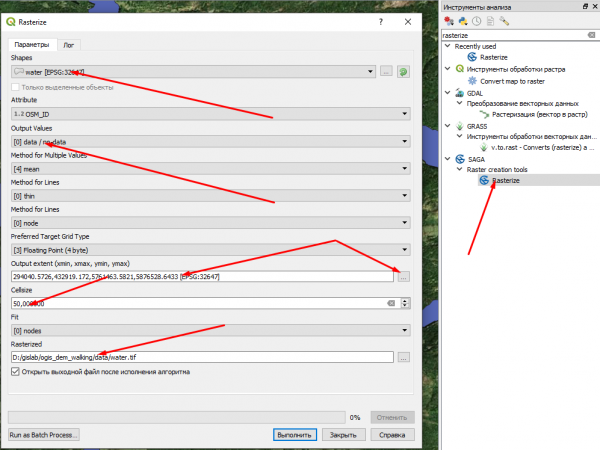
Теперь поработаем со слоями препятствий на примере той же воды. На самом деле нам нужно в слое с ЦМР (DEM.tif) установить все пиксели с препятствиями в No Data. Сделать это можно множеством способов, посмотрим на один из них. Первый шаг - растеризация векторного слоя. Используем инструмент SAGA - Raster creation tools. Задаём в качестве исходного слоя water, Output Values устанавливаем в data/no-data, указываем охват равный охвату слоя DEM (это можно сделать через контекстное меню справа от поля ввода значений), а также задаём пространственное разрешение (cellsize) равным выбранному разрешению для слоя DEM, можно выбрать значение меньше.
В результате получаем растровый слой, в котором на месте воды пиксели имеют значение 1, а во всех остальных местах - no data.
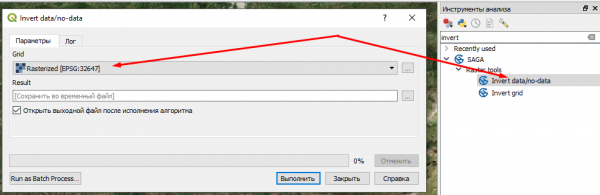
Теперь обращаем значения data / no-data с помощью простого инструмента SAGA - Raster tools - Invert data/no-data.
Теперь всё наоборот - там, где были объекты, теперь no-data. Во всех остальных местах пиксели имеют значение 1. Сохраним этот набор данных в water_inverted.tif
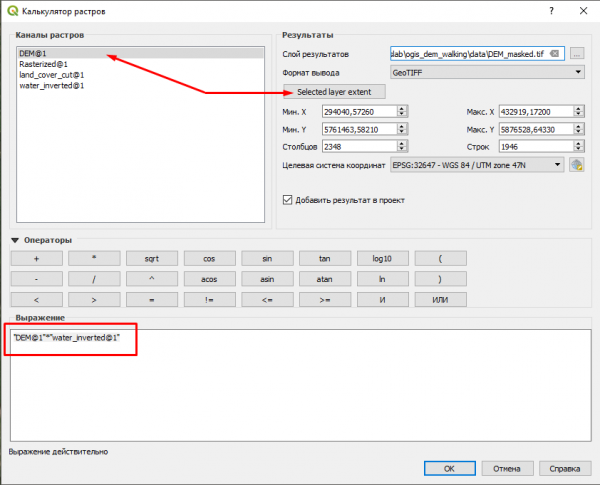
Это то, что нам нужно. Теперь можно простым способом превратить соответствующие пиксели ЦМР в no data. Для этого открываем калькулятор растров (в меню Raster), и просто перемножаем слой с ЦМР и слой water_inverted. То есть задаём такое выражение, которое расчитаем в границах DEM.tif. Результат сохраним в DEM_masked.tif.
"DEM@1"*"water_inverted@1"
Результат - желанная ЦМР с "дырками".
Аналогичным образом можно пометить как no-data любые другие векторные полигоны, в зависимости от ваших задач и территории. Чтобы закончить подготовку основных данных, создадим два векторных слоя (через меню Layer - Create Layer), каждый из которых будет содержать по одной точке. Один слой назовём start_point, второй end_point - это точки, между которыми мы будем строить оптимальный маршрут и коридор наименьших затрат. Также у нас уже есть слой с точками по берегу озера - относительно них будут рассчитываться зоны доступности.
Расчёт поля стоимости перемещений
Основная задача, лежащая в основе многих последующих расчётов, это получение поля стоимости перемещений, то есть такого растра, в каждой ячейке которого хранилась бы стоимость (например, в минутах) достижения этой ячейки из одной или множества заданных в пространстве точек. Для расчёта такого поля существует два подхода:
- Интерактивный расчёт стоимостей перемещения из заданных точек. Это более сложный подход, и он востребован в тех случаях, когда невозможно назначить каждой конкретной ячейке пространства определенную стоимость её пересечения (например, если пересечение ячейки в разные стороны стоит разную цену). Одна из вариаций такого подхода доступна в модуле GRASS r.walk.
- Назначение каждой ячейке базового пространства (например ЦМР) константной стоимости её пересечения, и расчёт поля стоимости от заданных точек по этим константным значениям. Это более простой подход, и его проще реализовать для произвольной функции перемещений в ГИС. В этом поможет модуль GRASS r.cost.
Попробуем разобраться с обоими подходами.
С использованием модуля r.walk
Модуль r.walk предназначен непосредственно для расчёта стоимости перемещений по пересеченной местности с учётом некоторых дополнительных условий. Остановимся на основных моментах. В QGIS запустить r.walk можно через панель анализа в GRASS - raster - r.walk.points
Основные входные данные: ЦМР (elevation raster map) и слой с затратами, связанными с типом подстилающей поверхности (friction cost).
С ЦМР всё ясно, она у нас уже готова. Значения в ячейках растра с friction cost будут учитываться так: это количество дополнительных секунд, которые будут затрачиваться на преодоление 1 метра соответствующем пикселе. А вот такого набора данных мы ещё не подготовили! Об этом несколько позже, а пока разберёмся с другими параметрами.
Start points - точки, относительно которых будет производиться расчёт стоимостей. End points - опциональный параметр, если указать какой-то слой, то расчёт стоимостей будет прекращен по достижению алгоритмом поиска точек в этом слое.
Далее следуют настройки корневой формулы, по которой будет производиться расчёт. Процитируем, переведем и прокомментируем документацию:
Главная формула расчёта:
T = a*delta_S + b*delta_H_uphill + c*delta_H_moderate_downhill + d*delta_H_steep_downhill
где:
T - время движения в секундах,
delta S - преодолеваемое горизонтальное расстояние в метрах (берётся из ЦМР),
delta H - преодолеваемая разница высот в метрах (берётся из ЦМР),
a, b, c, d - коэффициенты, связанные с движением в разных условиях.
a: время в секундах, которое требуется для преодоления 1 метра на ровной поверхности.
b: дополнительное время в секундах, затрачиваемое на метр перемены высоты на подъёмах.
c: дополнительное время в секундах, затрачиваемое на метр перемены высоты на плавных спусках (используются положительные значения для уменьшения цены)
d: дополнительное время в секундах, затрачиваемое на метр перемены высоты на крутых спусках (используются отрицательные значения для увеличения стоимости)
Значения по умолчанию были предложены как стандартные для среднестатистического человека. Вы можете, изменяя их, моделировать перемещения для специальных категорий людей или для определенных видов зверей.
Далее определяется коэффициент Lambda для связи полученной по формуле выше T и поверхности friction cost. Связь осуществляется по формуле:
total cost = movement time cost + lambda * friction costs * delta_S
где:
movement time cost - время движения в секундах, рассчитанное по формуле выше,
lamda - обсуждаемый коэффициент,
friction costs - значение friction cost в текущем месте,
delta S - преодолеваемое горизонтальное расстояние в метрах (берётся из ЦМР),
Следующий параметр - slope factor. По сути, он участвует в формуле расчёта T как показатель перехода от плавного спуска (когда спуск ускоряет перемещение и приятен) к крутому спуску (когда уклон начинает работать наоборот, замедлять перемещение). Значение по умолчанию (-0.2125) соответствует тангенсу 12 градусов, т.е. угол склона меньше 12 градусов будет восприниматься как плавный, а больше 12 градусов - как крутой.
Параметр Maximum cumulative cost опциональный и определяет цену, по достижению которой расчёты приостанавливаются. Например, вас интересуют только территории в пределах 2 часовой доступности, тогда следует установить этот параметр равным 7200 (в секундах).
Таким образом, с помощью поверхности friction cost, коэффициентов a,b,c,d и фактора угла уклона можно достаточно гибко моделировать перемещения в рамках предлагаемой авторами модели.
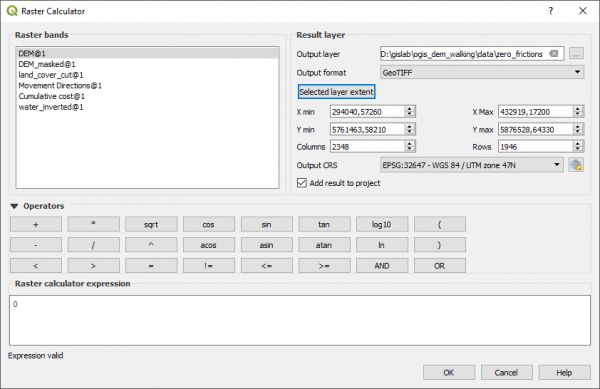
Оставим значения коэффициентов по умолчанию, и займемся подготовкой поверхности friction cost. Здесь всё зависит от выбранной вами модели типов подстилающей поверхности и собственных соображений о том, какой тип как влияет на скорость перемещения. Если совсем не охота об этом размышлять, можно не использовать никакой карты типов земель и просто создать в калькуляторе растров набор данных, состоящий из одних нулей. Если дать r.walk такой растр как friction cost, то на основную формулу просто не будет накладываться никаких дополнительных ограничений. Давайте попробуем вместе. В калькуляторе растров в границах слоя DEM создадим новый растр zero_frictions.tif по формуле
0
И теперь запустим r.walk с этим растром в качестве friction cost, нашей ЦМР и точками береговой линии озера в качестве Start points. Все остальные параметры оставим по умолчанию, и посмотрим, какие результаты будут получены.
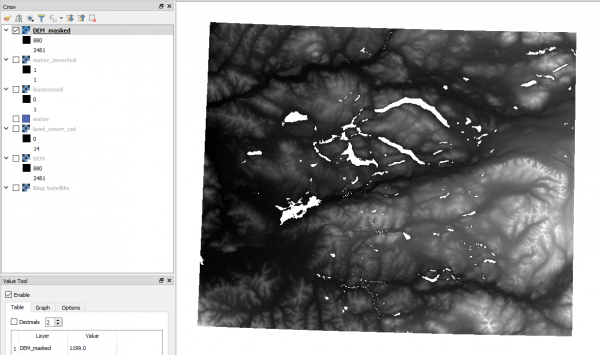
После расчётов мы получаем два новых набора данных: Cumulative cost и Movement Directions.
Они оба полезны и будут использованы в дальнейших расчётах. Растр Cumulative cost в каждой ячейке содержит минимальное время перемещения от озера до этой ячейки в секундах. Растр Movement Directions содержит в каждой ячейке направление, в которые был совершен переход при расчёте Cumulative cost. По растру Cumulative cost хорошо видны неоднородности, особенно в областях с наибольшими перепадами высот. Также очевидно, что при встрече с озером (пикселями no-data) алгоритму пришлось их обходить.
Теперь попробуем учесть наши типы подстилающей поверхности. Согласно источнику данных, в растре содержатся номера классов от 0 до 16, означающие следующее:
0 Вода (Water) 1 Вечнозелёные хвойные леса (Evergreen Needle leaf Forest) 2 Вечнозелёные широколиственные леса (Evergreen Broadleaf Forest) 3 Опадающие хвойные леса (Deciduous Needle leaf Forest) 4 Опадающие широколиственные леса (Deciduous Broadleaf Forest) 5 Смешанные леса (Mixed Forests) 6 Плотные заросли кустарников (Closed Shrublands) 7 Открытые заросли кустарников (Open Shrublands) 8 Лесистные саванны (Woody Savannas) 9 Саванны (Savannas) 10 Поля (Grasslands) 11 Постоянные болота (Permanent Wetland) 12 Сельскохозяйственные поля (Croplands) 13 Застройка, антропогенные сооружения (Urban and Built-Up) 14 Смешанные земли с лесами, кустарниками, сельскохозяйственными полями и др. (Cropland/Natural Vegetation Mosaic) 15 Снег и лёд (Snow and Ice) 16 Бесплодные земли или мало покрытые растительностью (Barren or Sparsely Vegetated)
Некоторые комментарии к этим классам можно найти здесь (на английском языке). Понятно, что в общем случае такая классификация достаточно условна, и желательно использовать более надежные источники, непосредственно связанные с территорией исследований, а не глобальные. Для демонстрации, впрочем, вполне подойдёт.
Для того, чтобы учесть эти типы земель в модели r.walk, нужно из растра с ключами создать растр со "штрафами" в секундах на метр (как следует из природы friction cost), соответствующими типам. Для такой задачи воспользуемся старым добрым способом с калькулятором растров (модули типа r.reclass не подходят, так как работают только с целыми числами). Запишем выражение:
("land_cover_cut@1" = 0) * 0 +
("land_cover_cut@1" = 1) * 1.5 +
("land_cover_cut@1" = 2) * 1.5 +
("land_cover_cut@1" = 3) * 1.5 +
("land_cover_cut@1" = 4) * 1.5 +
("land_cover_cut@1" = 5) * 1.5 +
("land_cover_cut@1" = 6) * 2.2 +
("land_cover_cut@1" = 7) * 0.7 +
("land_cover_cut@1" = 8) * 0.7 +
("land_cover_cut@1" = 9) * 0.5 +
("land_cover_cut@1" = 10) * 0.2 +
("land_cover_cut@1" = 11) * 3 +
("land_cover_cut@1" = 12) * 1 +
("land_cover_cut@1" = 13) * 0 +
("land_cover_cut@1" = 14) * 0.4 +
("land_cover_cut@1" = 15) * 0 +
("land_cover_cut@1" = 16) * 0
Логика такого выражения проста: из всех слагаемых общей суммы только одно окажется не нулевым, в нём выражение вида ("land_cover_cut@1" = N) вернёт единицу, и умножением на коэффициент мы превратим пиксель в желаемое число дополнительных секунд на метр перемещения. Коэффициенты в данном случае выбирались в целом умозрительно (на уровне "по болоту идти тяжелее всего", а заведомо отсутствующие или уже учтённые (вода) на территории классы помечены как 0), не следует использовать их как авторитетные. Подбирайте их с умом и исходя из условий своей задачи (кто перемещается и как).
Результат сохраняем в land_cover_reclassified.tif
В результате, если покрасить результат по красному градиенту, выходит такая картина (насыщеннее цвет - тяжелее идти):
Если запустить r.walk с новой friction cost поверхностью, результат окажется совершенно иным (оставляем все настройки без изменения, только вместо zero_frictions выбираем land_cover_reclassified). Обратите внимание на то, что максимальное время увеличилось более чем в два раза.
Инструмент r.walk очень мощное, классическое средство для моделирования перемещений по пересеченной местности. Однако правильный подбор коэффициентов и настройка поверхности friction cost - зачастую тема для отдельного исследования.
С использованием альтернативных функций перемещения и r.cost
Существуют и альтернативные функции для расчёта перемещений по пересеченной местности. Одной из популярных является функция Тоблера для походов (Tobler's hiking function). Она связывает уклон поверхности и скорость перемещения по ней следующей формулой:
Где
И приняты обозначения:
W - скорость движения (км/ч), dh - разница высот, dx - расстояние, S - уклон, θ - угол уклона.
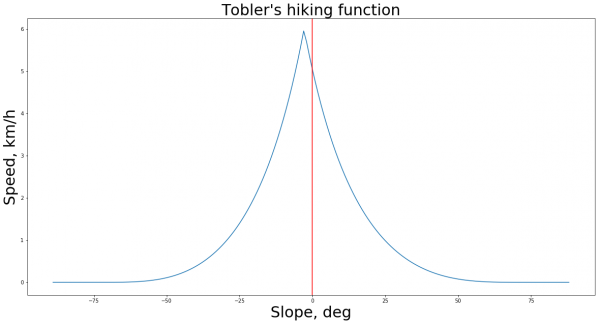
Построим график этой функции, выделив вертикальной линией угол уклона в 0 градусов:
Логика функции ясна. Она ассиметрична относительно плоскости и наибольшая скорость достигается при уклоне вниз на примерно 2.86 градуса. Функция достаточно популярная, можно найти научные публикации, связанные с оценкой её точности по эмпирическим данным.
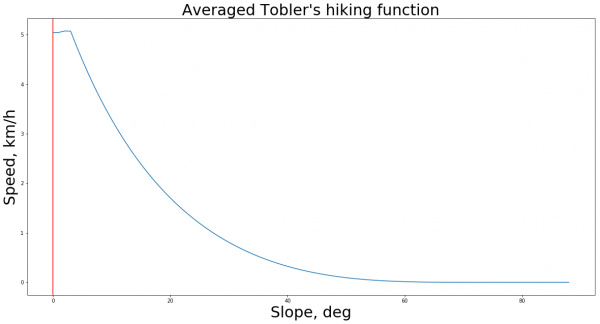
Однако её ассиметричность для моделирования в ГИС крайне неудобна, если учесть, каким именно образом мы считаем углы уклона по DEM (у каждого пикселя мы определяем интегральный угол уклона, при использовании данной функции же важно, в какую именно сторону мы движемся по этому склону). Для полноценной реализации необходима интерактивная функция, как r.walk. Тем не менее мы можем, совершив некоторые допущения, рассчитать необходимое и по статическим характеристикам. Давайте предположим, что в задаче нашего моделирования каждый пиксель DEM используется для навигации во все стороны, и вниз, и вверх (что справедливо, если мы рассчитываем стоимость передвижения не только от начальной точки, но и обратно к ней). Тогда на каждом значении уклона можно просто осреднять значения функции Тоблера для положительного и отрицательного значений этого уклона. Например, если по DEM в пикселе был расчитан угол уклона равный 11 градусов, искомой скоростью перемещения будет среднее из значений функции Тоблера для уклонов в 11 и -11 градусов. Посмотрим, как функция поведёт себя в таком случае:
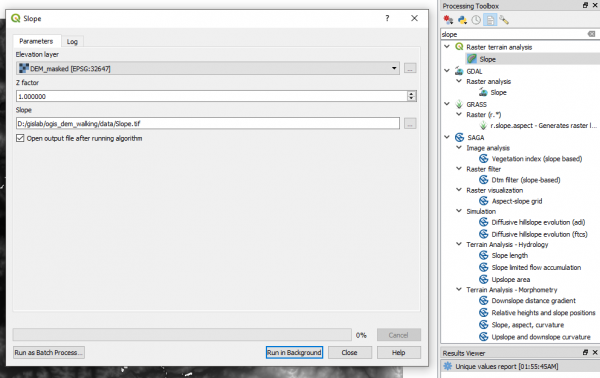
Возьмём такую "осредненную" функцию за основу и построим модель перемещений согласно ей. Для этого возвращаемся в QGIS, и для начала расчитаем уклоны по маскированной ЦМР (DEM_masked). Для этого воспользуемся функцией Raster Terrain Analysis - Slope из панели анализа.
Полученный слой в каждой ячейке содержит угол уклона в градусах. С помощью калькулятора растров рассчитаем тангенсы эти углов, предварительно преобразовав их в радианы. Результирующий слой назовём Slope_real.tif
tan ("Slope@1" / 180.0 * 3.141592)
Посмотрим на результат:
К такому слою уже можно применять усредненную функцию Тоблера. Отдельно рассчитывать тангенсы отрицательных уклонов не нужно благодаря свойству tan(-A) = -tan(A). Запишем наконец в калькуляторе растров полное выражение!
(6*(2.718281^(-3.5*abs("Slope_real@1"+0.05))) + 6*(2.718281^(-3.5*abs(-1.0*"Slope_real@1"+0.05)))) / 2.0
Здесь было замечено, что растровый калькулятор QGIS иногда генерирует странные значения на таких сложных выражениях, проверьте ваш результат, в нём не должно быть ячеек со значениями больше 5.5. Если они есть, то калькулятор дал сбой, но это не беда, всегда можно воспользоваться калькулятором растров SAGA, который доступен в панели анализа как SAGA - Raster calculus - Raster calculator. Там выражение несколько изменится, вместо Slope_real@1 запишем a, предварительно выбрав его в списке как основной растр для расчётов.
(6*(2.718281^(-3.5*abs(a+0.05))) + 6*(2.718281^(-3.5*abs(-1.0*a+0.05)))) / 2.0
Примечание: Некоторые версии SAGA отказываются выполнять расчёт, если ничего не выбрано в меню Additional layers. Если вы получаете ошибку keyerror "XGRIDS", просто выберите в это поле любой слой, в формуле же ссылаться на него совершенно не обязательно.
Результат сохраним как Tobler_speed.tif, так как в результирующем растре каждая ячейка будет хранить усредненную скорость перемещения по ней. Выглядит он так. В данном случае, чем насыщеннее цвет, тем быстрее скорость перемещения.
Теперь пересчитаем скорость перемещения во время с учётом пространственного разрешения. Пространственное разрешение смотрим в свойствах слоя, оно равно 59.129х59.129 метров. Для пересчёта в минуты воспользуемся простой формулой (вместо 0.059129 подставляете пространственное разрешение своего набора данных в километрах), в которой учтём увеличение преодолеваемого расстояния с увеличением уклона (для этого поделим разрешение на косинус уклона), и переведем часы в минуты:
(0.059129 / cos ("Slope@1"*3.141592/180.0)) / "Tobler_speed@1" * 60.0
Результат сохраняем как Tobler_minutes - теперь каждая ячейка содержит время в минутах, которое требуется для её преодоления.
На этом этапе можно добавить коэффициенты, в зависимости от задач, которые вы решаете. Если вы хотите просто изменять скорость перемещений, в калькуляторе растров достаточно умножать растр скоростей или минут на нужный коэффициент. Если необходимо учесть типы ландшафтов, вы готовите растр с коэффициентами замедления путём реклассификации карты типов земель, как это было в случае с r.walk, и умножаете растр скоростей или минут на него. Поскольку ничего нового в этой процедуре уже нет, её осуществление оставим на самостоятельную работу. Помните также о том, что у нас в наличии есть слой с уклонами, который также можно использовать в формулах с коэффициентами.
Основная задача - в конце концов получить растр, содержащий в каждой ячейке затраты на её преодоление в минутах. В базовом виде это набор данных Tobler_minutes, который мы только что рассчитали.
Последний шаг - расчёт собственно ценовой поверхности перемещений относительно нашего озера. В этом поможет модуль r.cost, доступный в GRASS - Raster - r.cost в панели анализа. Он устроен гораздо проще, чем r.walk, но требует на вход поверхность со стоимостями преодоления каждой ячейки (которая у нас уже есть). В качестве Unit cost layer выбираем Tobler_minutes, из многообразия способов задать начальные точки выбираем слой lake_points в поле Start points, также активируем флаг "Use the Knight's move" - он позволит получить более точные результаты. Запускаем!
В результате получаем уже знакомые наборы данных - Cumulative cost относительно исходных точек, и Movement Directions. Но теперь мы использовали собственную функцию!
Отметим ещё раз, что при использовании r.walk вы получите время в секундах, а при использовании второго подхода с r.cost - в тех единицах, к которым приведёте скорости сами.
Построение изохрон
При наличии растра Cumulative cost построение изохрон - тривиальная задача. Для этого можно воспользоваться любым штатным инструментом построения изолиний по поверхностям, например SAGA - Vector <-> Raster - Contour lines в панели анализа. Зададим расстояние между изолиниями в 120 минут, и построим их для поверхности Cumulative cost, полученной по функции Тоблера. С тем же успехом мы могли использовать результат, полученный в r.walk.
Настроив отображение, получаем такую картину (участвуют слои Bing Satellite, озёра, Cumulative cost по Тоблеру и изолинии по нему же).
Построение оптимального маршрута
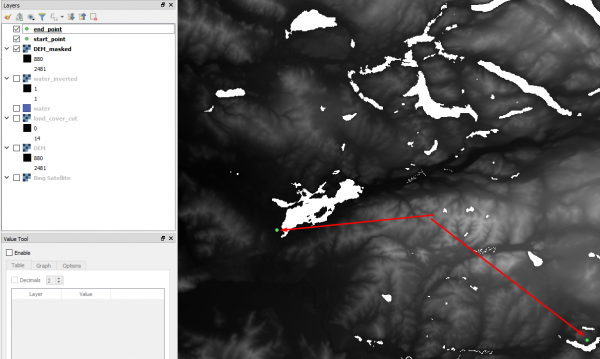
Для построения оптимального маршрута из точки в точку понадобится дополнительный модуль r.drain, доступный в GRASS - Raster - r.drain в панели анализа. Для начала необходимо с использованием любого из описанных выше подходов (r.walk или r.cost) построить Cumulative cost поверхность для одной из точек. Используем для этого слой start_points и функцию Тоблера. Благо, у нас уже есть готовая ценовая поверхность Tobler_minutes, и остаётся лишь посчитать r.cost по ней из слоя start_points.
По полученной поверхности Cumulative cost можно сразу посмотреть время, которое потребуется, чтобы добраться до точки в end_point - просто используем инструмент идентификации при активном слое Cumulative cost в расположении конечной точки. 862 минуты!
Теперь запускаем модуль r.drain. В качестве слоя Elevation выбираем полученный для начальной точки Cumulative cost, затем выбираем соответствующий ей Movement Directions (оба эти слоя были получены на предыдущем шаге), затем в vector layer containing staring points выбираем векторный слой end_point, до которого будет считаться маршрут, и обязательно ставим флаг "The input raster map is a cost surface". Часто интерфейс r.drain в QGIS немного глючит, и не запускается с выбранным векторным слоем - требует явно указать координаты точки/точек в поле Map coordinates of starting point(s). Если вы наблюдаете такое поведение, то просто с помощью кнопки справа от этого поля перейдите к интерактивному целеуказанию по карте и укажите конечную точку вручную.
В результате будут сгенерированы два слоя: Least cost path - растр, в котором ячейками со значением 1 показаны места, по которым нужно идти (все остальные ячейки no data), и Drain - векторная линия, соответствующая этому пути. Просто нарисуем Drain поверх подложки, вот и оптимальный маршрут с учётом всех условий расчёта Cumulative cost поверхности.
Расчёт коридора наименьших затрат
Трудно рассчитывать, что перемещение будет осуществляться чётко по оптимальной линии - скорее всего это будет некоторая совокупность оптимальных маршрутов, или, вернее сказать, область их содержащая. Она называется коридором наименьших затрат (Least cost corridor). Особенно часто такие коридоры строят те, кто изучает животных, рассчитывает области, где их можно вероятнее всего встретить, просчитывает пути миграции. На основе достигнутых нами ранее результатов построить такой коридор очень просто. Построим его между точками в start_point и end_point. Строим одним из описанных выше способов Cumulative cost поверхность для обеих точек (для start_point мы уже построили в предыдущем разделе), назовём их для различия Cumulative cost SP (start point) и Cumulative cost EP (end point). А теперь их просто складываем в калькуляторе растров:
"Cumulative cost SP@1" + "Cumulative cost EP@1"
Записываем результат в Cumulative_cost_both
Получается вот такая объединенная поверхность.
Теперь вспомним, сколько времени занимал оптимальный маршрут - порядка 860 минут. Допустим, мы готовы дать свободу в 40 дополнительных минут и посмотреть, в каких точках тогда можно будет наблюдать перемещение. То есть устанавливаем предельную цену в 900 (860+40) минут. В калькуляторе растров превратим Cumulative_cost_both в бинарный растр по порогу 900:
"Cumulative_cost_both@1" >= 900
Сохраним результат в corridor_900. Получился вот такой растр, у него в области коридора значения 0, а во всех остальных 1.
Теперь либо через стилизацию растра, либо через преобразование растра в вектор можно без труда получить карту и статистику по коридору. Давайте создадим вектор. Для это воспользуемся модулем Polygonize, который доступен в GDAL - Raster conversion - Polygonize в панели анализа
Из результирующего векторного слоя удаляем все объекты, у которых значение атрибута DN = 1
С оставшимися объектами получаем такую картину:
Заодно можем оценить площадь коридора: 1182 квадратных километра.
Заключение
Благодаря модулям GRASS в открытых ГИС доступны мощные инструменты для моделирования перемещений по пересеченной местности, которые можно гибко настраивать, использовать большое количество дополнительных данных и адаптировать под свои задачи. Все наиболее популярные задачи - построение изохрон, расчёт оптимальных маршрутов и коридоров наименьших затрат успешно решаются и могут быть, при необходимости, автоматизированы.
Дополнительные сведения
Для QGIS 2.* существует плагин Walking Time, использующий функцию Тоблера для построения маршрута.
Иногда при установке QGIS 3 под Windows из панели анализа недоступны инструменты SAGA. Для того, чтобы это исправить, можно установить QGIS через OSGeo4W Installer, выбрав в разделе desktop saga-ltr вместо saga по умолчанию.
Существует попытка переписать r.walk для моделирования по функции Тоблера, чтобы это работало честно в интерактивном режиме, а не с допущениями, принятыми нами. Познакомиться с кодом, чтобы попробовать собрать решение у себя на компьютере, вы можете здесь: https://github.com/fxi/AccessMod_r.walk