Задачи на сфере: угловая засечка: различия между версиями
ErnieBoyd (обсуждение | вклад) м (→Алгоритм) |
ErnieBoyd (обсуждение | вклад) м (→Алгоритм) |
||
| (не показано 18 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
{{Статья| | {{Статья|Опубликована|sphere-geodesic-angular-resection}} | ||
{{Аннотация| | {{Аннотация|Угловая засечка — это нахождение положения точки по координатам двух исходных пунктов и значениям азимутов направлений с этих пунктов на определяемую точку.}} | ||
== Общие положения == | == Общие положения == | ||
| Строка 25: | Строка 25: | ||
== Алгоритм == | == Алгоритм == | ||
[[Image: | [[Image:Sphere-task-angular.png|frame|c|right|Угловая засечка]] | ||
Решение любого вида засечек сводится к нахождению полярных координат искомой точки, т.е. начального направления и расстояния на неё с одного из исходных пунктов. На конечном этапе координаты находятся из решения прямой геодезической задачи. Поскольку в угловой засечке направления ''α''₁₃ и ''α''₂₃ уже заданы, остаётся определить расстояние ''σ''₁₃ или ''σ''₂₃. | Решение любого вида засечек сводится к нахождению полярных координат искомой точки, т.е. начального направления и расстояния на неё с одного из исходных пунктов. На конечном этапе координаты находятся из решения прямой геодезической задачи. Поскольку в угловой засечке направления ''α''₁₃ и ''α''₂₃ уже заданы, остаётся определить расстояние ''σ''₁₃ или ''σ''₂₃. | ||
На рисунке синим цветом выделены заданные элементы | На рисунке синим цветом выделены заданные элементы сферических треугольников, красным цветом неизвестные, зелёным — вспомогательные элементы. Очевидно, в треугольнике ''Q''₁''Q''₂''Q''₃ нет ни одного известного элемента. Однако из решения обратной геодезической задачи для пунктов ''Q''₁, ''Q''₂ могут быть получены расстояние ''σ''₁₂, а также азимуты ''α''₁₂ и ''α''₂₁, после чего углы ''β''₁ и ''β''₂ вычисляются как разности азимутов при соответствующих пунктах. Далее из решения треугольника ''Q''₁''Q''₂''Q''₃ найдём сторону ''σ''₁₃. | ||
'''Последовательность действий:''' | '''Последовательность действий:''' | ||
| Строка 37: | Строка 37: | ||
# решить прямую геодезическую задачу для ''Q''₁, ''Q''₃: по ''φ''₁, ''λ''₁, ''α''₁₃, ''σ''₁₃ вычислить ''φ''₃, ''λ''₃. | # решить прямую геодезическую задачу для ''Q''₁, ''Q''₃: по ''φ''₁, ''λ''₁, ''α''₁₃, ''σ''₁₃ вычислить ''φ''₃, ''λ''₃. | ||
Действия по первому и последнему пунктам рассмотрены в статьях [ | Действия по первому и последнему пунктам рассмотрены в статьях [http://gis-lab.info/qa/sphere-geodesic-invert-problem.html Задачи на сфере: обратная геодезическая задача] и [http://gis-lab.info/qa/sphere-geodesic-direct-problem.html Задачи на сфере: прямая геодезическая задача]. | ||
Углы ''β''₁, ''β''₂ и длина ''σ''₁₃ вычисляются по формулам: | Углы ''β''₁, ''β''₂ и длина ''σ''₁₃ вычисляются по формулам: | ||
: <math>\begin{ | : <math>\begin{align} | ||
\beta_1 & = | \beta_1 & = \alpha_{12} - \alpha_{13} \\ | ||
\beta_2 & = | \beta_2 & = \alpha_{23} - \alpha_{21} \\ | ||
\sigma_{13} & = | \sigma_{13} & = \operatorname{arctg\,} \dfrac{\sin \beta_2 \sin \sigma_{12}}{\cos \beta_2 \sin \beta_1 + \sin \beta_2 \cos \beta_1 \cos \sigma_{12}} | ||
\end{ | \end{align}</math> | ||
Правда, до вычисления длины ''σ''₁₃ необходимо проанализировать полученные значения углов ''β''₁ и ''β''₂. Ниже в коде функции можно увидеть пример такого анализа: | Правда, до вычисления длины ''σ''₁₃ необходимо проанализировать полученные значения углов ''β''₁ и ''β''₂. Ниже в коде функции можно увидеть пример такого анализа: | ||
| Строка 52: | Строка 52: | ||
* если линии ''Q''₁''Q''₃ и ''Q''₂''Q''₃ уходят в разные полушария от ''Q''₁''Q''₂, функция находит ближайшее к ''Q''₁''Q''₂ «ложное пересечение» этих линий. | * если линии ''Q''₁''Q''₃ и ''Q''₂''Q''₃ уходят в разные полушария от ''Q''₁''Q''₂, функция находит ближайшее к ''Q''₁''Q''₂ «ложное пересечение» этих линий. | ||
Здесь необходимо пояснить, что на сфере две несовпадающие геодезические линии всегда пересекаются в двух точках | Здесь необходимо пояснить, что на сфере две несовпадающие геодезические линии всегда пересекаются в двух точках-антиподах. В традиционной постановке задачи направление на нужное пересечение задаётся явно. Если же прямое и обратное направления по условию равнозначны, возникает вопрос выбора одного из антиподов: ''φ''₃, ''λ''₃ или ''φ''₃′ = −''φ''₃, ''λ''₃′ = ''λ''₃ ± 180°. | ||
== Пример программной реализации == | == Пример программной реализации == | ||
Пример функции <tt>SphereAngular</tt> на языке Си, реализующей вышеизоложенный алгоритм: | |||
<syntaxhighlight lang="c"> | |||
/* | |||
* Решение угловой засечки | |||
* | |||
* Аргументы исходные: | |||
* pt1 - {широта, долгота} пункта Q1 | |||
* pt2 - {широта, долгота} пункта Q2 | |||
* azi13 - азимут направления Q1-Q3 | |||
* azi23 - азимут направления Q2-Q3 | |||
* | |||
* Аргументы определяемые: | |||
* pt3 - {широта, долгота} точки Q3 | |||
*/ | |||
int SphereAngular(double pt1[], double pt2[], double azi13, double azi23, | |||
double pt3[]) | |||
{ | |||
double azi12, dist12, azi21, dist13; | |||
double cos_beta1, sin_beta1, cos_beta2, sin_beta2, cos_dist12, sin_dist12; | |||
SphereInverse(pt2, pt1, &azi21, &dist12); | |||
SphereInverse(pt1, pt2, &azi12, &dist12); | |||
cos_beta1 = cos(azi13 - azi12); | |||
sin_beta1 = sin(azi13 - azi12); | |||
cos_beta2 = cos(azi21 - azi23); | |||
sin_beta2 = sin(azi21 - azi23); | |||
cos_dist12 = cos(dist12); | |||
sin_dist12 = sin(dist12); | |||
if (sin_beta1 == 0. && sin_beta2 == 0.) // Решение - любая точка | |||
return -1; // на большом круге Q1-Q2. | |||
else if (sin_beta1 == 0.) { | |||
pt3[0] = pt2[0]; // Решение - точка Q2. | |||
pt3[1] = pt2[1]; | |||
return 0; | |||
} else if (sin_beta2 == 0.) { // Решение - точка Q1. | |||
pt3[0] = pt1[0]; | |||
pt3[1] = pt1[1]; | |||
return 0; | |||
} else if (sin_beta1 * sin_beta2 < 0.) { // Лучи Q1-Q3 и Q2-Q3 направлены | |||
if (fabs(sin_beta1) >= fabs(sin_beta2)) { // в разные полусферы. | |||
cos_beta2 = -cos_beta2; // Выберем ближайшее решение: | |||
sin_beta2 = -sin_beta2; // развернём луч Q2-Q3 на 180°; | |||
} else { // иначе | |||
cos_beta1 = -cos_beta1; // развернём луч Q1-Q3 на 180°. | |||
sin_beta1 = -sin_beta1; | |||
} | |||
} | |||
dist13 = atan2(fabs(sin_beta2) * sin_dist12, | |||
cos_beta2 * fabs(sin_beta1) | |||
+ fabs(sin_beta2) * cos_beta1 * cos_dist12); | |||
SphereDirect(pt1, azi13, dist13, pt3); | |||
return 0; | |||
} | |||
</syntaxhighlight> | |||
Этот код находится в архиве [[Медиа:Sph.zip|Sph.zip]] в файле '''sph.c'''. Кроме того, в файл '''sph.h''' включены следующие определения: | |||
<syntaxhighlight lang="c"> | |||
#define A_E 6371.0 // радиус Земли в километрах | |||
#define Degrees(x) (x * 57.29577951308232) // радианы -> градусы | |||
#define Radians(x) (x / 57.29577951308232) // градусы -> радианы | |||
</syntaxhighlight> | |||
Теперь напишем программу, которая обращается к функции <tt>SphereAngular</tt> для решения угловой засечки: | |||
<syntaxhighlight lang="c"> | |||
#include <stdio.h> | |||
#include <stdlib.h> | |||
#include "sph.h" | |||
int main(int argc, char *argv[]) | |||
{ | |||
char buf[1024]; | |||
double pt1[2], pt2[2], pt3[2]; | |||
double lat1, lon1, lat2, lon2, azi13, azi23; | |||
while (fgets(buf, 1024, stdin) != NULL) { | |||
sscanf(buf, "%lf %lf %lf %lf %lf %lf", | |||
&lat1, &lon1, &lat2, &lon2, &azi13, &azi23); | |||
pt1[0] = Radians(lat1); | |||
pt1[1] = Radians(lon1); | |||
pt2[0] = Radians(lat2); | |||
pt2[1] = Radians(lon2); | |||
if (SphereAngular(pt1, pt2, Radians(azi13), Radians(azi23), pt3)) | |||
puts("\t"); /* Бесконечно много решений на большом круге Q1-Q2 */ | |||
else | |||
printf("%f\t%f\n", Degrees(pt3[0]), Degrees(pt3[1])); | |||
} | |||
return 0; | |||
} | |||
</syntaxhighlight> | |||
В архиве [[Медиа:Sph.zip|Sph.zip]] этот код находится в файле '''ang.c'''. Создадим исполняемый модуль '''ang''' компилятором '''gcc''': | |||
<syntaxhighlight lang="bash"> | |||
$ gcc -o ang ang.c sph.c -lm | |||
</syntaxhighlight> | |||
Впрочем, в архиве есть '''Makefile'''. Для MS Windows готовую программу '''ang.exe''' можно найти в архиве [[Медиа:Sph-win32.zip|Sph-win32.zip]]. | |||
Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и «<» соответственно. Из каждой строки ввода программа считывает координаты первого и второго пунктов ''φ''₁, ''λ''₁, ''φ''₂, ''λ''₂, начальные азимуты ''α''₁₃ и ''α''₂₃ в градусах; решает угловую засечку; выводит в строку вывода координаты третьей точки ''φ''₃, ''λ''₃ в градусах. | |||
Создадим файл '''ang.dat''', содержащий одну строку данных: | |||
<pre> | |||
30 0 60 30 44.80406 110.389945 | |||
</pre> | |||
После запуска программы | |||
<syntaxhighlight lang="bash"> | |||
$ ang < ang.dat | |||
</syntaxhighlight> | |||
получим ''φ''₃, ''λ''₃: | |||
<pre> | |||
52.000000 54.000000 | |||
</pre> | |||
В архиве [[Медиа:Sph-py.zip|Sph-py.zip]] находится код на языке Питон. Выполнение скрипта в командной консоли: | |||
<syntaxhighlight lang="bash"> | |||
$ python ang.py ang.dat | |||
</syntaxhighlight> | |||
== Ссылки == | == Ссылки == | ||
* [ | * [http://gis-lab.info/qa/great-circles.html Вычисление расстояния и начального азимута между двумя точками на сфере] | ||
* [http://gis-lab.info/qa/biangulation.html Нахождение точки пересечения двух линий по углам и двум известным точкам (биангуляция)] | * [http://gis-lab.info/qa/biangulation.html Нахождение точки пересечения двух линий по углам и двум известным точкам (биангуляция)] | ||
* [http://gis-lab.info/qa/sphere-geodesic-invert-problem.html Задачи на сфере: обратная геодезическая задача] | |||
* [http://gis-lab.info/qa/sphere-geodesic-direct-problem.html Задачи на сфере: прямая геодезическая задача] | |||
* [http://gis-lab.info/qa/sphere-geodesic-linear-resection.html Задачи на сфере: линейная засечка] | |||
* [http://www.pm298.ru/sferich.php Краткий справочник по сферической тригонометрии] | |||
* [http://en.wikipedia.org/wiki/Earth_radius Earth radius] | |||
* [http://gis-lab.info/docs/books/sphere-trigonometry/sphere-trigonometry.rar Степанов Н. Н. Сферическая тригонометрия] | |||
Текущая версия от 08:41, 21 июня 2014
по адресу http://gis-lab.info/qa/sphere-geodesic-angular-resection.html
Угловая засечка — это нахождение положения точки по координатам двух исходных пунктов и значениям азимутов направлений с этих пунктов на определяемую точку.
Общие положения
В качестве модели Земли принимается сфера с радиусом R, равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга.
Введём следующие обозначения:
- φ — географическая широта,
- λ — географическая долгота,
- α — азимут дуги большого круга,
- σ — сферическое расстояние (длина дуги большого круга, выраженная в долях радиуса шара).
Линейное расстояние по дуге большого круга s связано со сферическим расстоянием σ формулой s = R σ.
Постановка задачи
- Исходные данные
- координаты пунктов Q₁, Q₂ — φ₁, λ₁, φ₂, λ₂,
- начальные направления с пунктов Q₁, Q₂ на точку Q₃ — α₁₃, α₂₃.
- Определяемые величины
- координаты точки Q₃ — φ₃, λ₃.
Алгоритм
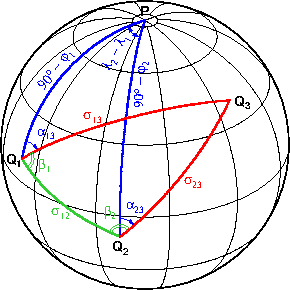
Решение любого вида засечек сводится к нахождению полярных координат искомой точки, т.е. начального направления и расстояния на неё с одного из исходных пунктов. На конечном этапе координаты находятся из решения прямой геодезической задачи. Поскольку в угловой засечке направления α₁₃ и α₂₃ уже заданы, остаётся определить расстояние σ₁₃ или σ₂₃.
На рисунке синим цветом выделены заданные элементы сферических треугольников, красным цветом неизвестные, зелёным — вспомогательные элементы. Очевидно, в треугольнике Q₁Q₂Q₃ нет ни одного известного элемента. Однако из решения обратной геодезической задачи для пунктов Q₁, Q₂ могут быть получены расстояние σ₁₂, а также азимуты α₁₂ и α₂₁, после чего углы β₁ и β₂ вычисляются как разности азимутов при соответствующих пунктах. Далее из решения треугольника Q₁Q₂Q₃ найдём сторону σ₁₃.
Последовательность действий:
- решить обратную геодезическую задачу для Q₁, Q₂: по φ₁, λ₁, φ₂, λ₂ получить α₁₂, α₂₁, σ₁₂;
- вычислить углы β₁, β₂;
- в треугольнике Q₁Q₂Q₃ по σ₁₂, β₁, β₂ вычислить σ₁₃;
- решить прямую геодезическую задачу для Q₁, Q₃: по φ₁, λ₁, α₁₃, σ₁₃ вычислить φ₃, λ₃.
Действия по первому и последнему пунктам рассмотрены в статьях Задачи на сфере: обратная геодезическая задача и Задачи на сфере: прямая геодезическая задача.
Углы β₁, β₂ и длина σ₁₃ вычисляются по формулам:
Правда, до вычисления длины σ₁₃ необходимо проанализировать полученные значения углов β₁ и β₂. Ниже в коде функции можно увидеть пример такого анализа:
- если линии Q₁Q₃ и Q₂Q₃ совпадают с Q₁Q₂, решение не определено, т.к. решением может быть любая точка геодезической линии Q₁Q₂;
- если одна из линий Q₁Q₃ и Q₂Q₃ совпадает с Q₁Q₂, а другая нет, решением является пункт, из которого выходит другая;
- если линии Q₁Q₃ и Q₂Q₃ уходят в разные полушария от Q₁Q₂, функция находит ближайшее к Q₁Q₂ «ложное пересечение» этих линий.
Здесь необходимо пояснить, что на сфере две несовпадающие геодезические линии всегда пересекаются в двух точках-антиподах. В традиционной постановке задачи направление на нужное пересечение задаётся явно. Если же прямое и обратное направления по условию равнозначны, возникает вопрос выбора одного из антиподов: φ₃, λ₃ или φ₃′ = −φ₃, λ₃′ = λ₃ ± 180°.
Пример программной реализации
Пример функции SphereAngular на языке Си, реализующей вышеизоложенный алгоритм:
/*
* Решение угловой засечки
*
* Аргументы исходные:
* pt1 - {широта, долгота} пункта Q1
* pt2 - {широта, долгота} пункта Q2
* azi13 - азимут направления Q1-Q3
* azi23 - азимут направления Q2-Q3
*
* Аргументы определяемые:
* pt3 - {широта, долгота} точки Q3
*/
int SphereAngular(double pt1[], double pt2[], double azi13, double azi23,
double pt3[])
{
double azi12, dist12, azi21, dist13;
double cos_beta1, sin_beta1, cos_beta2, sin_beta2, cos_dist12, sin_dist12;
SphereInverse(pt2, pt1, &azi21, &dist12);
SphereInverse(pt1, pt2, &azi12, &dist12);
cos_beta1 = cos(azi13 - azi12);
sin_beta1 = sin(azi13 - azi12);
cos_beta2 = cos(azi21 - azi23);
sin_beta2 = sin(azi21 - azi23);
cos_dist12 = cos(dist12);
sin_dist12 = sin(dist12);
if (sin_beta1 == 0. && sin_beta2 == 0.) // Решение - любая точка
return -1; // на большом круге Q1-Q2.
else if (sin_beta1 == 0.) {
pt3[0] = pt2[0]; // Решение - точка Q2.
pt3[1] = pt2[1];
return 0;
} else if (sin_beta2 == 0.) { // Решение - точка Q1.
pt3[0] = pt1[0];
pt3[1] = pt1[1];
return 0;
} else if (sin_beta1 * sin_beta2 < 0.) { // Лучи Q1-Q3 и Q2-Q3 направлены
if (fabs(sin_beta1) >= fabs(sin_beta2)) { // в разные полусферы.
cos_beta2 = -cos_beta2; // Выберем ближайшее решение:
sin_beta2 = -sin_beta2; // развернём луч Q2-Q3 на 180°;
} else { // иначе
cos_beta1 = -cos_beta1; // развернём луч Q1-Q3 на 180°.
sin_beta1 = -sin_beta1;
}
}
dist13 = atan2(fabs(sin_beta2) * sin_dist12,
cos_beta2 * fabs(sin_beta1)
+ fabs(sin_beta2) * cos_beta1 * cos_dist12);
SphereDirect(pt1, azi13, dist13, pt3);
return 0;
}
Этот код находится в архиве Sph.zip в файле sph.c. Кроме того, в файл sph.h включены следующие определения:
#define A_E 6371.0 // радиус Земли в километрах
#define Degrees(x) (x * 57.29577951308232) // радианы -> градусы
#define Radians(x) (x / 57.29577951308232) // градусы -> радианы
Теперь напишем программу, которая обращается к функции SphereAngular для решения угловой засечки:
#include <stdio.h>
#include <stdlib.h>
#include "sph.h"
int main(int argc, char *argv[])
{
char buf[1024];
double pt1[2], pt2[2], pt3[2];
double lat1, lon1, lat2, lon2, azi13, azi23;
while (fgets(buf, 1024, stdin) != NULL) {
sscanf(buf, "%lf %lf %lf %lf %lf %lf",
&lat1, &lon1, &lat2, &lon2, &azi13, &azi23);
pt1[0] = Radians(lat1);
pt1[1] = Radians(lon1);
pt2[0] = Radians(lat2);
pt2[1] = Radians(lon2);
if (SphereAngular(pt1, pt2, Radians(azi13), Radians(azi23), pt3))
puts("\t"); /* Бесконечно много решений на большом круге Q1-Q2 */
else
printf("%f\t%f\n", Degrees(pt3[0]), Degrees(pt3[1]));
}
return 0;
}
В архиве Sph.zip этот код находится в файле ang.c. Создадим исполняемый модуль ang компилятором gcc:
$ gcc -o ang ang.c sph.c -lm
Впрочем, в архиве есть Makefile. Для MS Windows готовую программу ang.exe можно найти в архиве Sph-win32.zip.
Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и «<» соответственно. Из каждой строки ввода программа считывает координаты первого и второго пунктов φ₁, λ₁, φ₂, λ₂, начальные азимуты α₁₃ и α₂₃ в градусах; решает угловую засечку; выводит в строку вывода координаты третьей точки φ₃, λ₃ в градусах.
Создадим файл ang.dat, содержащий одну строку данных:
30 0 60 30 44.80406 110.389945
После запуска программы
$ ang < ang.dat
получим φ₃, λ₃:
52.000000 54.000000
В архиве Sph-py.zip находится код на языке Питон. Выполнение скрипта в командной консоли:
$ python ang.py ang.dat
Ссылки
- Вычисление расстояния и начального азимута между двумя точками на сфере
- Нахождение точки пересечения двух линий по углам и двум известным точкам (биангуляция)
- Задачи на сфере: обратная геодезическая задача
- Задачи на сфере: прямая геодезическая задача
- Задачи на сфере: линейная засечка
- Краткий справочник по сферической тригонометрии
- Earth radius
- Степанов Н. Н. Сферическая тригонометрия