Задачи на сфере: прямая геодезическая задача: различия между версиями
ErnieBoyd (обсуждение | вклад) |
|||
| (не показаны 62 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
{{Статья| | {{Статья|Опубликована|sphere-geodesic-direct-problem}} | ||
{{Аннотация|Прямая геодезическая задача — это нахождение положения точки по координатам исходного пункта и значениям начального направления и расстояния.}} | {{Аннотация|Прямая геодезическая задача — это нахождение положения точки по координатам исходного пункта и значениям начального направления и расстояния.}} | ||
| Строка 5: | Строка 5: | ||
== Общие положения == | == Общие положения == | ||
В качестве модели Земли принимается сфера с радиусом ''R'', равным среднему радиусу земного эллипсоида. Введём следующие обозначения: | В качестве модели Земли принимается сфера с радиусом ''R'', равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга. | ||
Введём следующие обозначения: | |||
* ''φ'' — географическая широта, | * ''φ'' — географическая широта, | ||
* ''λ'' — географическая долгота, | * ''λ'' — географическая долгота, | ||
| Строка 17: | Строка 19: | ||
== Постановка задачи == | == Постановка задачи == | ||
[[Image: | [[Image:Sphere-task-direct.png|frame|c|right|Прямая геодезическая задача]] | ||
; Исходные данные | ; Исходные данные | ||
: координаты пункта ''Q''₁, начальное направление и расстояние на сфере — ''φ''₁, ''λ''₁, ''α''₁, ''σ''. | : координаты пункта ''Q''₁, начальное направление и расстояние на сфере — ''φ''₁, ''λ''₁, ''α''₁, ''σ''. | ||
; Определяемые величины | ; Определяемые величины | ||
: координаты пункта ''Q''₂ | : координаты пункта ''Q''₂ — ''φ''₂, ''λ''₂. | ||
На рисунке синим цветом выделены заданные элементы сферического треугольника, красным цветом неизвестные. | На рисунке синим цветом выделены заданные элементы сферического треугольника, красным цветом неизвестные. | ||
| Строка 28: | Строка 30: | ||
== Алгоритм == | == Алгоритм == | ||
Существует | Существует великое множество подходов к решению поставленной задачи. Рассмотрим простой и надёжный векторный метод. | ||
'''Последовательность решения''': | '''Последовательность решения''': | ||
# преобразовать углы ( | # преобразовать углы (90° − ''σ'') и (180° − ''α''₁) в декартовы координаты, | ||
# развернуть координатные оси на угол | # развернуть координатные оси вокруг оси ''Y'' на угол (''φ''₁ − 90°), | ||
# преобразовать декартовы координаты в сферические | # развернуть координатные оси вокруг оси ''Z'' на угол −''λ''₁, | ||
# преобразовать декартовы координаты в сферические. | |||
Если третий пункт пропустить, на выходе вместо долготы ''λ''₂ получится разность долгот (''λ''₂ − ''λ''₁), что упростит алгоритм. Останется только прибавить долготу первого пункта. С другой строны, благодаря третьему пункту долгота ''λ''₂ всегда будет в диапазоне [−180°, +180°]. | |||
Пример реализации алгоритма в виде функции языка Си: | Пример реализации алгоритма в виде функции языка Си: | ||
| Строка 43: | Строка 44: | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
/* | /* | ||
* Решение | * Решение прямой геодезической задачи | ||
* | * | ||
* Аргументы исходные: | * Аргументы исходные: | ||
* pt1 - {широта, долгота} точки | * pt1 - {широта, долгота} точки Q1 | ||
* | * azi - азимут начального направления | ||
* dist - расстояние (сферическое) | |||
* | * | ||
* Аргументы определяемые: | * Аргументы определяемые: | ||
* | * pt2 - {широта, долгота} точки Q2 | ||
*/ | */ | ||
void | void SphereDirect(double pt1[], double azi, double dist, double pt2[]) | ||
{ | { | ||
double | double pt[2], x[3]; | ||
SpherToCart( | pt[0] = M_PI_2 - dist; | ||
Rotate(x, pt1[ | pt[1] = M_PI - azi; | ||
Rotate(x, | SpherToCart(pt, x); // сферические -> декартовы | ||
CartToSpher(x, | Rotate(x, pt1[0] - M_PI_2, 1); // первое вращение | ||
Rotate(x, -pt1[1], 2); // второе вращение | |||
CartToSpher(x, pt2); // декартовы -> сферические | |||
return; | return; | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Следует заметить, что прямая и обратная задача математически идентичны, и алгоритмы их решения зеркально отражают друг друга. | Следует заметить, что прямая и обратная задача математически идентичны, и алгоритмы их решения зеркально отражают друг друга. | ||
| Строка 74: | Строка 73: | ||
=== Преобразование сферических координат в декартовы === | === Преобразование сферических координат в декартовы === | ||
: <math>\begin{ | : <math>\begin{align} | ||
x & = | x & = \cos \varphi \cos \lambda \\ | ||
y & = | y & = \cos \varphi \sin \lambda \\ | ||
z & = | z & = \sin \varphi | ||
\end{ | \end{align}</math> | ||
В данном случае в качестве сферических координат ''φ'', ''λ'' подставим углы (90° − ''σ''), (180° − ''α''₁). | |||
Реализация на Си: | Реализация на Си: | ||
| Строка 89: | Строка 90: | ||
* y - {широта, долгота} | * y - {широта, долгота} | ||
* | * | ||
* | * Аргументы определяемые: | ||
* x - вектор {x, y, z} | * x - вектор {x, y, z} | ||
*/ | */ | ||
| Строка 107: | Строка 108: | ||
=== Вращение вокруг оси === | === Вращение вокруг оси === | ||
Представим оператор вращения вокруг оси ''X'' на угол ''θ'' в следующем виде: | |||
: <math>\begin{ | : <math>\begin{align} | ||
x' & = | x' & = x \\ | ||
y' & = | y' & = y \cos \theta + z \sin \theta \\ | ||
z' & = | z' & = - y \sin \theta + z \cos \theta | ||
\end{ | \end{align}</math> | ||
Реализация вращения вокруг координатной оси на Си: | Операторы вращения вокруг осей ''Y'' и ''Z'' получаются перестановкой символов. | ||
Реализация вращения вокруг ''i''-ой координатной оси на Си: | |||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| Строка 145: | Строка 148: | ||
=== Преобразование декартовых координат в сферические === | === Преобразование декартовых координат в сферические === | ||
: <math>\begin{ | : <math>\begin{align} | ||
\ | \lambda & = \operatorname{arctg\,} \dfrac{y}{x} \\ | ||
\ | \varphi & = \operatorname{arctg\,} \dfrac{z}{\sqrt{x^2 + y^2}} | ||
\end{ | \end{align}</math> | ||
В данном случае в роли сферических координат ''φ'', ''λ'' окажутся ''φ''₂, ''λ''₂. | |||
Реализация на Си: | Реализация на Си: | ||
| Строка 169: | Строка 174: | ||
double p; | double p; | ||
p = | p = hypot(x[0], x[1]); | ||
y[1] = atan2(x[1], x[0]); | y[1] = atan2(x[1], x[0]); | ||
y[0] = atan2(x[2], p); | y[0] = atan2(x[2], p); | ||
return | return hypot(p, x[2]); | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Строка 179: | Строка 184: | ||
== Пример программной реализации == | == Пример программной реализации == | ||
Исходники вышеприведённых функций можно найти в архиве [[Медиа:Sph. | Исходники вышеприведённых функций можно найти в архиве [[Медиа:Sph.zip|Sph.zip]] в файле '''sph.c'''. Кроме того, в файл '''sph.h''' включены следующие определения: | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| Строка 187: | Строка 192: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Теперь напишем программу, которая обращается к функции <tt> | Теперь напишем программу, которая обращается к функции <tt>SphereDirect</tt> для решения прямой задачи: | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| Строка 198: | Строка 203: | ||
char buf[1024]; | char buf[1024]; | ||
double pt1[2], pt2[2]; | double pt1[2], pt2[2]; | ||
double lat1, lon1, | double lat1, lon1, azi1, dist, azi2; | ||
while (fgets(buf, 1024, stdin) != NULL) { | while (fgets(buf, 1024, stdin) != NULL) { | ||
sscanf(buf, "%lf %lf %lf %lf", &lat1, &lon1, & | sscanf(buf, "%lf %lf %lf %lf", &lat1, &lon1, &azi1, &dist); | ||
pt1[0] = Radians(lat1); | pt1[0] = Radians(lat1); | ||
pt1[1] = Radians(lon1); | pt1[1] = Radians(lon1); | ||
SphereDirect(pt1, Radians(azi1), dist / A_E, pt2); // Решение прямой задачи | |||
SphereInverse(pt2, pt1, &azi2, &dist); // Вычисление обратного азимута | |||
SphereInverse(pt2, pt1, &azi2, &dist); | printf("%f\t%f\t%f\n", Degrees(pt2[0]), Degrees(pt2[1]), Degrees(azi2)); | ||
printf("%f\t%f\t% | |||
} | } | ||
return 0; | return 0; | ||
| Строка 214: | Строка 217: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
В архиве [[Медиа:Sph. | В архиве [[Медиа:Sph.zip|Sph.zip]] этот код находится в файле '''dir.c'''. Создадим исполняемый модуль '''dir''' компилятором '''gcc''': | ||
<syntaxhighlight lang="bash"> | <syntaxhighlight lang="bash"> | ||
$ gcc -o | $ gcc -o dir dir.c sph.c -lm | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Для MS Windows готовую программу ''' | Впрочем, в архиве есть '''Makefile'''. Для MS Windows готовую программу '''dir.exe''' можно найти в архиве [[Медиа:Sph-win32.zip|Sph-win32.zip]]. | ||
Программа читает данные | Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и «<» соответственно. Из каждой строки ввода программа считывает координаты первого пункта ''φ''₁, ''λ''₁, начальный азимут ''α''₁ в градусах и расстояние ''s'' в километрах; решает прямую задачу; записывает в строку вывода координаты второго пункта ''φ''₂, ''λ''₂ и обратный азимут ''α''₂ в градусах. | ||
Создадим файл ''' | Создадим файл '''dir.dat''', содержащий одну строку данных: | ||
<pre> | <pre> | ||
30 0 | 30 0 44.804060 5001.1309 | ||
</pre> | </pre> | ||
| Строка 233: | Строка 236: | ||
<syntaxhighlight lang="bash"> | <syntaxhighlight lang="bash"> | ||
$ | $ dir < dir.dat | ||
</syntaxhighlight> | </syntaxhighlight> | ||
получим '' | получим ''φ''₂, ''λ''₂, ''α''₂: | ||
<pre> | <pre> | ||
52.000000 54.000001 262.415109 | |||
</pre> | </pre> | ||
В архиве [[Медиа:Sph-py.zip|Sph-py.zip]] находятся скрипты на языке Питон. Выполнение скрипта в командной консоли: | |||
В пакет PROJ | <syntaxhighlight lang="bash"> | ||
$ python dir.py dir.dat | |||
</syntaxhighlight> | |||
== Решение прямой задачи средствами PROJ == | |||
В пакет PROJ входит программа '''geod''', предназначенная для решения прямых и обратных геодезических задач на сфере. Так выглядит команда обработки файла '''dir.dat''': | |||
<syntaxhighlight lang="bash"> | <syntaxhighlight lang="bash"> | ||
$ geod +a=6371000 | $ geod +a=6371000 +b=6371000 -f "%f" +units=km dir.dat | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Параметр <tt>+a</tt> определяет радиус сферы | Параметр <tt>+a</tt> определяет радиус сферы, <tt>-f</tt> — формат вывода угловых величин, <tt>+units</tt> — единица измерения расстояний. В итоге получим идентичный результат: | ||
<pre> | <pre> | ||
52.000000 54.000001 -97.584891 | |||
</pre> | </pre> | ||
Различие значений ''α''₂ на 360° объясняется тем, что ''' | Различие значений ''α''₂ на 360° объясняется тем, что '''dir''' выводит азимуты в диапазоне от 0° до 360°, а '''geod''' от −180° до +180°. | ||
С помощью '''geod''' можно также расставить промежуточные точки вдоль геодезической линии либо по дуге малого круга на заданном расстоянии от исходного пункта. В обоих случаях нужно задать положение начальной точки параметрами <tt>+lat_1</tt>, <tt>+lon_1</tt> и либо координаты второй точки <tt>+lat_2</tt>, <tt>+lon_1</tt>, либо расстояние и азимут ко второй точке <tt>+S</tt>, <tt>+A</tt>. За подробностями обращайтесь к [http://trac.osgeo.org/proj/wiki/man_geod документации]. | |||
== Альтернативные методы == | == Альтернативные методы == | ||
Большая часть других методов основана на сферической тригонометрии. Многие из них используют вычисление ''φ''₂ или (''λ''₂ − ''λ''₁) по таким функциям, как синус, косинус или гаверсинус. Это приводит к неоднозначности результатов вблизи особых значений, когда производная функции равна нулю. Такие методы не могут считаться универсальными. | |||
К наиболее надёжным относится следующий способ: | |||
<math>\begin{align} | |||
\xi & = \cos \sigma \cos \varphi_1 - \sin \sigma \sin \varphi_1 \cos \alpha_1 \\ | |||
\eta & = \sin \sigma \sin \alpha_1 \\ | |||
\operatorname{tg\,} (\lambda_2 - \lambda_1) & = \dfrac{\eta}{\xi} \\ | |||
\operatorname{tg\,} \varphi_2 & = \dfrac{\sin \varphi_1 \cos \sigma + \cos \varphi_1 \sin \sigma \cos \alpha_1}{\xi \cos (\lambda_2 - \lambda_1) + \eta \sin (\lambda_2 - \lambda_1)} | |||
\end{align}</math> | |||
В сферической тригонометрии углы и стороны должны быть в диапазоне [0, 180°]. Алгоритмизация формул требует анализа и обработки случаев, когда входные величины не попадают в эти рамки. | |||
== Ссылки == | == Ссылки == | ||
* [ | * [http://gis-lab.info/qa/great-circles.html Вычисление расстояния и начального азимута между двумя точками на сфере] | ||
* [http://gis-lab.info/qa/sphere-geodesic-invert-problem.html Задачи на сфере: обратная геодезическая задача] | |||
* [http://gis-lab.info/qa/sphere-geodesic-angular-resection.html Задачи на сфере: угловая засечка] | |||
* [http://gis-lab.info/qa/sphere-geodesic-linear-resection.html Задачи на сфере: линейная засечка] | |||
* [http://www.pm298.ru/sferich.php Краткий справочник по сферической тригонометрии] | |||
* [http://trac.osgeo.org/proj/wiki/man_geod man_geod – PROJ.4] | |||
* [http://en.wikipedia.org/wiki/Earth_radius Earth radius] | |||
* [http://gis-lab.info/docs/books/sphere-trigonometry/sphere-trigonometry.rar Степанов Н. Н. Сферическая тригонометрия] | * [http://gis-lab.info/docs/books/sphere-trigonometry/sphere-trigonometry.rar Степанов Н. Н. Сферическая тригонометрия] | ||
Текущая версия от 06:46, 10 мая 2020
по адресу http://gis-lab.info/qa/sphere-geodesic-direct-problem.html
Прямая геодезическая задача — это нахождение положения точки по координатам исходного пункта и значениям начального направления и расстояния.
Общие положения
В качестве модели Земли принимается сфера с радиусом R, равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга.
Введём следующие обозначения:
- φ — географическая широта,
- λ — географическая долгота,
- α — азимут дуги большого круга,
- σ — сферическое расстояние (длина дуги большого круга, выраженная в долях радиуса шара).
Линейное расстояние по дуге большого круга s связано со сферическим расстоянием σ формулой s = R σ.
Прямая и обратная геодезические задачи являются важными элементами более сложных геодезических задач.
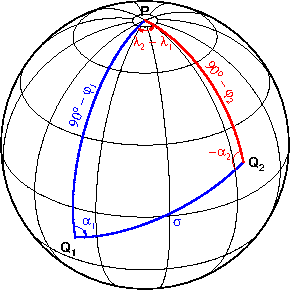
Постановка задачи
- Исходные данные
- координаты пункта Q₁, начальное направление и расстояние на сфере — φ₁, λ₁, α₁, σ.
- Определяемые величины
- координаты пункта Q₂ — φ₂, λ₂.
На рисунке синим цветом выделены заданные элементы сферического треугольника, красным цветом неизвестные.
Алгоритм
Существует великое множество подходов к решению поставленной задачи. Рассмотрим простой и надёжный векторный метод.
Последовательность решения:
- преобразовать углы (90° − σ) и (180° − α₁) в декартовы координаты,
- развернуть координатные оси вокруг оси Y на угол (φ₁ − 90°),
- развернуть координатные оси вокруг оси Z на угол −λ₁,
- преобразовать декартовы координаты в сферические.
Если третий пункт пропустить, на выходе вместо долготы λ₂ получится разность долгот (λ₂ − λ₁), что упростит алгоритм. Останется только прибавить долготу первого пункта. С другой строны, благодаря третьему пункту долгота λ₂ всегда будет в диапазоне [−180°, +180°].
Пример реализации алгоритма в виде функции языка Си:
/*
* Решение прямой геодезической задачи
*
* Аргументы исходные:
* pt1 - {широта, долгота} точки Q1
* azi - азимут начального направления
* dist - расстояние (сферическое)
*
* Аргументы определяемые:
* pt2 - {широта, долгота} точки Q2
*/
void SphereDirect(double pt1[], double azi, double dist, double pt2[])
{
double pt[2], x[3];
pt[0] = M_PI_2 - dist;
pt[1] = M_PI - azi;
SpherToCart(pt, x); // сферические -> декартовы
Rotate(x, pt1[0] - M_PI_2, 1); // первое вращение
Rotate(x, -pt1[1], 2); // второе вращение
CartToSpher(x, pt2); // декартовы -> сферические
return;
}
Следует заметить, что прямая и обратная задача математически идентичны, и алгоритмы их решения зеркально отражают друг друга.
Преобразование сферических координат в декартовы
В данном случае в качестве сферических координат φ, λ подставим углы (90° − σ), (180° − α₁).
Реализация на Си:
/*
* Преобразование сферических координат в вектор
*
* Аргументы исходные:
* y - {широта, долгота}
*
* Аргументы определяемые:
* x - вектор {x, y, z}
*/
void SpherToCart(double y[], double x[])
{
double p;
p = cos(y[0]);
x[2] = sin(y[0]);
x[1] = p * sin(y[1]);
x[0] = p * cos(y[1]);
return;
}
Вращение вокруг оси
Представим оператор вращения вокруг оси X на угол θ в следующем виде:
Операторы вращения вокруг осей Y и Z получаются перестановкой символов.
Реализация вращения вокруг i-ой координатной оси на Си:
/*
* Вращение вокруг координатной оси
*
* Аргументы:
* x - входной/выходной 3-вектор
* a - угол вращения
* i - номер координатной оси (0..2)
*/
void Rotate(double x[], double a, int i)
{
double c, s, xj;
int j, k;
j = (i + 1) % 3;
k = (i - 1) % 3;
c = cos(a);
s = sin(a);
xj = x[j] * c + x[k] * s;
x[k] = -x[j] * s + x[k] * c;
x[j] = xj;
return;
}
Преобразование декартовых координат в сферические
В данном случае в роли сферических координат φ, λ окажутся φ₂, λ₂.
Реализация на Си:
/*
* Преобразование вектора в сферические координаты
*
* Аргументы исходные:
* x - {x, y, z}
*
* Аргументы определяемые:
* y - {широта, долгота}
*
* Возвращает:
* длину вектора
*/
double CartToSpher(double x[], double y[])
{
double p;
p = hypot(x[0], x[1]);
y[1] = atan2(x[1], x[0]);
y[0] = atan2(x[2], p);
return hypot(p, x[2]);
}
Пример программной реализации
Исходники вышеприведённых функций можно найти в архиве Sph.zip в файле sph.c. Кроме того, в файл sph.h включены следующие определения:
#define A_E 6371.0 // радиус Земли в километрах
#define Degrees(x) (x * 57.29577951308232) // радианы -> градусы
#define Radians(x) (x / 57.29577951308232) // градусы -> радианы
Теперь напишем программу, которая обращается к функции SphereDirect для решения прямой задачи:
#include <stdio.h>
#include <stdlib.h>
#include "sph.h"
int main(int argc, char *argv[])
{
char buf[1024];
double pt1[2], pt2[2];
double lat1, lon1, azi1, dist, azi2;
while (fgets(buf, 1024, stdin) != NULL) {
sscanf(buf, "%lf %lf %lf %lf", &lat1, &lon1, &azi1, &dist);
pt1[0] = Radians(lat1);
pt1[1] = Radians(lon1);
SphereDirect(pt1, Radians(azi1), dist / A_E, pt2); // Решение прямой задачи
SphereInverse(pt2, pt1, &azi2, &dist); // Вычисление обратного азимута
printf("%f\t%f\t%f\n", Degrees(pt2[0]), Degrees(pt2[1]), Degrees(azi2));
}
return 0;
}
В архиве Sph.zip этот код находится в файле dir.c. Создадим исполняемый модуль dir компилятором gcc:
$ gcc -o dir dir.c sph.c -lm
Впрочем, в архиве есть Makefile. Для MS Windows готовую программу dir.exe можно найти в архиве Sph-win32.zip.
Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и «<» соответственно. Из каждой строки ввода программа считывает координаты первого пункта φ₁, λ₁, начальный азимут α₁ в градусах и расстояние s в километрах; решает прямую задачу; записывает в строку вывода координаты второго пункта φ₂, λ₂ и обратный азимут α₂ в градусах.
Создадим файл dir.dat, содержащий одну строку данных:
30 0 44.804060 5001.1309
После запуска программы
$ dir < dir.dat
получим φ₂, λ₂, α₂:
52.000000 54.000001 262.415109
В архиве Sph-py.zip находятся скрипты на языке Питон. Выполнение скрипта в командной консоли:
$ python dir.py dir.dat
Решение прямой задачи средствами PROJ
В пакет PROJ входит программа geod, предназначенная для решения прямых и обратных геодезических задач на сфере. Так выглядит команда обработки файла dir.dat:
$ geod +a=6371000 +b=6371000 -f "%f" +units=km dir.dat
Параметр +a определяет радиус сферы, -f — формат вывода угловых величин, +units — единица измерения расстояний. В итоге получим идентичный результат:
52.000000 54.000001 -97.584891
Различие значений α₂ на 360° объясняется тем, что dir выводит азимуты в диапазоне от 0° до 360°, а geod от −180° до +180°.
С помощью geod можно также расставить промежуточные точки вдоль геодезической линии либо по дуге малого круга на заданном расстоянии от исходного пункта. В обоих случаях нужно задать положение начальной точки параметрами +lat_1, +lon_1 и либо координаты второй точки +lat_2, +lon_1, либо расстояние и азимут ко второй точке +S, +A. За подробностями обращайтесь к документации.
Альтернативные методы
Большая часть других методов основана на сферической тригонометрии. Многие из них используют вычисление φ₂ или (λ₂ − λ₁) по таким функциям, как синус, косинус или гаверсинус. Это приводит к неоднозначности результатов вблизи особых значений, когда производная функции равна нулю. Такие методы не могут считаться универсальными.
К наиболее надёжным относится следующий способ:
В сферической тригонометрии углы и стороны должны быть в диапазоне [0, 180°]. Алгоритмизация формул требует анализа и обработки случаев, когда входные величины не попадают в эти рамки.
Ссылки
- Вычисление расстояния и начального азимута между двумя точками на сфере
- Задачи на сфере: обратная геодезическая задача
- Задачи на сфере: угловая засечка
- Задачи на сфере: линейная засечка
- Краткий справочник по сферической тригонометрии
- man_geod – PROJ.4
- Earth radius
- Степанов Н. Н. Сферическая тригонометрия