Основы конфигурирования тайловых сеток: различия между версиями
м (→Размер тайла) |
|||
| (не показаны 53 промежуточные версии 4 участников) | |||
| Строка 1: | Строка 1: | ||
{{Статья| | {{Статья|Опубликована|tile-matrix}} | ||
== Введение == | == Введение == | ||
| Строка 27: | Строка 27: | ||
=== Масштабные уровни (разрешения) === | === Масштабные уровни (разрешения) === | ||
После того, как мы определились с проекцией и охватом, необходимо разобраться с масштабными уровнями. Каждый масштабный уровень определяет разрешение с которым отрендерена карта на данном уровне, при этом количество таких уровней может быть произвольным. Величина разрешения, используемого на том или ином уровне также ничем не лимитирована. Разрешение показывает сколько единиц измерения координат исходных данных укладывается в одном пикселе отрендеренной карты. Таким образом в нашем случае (проекция UTM) единицы измерения разрешения - м/пиксел, в случае же работы с географическими системами координат это будут градус/пиксел. | После того, как мы определились с проекцией и охватом, необходимо разобраться с масштабными уровнями. Каждый масштабный уровень определяет разрешение с которым будет отрендерена карта на данном уровне, при этом количество таких уровней может быть произвольным. Величина разрешения, используемого на том или ином уровне также ничем не лимитирована. Разрешение показывает сколько единиц измерения координат исходных данных укладывается в одном пикселе отрендеренной карты. Таким образом в нашем случае (проекция UTM) единицы измерения разрешения - м/пиксел, в случае же работы с географическими системами координат это будут градус/пиксел. | ||
Предположим, мы хотим предоставить доступ к нашим данным, отрендеренным с разрешениями | Предположим, мы хотим предоставить доступ к нашим данным, отрендеренным с разрешениями R, равными 3000 и 1500 метров на пиксел. Посчитаем для этих разрешений размеры результирующей карты (w - ширина, h - высота): | ||
[[Файл:Zoom-level-0.png|211px|thumb|center|<center>3000 метров на пиксел</center>]] | [[Файл:Zoom-level-0.png|211px|thumb|center|<center>3000 метров на пиксел</center>]] | ||
| Строка 45: | Строка 45: | ||
</pre> | </pre> | ||
Как уже было отмечено выше, разрешение <math> | Как уже было отмечено выше, разрешение <math>z</math>-го масштабного уровня может быть произвольным, однако на практике наиболее распространённым является случай, когда разрешение <math>z</math>-го уровня <math>R_z</math> в 2 раза выше разрешения предыдущего <math>R_{z-1}</math>: | ||
<center><math> | <center><math>R_z=\frac{R_{z-1}}{2}</math></center> | ||
Разрешение 0-го (<math> | Разрешение 0-го (<math>z=0</math>) масштабного уровня может устанавливаться произвольно, но опять же на практике широкое распространение получил следующий подход. Считается, что на нулевом уровне должно быть такое разрешение, которое бы позволило уместить карту целиком в один тайл. Чтобы его рассчитать, нам необходимо определиться с размерами тайла. | ||
Размер тайла (ширина и высота) определяет объём информации, передаваемой одним тайлом. Очевидно, что чем больше геометрические размеры тайла, тем больший объём дискового пространства он занимает и тем дольше он будет передаваться клиенту. Чем меньше размер тайла, тем он быстрее может быть доставлен клиенту, но при этом возрастает количество запросов с серверу, что в конечном итоге приводит к еще более длительному процессу получения тайлов. Экспериментальным путём было установлено, что наиболее эффективный размер тайла - 256x256 пикселов. | Размер тайла (ширина и высота) определяет объём информации, передаваемой одним тайлом. Очевидно, что чем больше геометрические размеры тайла, тем больший объём дискового пространства он занимает и тем дольше он будет передаваться клиенту. Чем меньше размер тайла, тем он быстрее может быть доставлен клиенту, но при этом возрастает количество запросов с серверу, что в конечном итоге приводит к еще более длительному процессу получения тайлов. Экспериментальным путём было установлено, что наиболее эффективный размер тайла - 256x256 пикселов. | ||
| Строка 57: | Строка 55: | ||
[[Файл:Osm-tile-example.png|border|frame|<center>Тайл сервиса OpenStreetMap имеет размер 256x256 пикселов</center>]] | [[Файл:Osm-tile-example.png|border|frame|<center>Тайл сервиса OpenStreetMap имеет размер 256x256 пикселов</center>]] | ||
Вернёмся к нашей задаче определения разрешения 0-го уровня. Определим ширину ( | Вернёмся к нашей задаче определения разрешения 0-го уровня. Определим ширину (W) и высоту (H) карты в единицах измерения данных: | ||
<pre> | <pre> | ||
| Строка 68: | Строка 66: | ||
<pre>R0 = max(W,H)/256 = 633063/256 = 2472 (м/пиксел)</pre> | <pre>R0 = max(W,H)/256 = 633063/256 = 2472 (м/пиксел)</pre> | ||
Можно записать общую формулу расчета разрешения | Можно записать общую формулу расчета разрешения z-го уровня карты размером WxH с размером тайла 256x256 с учётом того, что разрешение каждого последующего масштабного уровня в 2 раза выше предыдущего: | ||
<center><math>R_z=\frac{max(W,H)}{256\cdot 2^z}</math></center> | |||
<center><math> | |||
=== Положение начала отсчёта тайловой сетки === | === Положение начала отсчёта тайловой сетки === | ||
| Строка 77: | Строка 74: | ||
Начало отсчёта тайловой сетки, задаваемое в единицах измерения исходных данных, определяет индексы тайлов, по которым они будут доступны. Согласно спецификации TMS начало отсчёта тайловой сетки может располагаться вне охвата карты. В этом случае тайл (0,0) может и не существовать, однако это достаточно экзотический случай. Наиболее распространённым является случай, когда начало отсчёта тайловой сетки совпадает с координатами левого нижнего угла охвата карты (minx, miny): | Начало отсчёта тайловой сетки, задаваемое в единицах измерения исходных данных, определяет индексы тайлов, по которым они будут доступны. Согласно спецификации TMS начало отсчёта тайловой сетки может располагаться вне охвата карты. В этом случае тайл (0,0) может и не существовать, однако это достаточно экзотический случай. Наиболее распространённым является случай, когда начало отсчёта тайловой сетки совпадает с координатами левого нижнего угла охвата карты (minx, miny): | ||
[[Файл: | [[Файл:Tms-scheme-original.png|467px|thumb|center|<center>Пример TMS-совместимой тайловой сетки: положение начала отсчёта совпадает с координатами левого нижнего угла охвата карты</center>]] | ||
Другой часто встречающийся случай (не согласующийся со спецификацией TMS) - это когда положение начала отсчета тайловой сетки помещается в левую верхнюю точку охвата карты (minx, maxy): | Другой часто встречающийся случай (не согласующийся со спецификацией TMS) - это когда положение начала отсчета тайловой сетки помещается в левую верхнюю точку охвата карты (minx, maxy): | ||
[[Файл: | [[Файл:Xyz-scheme-original.png|467px|thumb|center|<center>Пример TMS-несовместимой тайловой сетки: положение начала отсчёта помещается в левую верхнюю точку охвата карты (используется в Google Maps, OpenStreetMap)</center>]] | ||
Данный подход используется, например, в OpenStreetMap: | Данный подход используется, например, в OpenStreetMap: | ||
| Строка 91: | Строка 88: | ||
== Количество тайлов на различных масштабных уровнях == | == Количество тайлов на различных масштабных уровнях == | ||
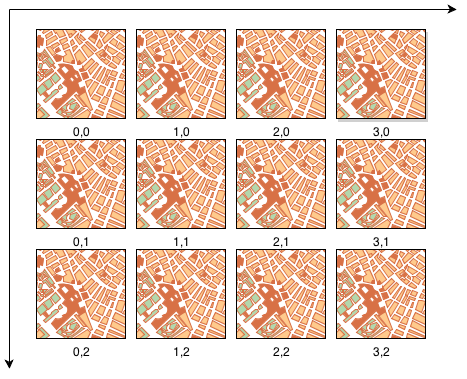
На основе вышесказанного можно легко оценить количество тайлов (x*y) на | На основе вышесказанного можно легко оценить количество тайлов (x*y) на z-м масштабном уровне. Количество столбцов тайлов (x) определяется соотношением: | ||
<pre>x = w/256 = W/( | <pre>x = w/256 = W/(Rz*256)</pre> | ||
Количество | Количество строк (y): | ||
<pre>y = h/256 = H/( | <pre>y = h/256 = H/(Rz*256)</pre> | ||
Вычислим количество тайлов, например, на 7 масштабном уровне с учётом, что зависимость разрешения от номера уровня задана функцией | Вычислим количество тайлов, например, на 7 масштабном уровне с учётом, что зависимость разрешения от номера уровня задана функцией, полученной в разделе [[#Масштабные уровни (разрешения)]]: | ||
<pre> | <pre> | ||
R7 = max(W,H)/(256*2^ | R7 = max(W,H)/(256*2^z) = 633063/(256*2^7) = 19.32 | ||
x = 633063/(19.32*256) = 128 | x = 633063/(19.32*256) = 128 | ||
y = 432725/(19.32*256) = 88 | y = 432725/(19.32*256) = 88 | ||
| Строка 196: | Строка 193: | ||
Так как в OpenStreetMap тайлы рендерятся только до 18 уровня, то получаем, что на последнем уровне количество тайлов достигает отметки 68 миллиардов. | Так как в OpenStreetMap тайлы рендерятся только до 18 уровня, то получаем, что на последнем уровне количество тайлов достигает отметки 68 миллиардов. | ||
== Подробнее о разрешениях == | |||
Строго говоря выражение "карта на таком-то масштабном уровне отрендерена с таким-то разрешением" в общем случае имеет слабую связь с реальными размерами элементов изображения на местности из-за непостоянства размеров вносимого проекционными искажениями. Покажем это на примере игры на базе данных Google Maps, использующих проекцию [http://spatialreference.org/ref/sr-org/7483/ Меркатора]. Среди разбросанных полигонов найдите соответствующий Австралии и оцените как изменяется его форма в области полюсов и на своём законном месте (полигоны можно двигать, цель игры - разместить контуры стран по своим местам): | |||
<center>{{#widget:Iframe | |||
|url=http://gmaps-samples.googlecode.com/svn/trunk/poly/puzzledrag.html | |||
|width=1024 | |||
|height=640 | |||
|border=0 | |||
}}</center> | |||
Изменение формы обусловлено выбранной проекцией - так в проекции Меркатора размеры элемента изображения карты не являются постоянными на местности. Линейные размеры увеличиваются от экватора к полюсам как обратный косинус широты ([http://ru.wikipedia.org/wiki/%CF%F0%EE%E5%EA%F6%E8%FF_%CC%E5%F0%EA%E0%F2%EE%F0%E0 Проекция Меркатора]). Таким образом, мы получаем, что пикселы даже в рамках одного тайла могут иметь различный размер: | |||
[[Файл:Osm-tile-example-0-0.png|256px|thumb|center|<center>Тайл сервиса OpenStreetMap на 0-м масштабном уровне. Как можно заметить размеры элементов в области полюсов значительно отличаются от их размеров на экваторе (Гренландия кажется в 2-3 раза больше Австралии, хотя в реальности Гренландия втрое меньше)</center>]] | |||
В общем случаем линейные размеры пиксела - это функция от его географических координат (<math>lat</math>, <math>lon</math>) и масштабного уровня: | |||
<center><math>R_z=f(lat,lon)\frac{\max(W,H)}{256\cdot 2^z}</math></center> | |||
В случае проекции Меркатора <math>f(lat,lon)=\cos(lat)</math>. С учётом этого выражение для вычисления разрешения принимает вид: | |||
<center><math>R_z=\cos(lat)\frac{\max(W,H)}{256\cdot 2^z}</math></center> | |||
Получается, что в сервисах, использующих проекцию Меркатора разрешение в области 60 широты в 2 раза выше разрешения на экваторе (в одном пикселе отрендеренной карты укладывается меньше единиц измерения координат исходных данных) и соответствует действительности как раз на экваторе. | |||
Тогда что-же мы подразумевали в предыдущих разделах данной статьи, говоря "разрешение z-го масштабного уровня"? Это ни что иное как некоторая абстрактная величина, имеющая размерность разрешения, которую удобно использовать для расчёта общего количества и координат тайлов. Если же мы хотим осуществлять измерения по нашей карте, то мы должны обязательно учитывать зависимость разрешения от географических координат. Выбрав в самом начале статьи проекцию UTM для рендеринга и заявив, что это "позволит нам осуществлять корректное измерение расстояний на полученной карте", мы обеспечили постоянство разрешения карты в пределах масштабного уровня, то есть независимость от географических координат: <math>f(lat,lon)=1</math>. | |||
== Понятие экранного масштаба карты == | |||
Экранный масштаб карты (S) показывает сколько единиц измерения на местности укладывается в единицу измерения карты на экране монитора и равен произведению разрешения карты на разрешение экрана (dots per inch, DPI) и на количество единиц карты в одной единице измерения разрешения экрана (inches per map unit, IPMU): | |||
<center><math>S_z=R_z \cdot DPI \cdot IPMU</math></center> | |||
Как было показано выше - разные области карты могут иметь различное разрешение, а, следовательно, и масштаб. | |||
== Ссылки == | == Ссылки == | ||
* [http://blog.kartena.se/local-projections-in-a-world-of-spherical-mercator/ Local projections in a world of spherical mercator] | * [http://blog.kartena.se/local-projections-in-a-world-of-spherical-mercator/ Local projections in a world of spherical mercator] | ||
* [http://mapproxy.org/docs/latest/ | * [http://mapproxy.org/docs/latest/configuration.html#id5 MapProxy grids configuration] | ||
* [http://mapproxy.org/docs/latest/ | * [http://mapproxy.org/docs/latest/mapproxy_util.html#grids mapproxy-util] | ||
* [http://msdn.microsoft.com/en-us/library/aa940990.aspx Understanding Scale and Resolution] | |||
* [http://wiki.openstreetmap.org/wiki/Slippy_map_tilenames Slippy map tilenames] | |||
* [https://getsatisfaction.com/opengeo/topics/how_do_i_interpret_the_openlayers_scale How do I interpret the OpenLayers scale?] | |||
Текущая версия от 13:42, 15 апреля 2013
по адресу http://gis-lab.info/qa/tile-matrix.html
Введение
Предположим, что вы ознакомились со спецификацией Tile Map Service и решили создать собственный TMS-сервис. Спецификация предполагает, что у вас уже есть готовый набор тайлов или перечень необходимых настроек, согласно которому эти тайлы будут создаваться (см. раздел URL, являющиеся скриптами). Наиболее распространенной является ситуация, когда автор TMS-сервиса не только создаёт прослойку между готовым набором тайлов и клиентским приложением, но и отвечает за подготовку самих тайлов. В этом случае разработчик должен хорошо разбираться в вопросах, связанных с конфигурированием тайловых сеток. Даже если в его приложении тайлы создаются по запросу, то есть "на лету", эти знания все равно крайне необходимы.
Параметры тайловой сетки
Проекция
Прежде всего важно определиться с проекцией, которая будет использоваться при отрисовке данных. Для этого необходимо ответить на вопрос для каких целей будут предназначены ваши тайлы. Если вы хотите просто отображать свою карту поверх подложек, предоставляемых такими сервисами как OpenStreetMap или Google Maps, то вы должны использовать такую же проекцию, что и указанные сервисы, а именно EPSG:3857. Если же вы преследуете какие-то иные цели, например, желаете вычислять расстояния, измерять площади объектов на карте или планируете создать карту Антарктиды, то в этом случае вам необходимо выбрать наиболее подходящую для этих задач проекцию.
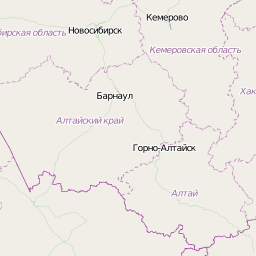
В качестве примера в данной статье мы будем конфигурировать тайловую сетку на территорию Алтайского края, поэтому для отрисовки данных будем использовать проекцию UTM зона 44 EPSG:32644, что в дальнейшем позволит нам осуществлять корректное измерение расстояний на полученной карте.
Охват
Следующий важный этап - это выбрать охват (ограничивающий прямоугольник), то есть ту область на которую будут генерироваться тайлы, вне ее тайлы не создаются. Параметры охвата Алтайского края получим на основе данных слоя административных границ набора Geosample. Для этого воспользуемся утилитой ogrinfo:
ogrinfo -sql "SELECT ST_Transform(the_geom, 32644) FROM admin WHERE name='Алтайский край'" PG:"host=gis-lab.info dbname=geosample user=guest password=guest" | grep Extent
В результате чего мы получим охват интересующей нас территории в единицах измерения системы координат проекции EPSG:32644 (minx, miny, maxx, maxy):
Extent: (287157.161574, 5613155.489664) - (920220.378205, 6045880.725611)
Масштабные уровни (разрешения)
После того, как мы определились с проекцией и охватом, необходимо разобраться с масштабными уровнями. Каждый масштабный уровень определяет разрешение с которым будет отрендерена карта на данном уровне, при этом количество таких уровней может быть произвольным. Величина разрешения, используемого на том или ином уровне также ничем не лимитирована. Разрешение показывает сколько единиц измерения координат исходных данных укладывается в одном пикселе отрендеренной карты. Таким образом в нашем случае (проекция UTM) единицы измерения разрешения - м/пиксел, в случае же работы с географическими системами координат это будут градус/пиксел.
Предположим, мы хотим предоставить доступ к нашим данным, отрендеренным с разрешениями R, равными 3000 и 1500 метров на пиксел. Посчитаем для этих разрешений размеры результирующей карты (w - ширина, h - высота):
w = (maxx - minx)/R = (920220-287157)/3000 = 211 (пикселов) h = (maxy - miny)/R = (6045880-5613155)/3000 = 144 (пикселов)
w = (maxx - minx)/R = (920220-287157)/1500 = 422 (пикселов) h = (maxy - miny)/R = (6045880-5613155)/1500 = 288 (пикселов)
Как уже было отмечено выше, разрешение -го масштабного уровня может быть произвольным, однако на практике наиболее распространённым является случай, когда разрешение -го уровня в 2 раза выше разрешения предыдущего :
Разрешение 0-го () масштабного уровня может устанавливаться произвольно, но опять же на практике широкое распространение получил следующий подход. Считается, что на нулевом уровне должно быть такое разрешение, которое бы позволило уместить карту целиком в один тайл. Чтобы его рассчитать, нам необходимо определиться с размерами тайла.
Размер тайла (ширина и высота) определяет объём информации, передаваемой одним тайлом. Очевидно, что чем больше геометрические размеры тайла, тем больший объём дискового пространства он занимает и тем дольше он будет передаваться клиенту. Чем меньше размер тайла, тем он быстрее может быть доставлен клиенту, но при этом возрастает количество запросов с серверу, что в конечном итоге приводит к еще более длительному процессу получения тайлов. Экспериментальным путём было установлено, что наиболее эффективный размер тайла - 256x256 пикселов.
Вернёмся к нашей задаче определения разрешения 0-го уровня. Определим ширину (W) и высоту (H) карты в единицах измерения данных:
W = maxx-minx = 920220-287157 = 633063 (м) H = maxy-miny = 6045880-5613155 = 432725 (м)
Тогда разрешение 0-го уровня можно вычислить так:
R0 = max(W,H)/256 = 633063/256 = 2472 (м/пиксел)
Можно записать общую формулу расчета разрешения z-го уровня карты размером WxH с размером тайла 256x256 с учётом того, что разрешение каждого последующего масштабного уровня в 2 раза выше предыдущего:
Положение начала отсчёта тайловой сетки
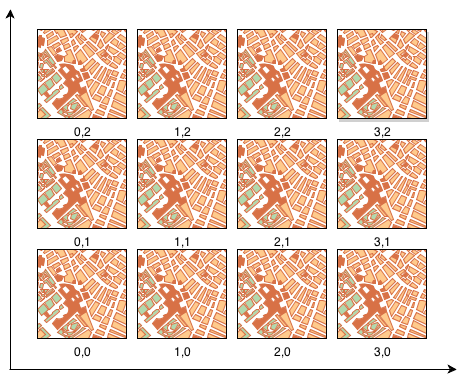
Начало отсчёта тайловой сетки, задаваемое в единицах измерения исходных данных, определяет индексы тайлов, по которым они будут доступны. Согласно спецификации TMS начало отсчёта тайловой сетки может располагаться вне охвата карты. В этом случае тайл (0,0) может и не существовать, однако это достаточно экзотический случай. Наиболее распространённым является случай, когда начало отсчёта тайловой сетки совпадает с координатами левого нижнего угла охвата карты (minx, miny):
Другой часто встречающийся случай (не согласующийся со спецификацией TMS) - это когда положение начала отсчета тайловой сетки помещается в левую верхнюю точку охвата карты (minx, maxy):
Данный подход используется, например, в OpenStreetMap:
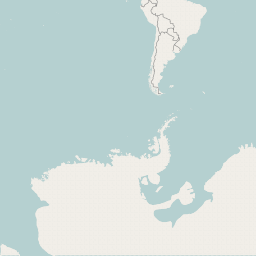
Как можно заметить на данном тайле представлена нижняя левая часть карты мира, но номер тайла при этом не (0,0), а (0,1).
Количество тайлов на различных масштабных уровнях
На основе вышесказанного можно легко оценить количество тайлов (x*y) на z-м масштабном уровне. Количество столбцов тайлов (x) определяется соотношением:
x = w/256 = W/(Rz*256)
Количество строк (y):
y = h/256 = H/(Rz*256)
Вычислим количество тайлов, например, на 7 масштабном уровне с учётом, что зависимость разрешения от номера уровня задана функцией, полученной в разделе #Масштабные уровни (разрешения):
R7 = max(W,H)/(256*2^z) = 633063/(256*2^7) = 19.32 x = 633063/(19.32*256) = 128 y = 432725/(19.32*256) = 88 x*y = 128*88 = 11264
Полученные значения x и y были округлены в большую сторону до целого.
Для автоматизации подсчёта количества тайлов на каждом масштабном уровне воспользуемся консольной утилитой, идущей в составе кэширующего прокси-сервера MapProxy. Для этого вначале составим описание тайловой сетки в специальном конфигурационном файле MapProxy mapproxy.yaml. После прочтения вышеизложенного материала данной статьи у вас должно появиться четкое понимание описываемых в следующей конфигурации параметров:
grids:
utmgrid:
srs: EPSG:32644
bbox_srs: EPSG:32644
tile_size: [256, 256]
origin: ll # low left
bbox: [287157.161574,5613155.489664,920220.378205,6045880.725611]
Запускаем утилиту:
mapproxy-util grids --grid utmgrid --mapproxy-conf mapproxy.yaml
Получаем результат:
Configuration:
bbox: [287157.161574, 5613155.489664, 920220.378205, 6045880.725611]
bbox_srs: 'EPSG:32644'
origin: 'll'
srs: 'EPSG:32644'
tile_size: [256, 256]
Levels: Resolutions, # x * y = total tiles
00: 2472.9031899648435, # 1 * 1 = 1
01: 1236.4515949824217, # 2 * 2 = 4
02: 618.2257974912109, # 4 * 3 = 12
03: 309.11289874560543, # 8 * 6 = 48
04: 154.55644937280272, # 16 * 11 = 176
05: 77.27822468640136, # 32 * 22 = 704
06: 38.63911234320068, # 64 * 44 = 2.816K
07: 19.31955617160034, # 128 * 88 = 11.264K
08: 9.65977808580017, # 256 * 175 = 44.800K
09: 4.829889042900085, # 512 * 350 = 179.200K
10: 2.4149445214500425, # 1024 * 700 = 716.800K
11: 1.2074722607250212, # 2048 * 1400 = 2.867M
12: 0.6037361303625106, # 4096 * 2800 = 11.469M
13: 0.3018680651812553, # 8192 * 5600 = 45.875M
14: 0.15093403259062765, # 16384 * 11200 = 183.501M
15: 0.07546701629531383, # 32768 * 22399 = 733.970M
16: 0.03773350814765691, # 65536 * 44797 = 2.936G
17: 0.018866754073828457, # 131072 * 89594 = 11.743G
18: 0.009433377036914228, # 262144 * 179187 = 46.973G
19: 0.004716688518457114, # 524288 * 358373 = 187.891G
Как можно заметить, уже на 11 масштабном уровне количество тайлов превысило отметку в 1 миллион, а на 16 в 1 миллиард.
Проведём оценку количества тайлов на различных масштабных уровнях сервиса OpenStreetMap. Для этого вновь воспользуемся утилитой из состава MapProxy и указав в качестве имени сетки специальное служебное значение GLOBAL_MERCATOR:
mapproxy-util grids --grid GLOBAL_MERCATOR --mapproxy-conf mapproxy.yaml
Результат:
Configuration:
bbox*: [-20037508.342789244, -20037508.342789244, 20037508.342789244, 20037508.342789244]
origin*: 'sw'
srs: 'EPSG:900913'
tile_size*: [256, 256]
Levels: Resolutions, # x * y = total tiles
00: 156543.03392804097, # 1 * 1 = 1
01: 78271.51696402048, # 2 * 2 = 4
02: 39135.75848201024, # 4 * 4 = 16
03: 19567.87924100512, # 8 * 8 = 64
04: 9783.93962050256, # 16 * 16 = 256
05: 4891.96981025128, # 32 * 32 = 1.024K
06: 2445.98490512564, # 64 * 64 = 4.096K
07: 1222.99245256282, # 128 * 128 = 16.384K
08: 611.49622628141, # 256 * 256 = 65.536K
09: 305.748113140705, # 512 * 512 = 262.144K
10: 152.8740565703525, # 1024 * 1024 = 1.049M
11: 76.43702828517625, # 2048 * 2048 = 4.194M
12: 38.21851414258813, # 4096 * 4096 = 16.777M
13: 19.109257071294063, # 8192 * 8192 = 67.109M
14: 9.554628535647032, # 16384 * 16384 = 268.435M
15: 4.777314267823516, # 32768 * 32768 = 1.074G
16: 2.388657133911758, # 65536 * 65536 = 4.295G
17: 1.194328566955879, # 131072 * 131072 = 17.180G
18: 0.5971642834779395, # 262144 * 262144 = 68.719G
19: 0.29858214173896974, # 524288 * 524288 = 274.878G
Так как в OpenStreetMap тайлы рендерятся только до 18 уровня, то получаем, что на последнем уровне количество тайлов достигает отметки 68 миллиардов.
Подробнее о разрешениях
Строго говоря выражение "карта на таком-то масштабном уровне отрендерена с таким-то разрешением" в общем случае имеет слабую связь с реальными размерами элементов изображения на местности из-за непостоянства размеров вносимого проекционными искажениями. Покажем это на примере игры на базе данных Google Maps, использующих проекцию Меркатора. Среди разбросанных полигонов найдите соответствующий Австралии и оцените как изменяется его форма в области полюсов и на своём законном месте (полигоны можно двигать, цель игры - разместить контуры стран по своим местам):
|url=http://gmaps-samples.googlecode.com/svn/trunk/poly/puzzledrag.html |width=1024 |height=640 |border=0
}}Изменение формы обусловлено выбранной проекцией - так в проекции Меркатора размеры элемента изображения карты не являются постоянными на местности. Линейные размеры увеличиваются от экватора к полюсам как обратный косинус широты (Проекция Меркатора). Таким образом, мы получаем, что пикселы даже в рамках одного тайла могут иметь различный размер:
В общем случаем линейные размеры пиксела - это функция от его географических координат (, ) и масштабного уровня:
В случае проекции Меркатора . С учётом этого выражение для вычисления разрешения принимает вид:
Получается, что в сервисах, использующих проекцию Меркатора разрешение в области 60 широты в 2 раза выше разрешения на экваторе (в одном пикселе отрендеренной карты укладывается меньше единиц измерения координат исходных данных) и соответствует действительности как раз на экваторе.
Тогда что-же мы подразумевали в предыдущих разделах данной статьи, говоря "разрешение z-го масштабного уровня"? Это ни что иное как некоторая абстрактная величина, имеющая размерность разрешения, которую удобно использовать для расчёта общего количества и координат тайлов. Если же мы хотим осуществлять измерения по нашей карте, то мы должны обязательно учитывать зависимость разрешения от географических координат. Выбрав в самом начале статьи проекцию UTM для рендеринга и заявив, что это "позволит нам осуществлять корректное измерение расстояний на полученной карте", мы обеспечили постоянство разрешения карты в пределах масштабного уровня, то есть независимость от географических координат: .
Понятие экранного масштаба карты
Экранный масштаб карты (S) показывает сколько единиц измерения на местности укладывается в единицу измерения карты на экране монитора и равен произведению разрешения карты на разрешение экрана (dots per inch, DPI) и на количество единиц карты в одной единице измерения разрешения экрана (inches per map unit, IPMU):
Как было показано выше - разные области карты могут иметь различное разрешение, а, следовательно, и масштаб.