Вычисление площади полигона на сфере и на эллипсоиде: различия между версиями
ErnieBoyd (обсуждение | вклад) м (→Ссылки) |
ErnieBoyd (обсуждение | вклад) |
||
| (не показаны 154 промежуточные версии 3 участников) | |||
| Строка 1: | Строка 1: | ||
{{Статья| | {{Статья|Опубликована|polygon-area-sphere-ellipsoid}} | ||
{{Аннотация| | {{Аннотация|Рассматривается известный способ вычисления площади сферического полигона по сферическому избытку. Предлагается расширение этого подхода на поверхность эллипсоида. Приводится пример программной реализации на языке Питон.}} | ||
== Общие положения == | == Общие положения == | ||
| Строка 17: | Строка 17: | ||
В общем случае определение площади многоугольника на искривлённой поверхности — нетривиальная задача. Нужно интегрировать по поверхности с пределами, заданными неявно. К счастью, математика может предложить обходные пути решения задачи. | В общем случае определение площади многоугольника на искривлённой поверхности — нетривиальная задача. Нужно интегрировать по поверхности с пределами, заданными неявно. К счастью, математика может предложить обходные пути решения задачи. | ||
[[Image:Vertex-angles.png|frame|c|left|Углы при вершине полигона]] | |||
<math>\begin{ | Представим себе точку, движущуюся вдоль контура полигона. Вершины являются точками поворота. Внутренний угол при вершине ''θ'' равен разности азимутов направлений ''α'' в предыдущую и следующую вершины, а поворот есть угол ''τ'', смежный внутреннему: | ||
\theta_i & = | |||
\tau_i & = | : <math>\begin{align} | ||
\end{ | \theta_i & = \alpha_{i, i-1} - \alpha_{i, i+1} \\ | ||
\tau_i & = \pi - \theta_i | |||
\end{align}</math> | |||
На евклидовой плоскости, обойдя любой замкнутый контур без самопересечений, точка совершает поворот ровно на одну окружность — 360°, или 2''π'' радиан. В случае многоугольника этот поворот складывается из суммы поворотов в вершинах. | На евклидовой плоскости, обойдя любой замкнутый контур без самопересечений, точка совершает поворот ровно на одну окружность — 360°, или 2''π'' радиан. В случае многоугольника этот поворот складывается из суммы поворотов в вершинах. | ||
| Строка 34: | Строка 36: | ||
В общем случае кривизна поверхности меняется в каждой точке, но не на сфере! Кривизна сферы постоянна, и площадь замкнутой фигуры однозначно соотносится с полным поворотом контура. | В общем случае кривизна поверхности меняется в каждой точке, но не на сфере! Кривизна сферы постоянна, и площадь замкнутой фигуры однозначно соотносится с полным поворотом контура. | ||
Отличие полного поворота от 2''π'' радиан называется сферическим избытком ''ε'', который пропорционален площади полигона ''S'': | Отличие полного поворота от 2''π'' радиан называется сферическим избытком или эксцессом ''ε'', который пропорционален площади полигона ''S'': | ||
<math>\begin{ | : <math>\begin{align} | ||
\varepsilon & = | \varepsilon & = 2 \pi - \displaystyle \sum_{i=1}^n \tau_i \\ | ||
S & = | S & = \varepsilon R^2 | ||
\end{ | \end{align}</math> | ||
где ''R'' — радиус сферы. | где ''R'' — радиус сферы. | ||
| Строка 54: | Строка 56: | ||
=== Радиус сферы === | === Радиус сферы === | ||
В геодезической и картографической практике в качестве модели Земли принимают эллипсоид вращения, характеризуемый величинами экваториального радиуса ''a'' и сжатия ''f''. Соответствующая сфера должна иметь такую же площадь, как и принимаемый за основу эллипсоид. Такая сфера называется эквивалентной (''authalic sphaera'' по латыни). | |||
Ниже мы приведём формулы вычисления радиуса эквивалентной сферы по параметрам эллипсоида. Пока же поближе посмотрим на пару-тройку популярных программных пакетов. | |||
'''MapInfo''' вычисляет площади на сфере по умолчанию. Несложные эксперименты («реверс-инжиниринг») показывает, что радиус сферы не зависит от того, на каком эллипсоиде построена координатная система обрабатываемых данных, — он всегда равен 6370997 метров ровно. Анализ используемых земных эллипсоидов показывает, что это соответствует радиусу эквивалентной сферы эллипсоида Кларка 1866 года, определяемого величинами экаториального радиуса ''a'' = 6378206.4 м и полярного радиуса ''b'' = 6356583.8 м; точное значение радиуса ''R<sub>auth</sub>'' = 6370997.2406 м, округлённое до метра — 6370997 м. | |||
Выбор именно этого радиуса не случаен: эллипсоид Кларка 1866 пока ещё широко используется в странах Северной Америки в картографических и кадастровых целях. | |||
В большинстве своём программы GIS не вычисляют площадей на сфере. Тем не менее, в картографических целях '''ArcGIS''' включает два эллипсоида с характерными названиями: <tt>“Authalic sphere (ARCINFO)”</tt> (код <tt>“SPHEROID["Sphere_ARC_INFO",6370997,0]”</tt>) и более новый <tt>“Authalic sphere”</tt> (код <tt>“SPHEROID["Sphere",6371000,0]”</tt>). | |||
В пакете '''PROJ.4''' также имеется эллипсоид <tt>“sphere”</tt>: параметры <tt>“a=6370997.0”</tt>, <tt>“b=6370997.0”</tt>, описание <tt>“Normal Sphere (r=6370997)”</tt>. | |||
=== Площадь малого полигона === | |||
Если полигон настолько мал, что сферический избыток сравним с погрешностью его вычисления, можно перейти к вычислениям площади на плоскости. | |||
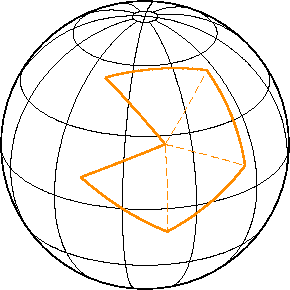
Для промежуточной по размерам зоны имеется следующий вариант решения проблемы. Полигон разбивается на сферические треугольники, как показано на рисунке пунктирными линиями. Решаются обратные задачи для каждой линии, из чего находятся длины сторон ''a'', ''b'', ''c'' и внутренние углы ''A'', ''B'', ''C'' каждого треугольника. После этого эксцессы ''ε<sub>j</sub>'' треугольников вычисляются, например, по первой формуле Каньоли: | |||
: <math>\sin \frac{\varepsilon}{2} = \frac{\sin \frac{a}{2} \sin \frac{b}{2}}{\cos \frac{c}{2}} \sin C</math> | |||
В итоге находится суммарный эксцесс ''ε'' = ∑''ε<sub>j</sub>'' и вычисляется площадь ''S''. | |||
В учебниках сферической тригонометрии можно найти и другие формулы вычисления сферического избытка в треугольнике. | |||
== Площадь полигона на эллипсоиде == | |||
=== Параметры эллипсоида === | |||
Обычно эллипсоид задаётся такими параметрами, как экваториальный радиус ''a'' и сжатие ''f''. Часто в качестве второго параметра приводят полярный радиус ''b''. Эти величины связаны простыми соотношениями: | |||
: <math>b = a (1 - f) \qquad f = 1 - \dfrac{b}{a}</math> | |||
Из основных параметров выводятся другие: полярный радиус кривизны ''c'', эксцентриситет ''e'', второй эксентриситет ''e′'': | |||
: <math>c = \frac{a}{1 - f} \qquad e^2 = f (2 - f) \qquad e'^2 = \frac{e^2}{1 - e^2}</math> | |||
=== Классический способ === | |||
Можно получать площади интегрированием по поверхности. Это сложно, поскольку пределы интегрирования в полигоне заданы неявно, но вполне реализуемо численными методами. | |||
Однако можно воспользоваться тем фактом, что средний по азимутам радиус кривизны поверхности эллипсоида является медленно меняющейся функцией широты: | |||
: <math>R = \frac{c}{1 + e'^2 \cos^2 \varphi}</math> | |||
В классическом способе для данной территории поверхность эллипсоида представляется сферой с радиусом, равным радиусу кривизны ''R'' на средней широте этой территории. Если территория имеет значительное простирание по широте, придётся её разбивать на более мелкие фигуры. Таким образом, мы вновь обращаемся к технике работы с малыми полигонами, описанной чуть выше. | |||
Классический способ издавна использовался при обработке измерений в геодезических сетях. Геодезистам не приходилось искуственно разбивать полигоны на треугольники, они уже были разбиты: в вершинах находились геодезические пункты, углы и/или длины сторон в каждом треугольнике измерялись. Отличалась только цель вычисления сферического избытка: он определялся не для установления площади, а для нахождения теоретической суммы углов в треугольниках. | |||
Характерные размеры треугольников определялись дальностью видимости между ''сигналами'' — вышками, установленными над центрами, — и составляли первые десятки километров, т.е. десятые доли процента от радиуса Земли. | |||
При обработке вычислялся общий радиус кривизны по средней широте территории работ. Этого было достаточно для нахождения сферического избытка. Однако для нахождения площадей точнее будет вычислять радиус кривизны индивидуально для каждого треугольника по широте его центра. | |||
Для огромной территории, заданной контуром без готового разбиения на достаточно мелкие фигуры, применение классического метода затруднительно. | |||
=== Эквивалентное отображение === | |||
Речь идёт об отображении поверхности эллипсоида на сферу. В математической картографии это распространённый подход, поскольку математика на сфере намного проще, чем на эллипсоиде. В данном случае необходимо совершить отображение, при котором сохраняются площади объектов — эквивалентное отображение. Площадь эквивалентной сферы равна площади поверхности эллипсоида. Приведём пару представлений радиуса этой сферы ''R<sub>auth</sub>'': | |||
: <math>R_{auth} = \sqrt{\frac{a^2}{2} + \frac{b^2}{2} \frac{\operatorname{Arth\,} e}{e}} = b \sqrt{1 + \frac{2}{3} e^2 + \frac{3}{5} e^4 + \frac{4}{7} e^6 + \cdots}</math> | |||
При эквивалентном отображении долгота на эллипсоиде ''λ'' равна долготе на эквивалентной сфере, а геодезической широте на эллипсоиде ''φ'' соответствует так называемая эквивалентная широта на сфере ''β'': | |||
: <math>\begin{align} | |||
\beta = \varphi & - \left( \frac{1}{3} e^2 + \frac{31}{180} e^4 + \frac{59}{560} e^6 + \cdots \right) \sin 2 \varphi + \left( \frac{17}{360} e^4 + \frac{61}{1260} e^6 + \cdots \right) \sin 4 \varphi - \\ | |||
& - \left( \frac{383}{45360} e^6 + \cdots \right) \sin 6 \varphi + \cdots | |||
\end{align}</math> | |||
Ряд такого вида называется тригонометрическим. | |||
=== Алгоритм вычисления площади === | |||
Пусть ''n''-угольник задан координатами вершин ''φ<sub>i</sub>'', ''λ<sub>i</sub>'', где ''φ<sub>i</sub>'' — широта ''i''-ой вершины, ''λ<sub>i</sub>'' — долгота, ''i'' = 1, … , ''n''. | |||
Алгоритм вычисления площади на эллипсоиде с использованием эквивалентного отображения совпадает с алгоритмом для сферы, только в начале вставим переход от геодезических широт к эквивалентным. | |||
# Для каждой вершины по геодезической широте ''φ<sub>i</sub>'' вычисляем эквивалентную широту ''β<sub>i</sub>''. | |||
# Для каждой стороны из решения [http://gis-lab.info/qa/sphere-geodesic-invert-problem.html обратной геодезической задачи] для её конечных вершин находим прямые и обратные азимуты ''α''<sub>''i'', ''i''+1</sub> и ''α''<sub>''i''+1, ''i''</sub>. | |||
# Для каждой вершины по азимутам ''α''<sub>''i'', ''i''−1</sub> в предыдущую и ''α''<sub>''i'', ''i''+1</sub> в последующую вершины находим поворот ''τ<sub>i</sub>'' и добавляем его к полному повороту ''τ''. | |||
# Вычисляем сферический избыток ''ε''. | |||
# Вычисляем площадь полигона ''S''. | |||
=== Замечания === | |||
Важно помнить, что геодезическая линия на эллипсоиде не отображается в дугу большой окружности на сфере. Правда, отличие становится заметным лишь при длинах сторон, сравнимых с размерами Земли. Так, при самом неудачном положении линии длиной 4 тысячи километров «провисание» в середине приближается к пяти километрам. Для линий, вытянутых вдоль меридианов, «провисание» отсутствует. | |||
В каждую длинную сторону, не являющуюся отрезком меридиана, следует вставлять дополнительные вершины. Для этого надо решать одну обратную и много прямых геодезических задач, только не на сфере, а на эллипсоиде, используя алгоритмы сфероидической геодезии. Только после этого можно пересчитывать геодезические широты промежуточных узлов в широты эквивалентные. Чем короче полученные отрезки, тем меньше расхождение между дугой большой окружности на эквивалентной сфере и отображением геодезической линии. Можно сделать процедуру вставки итеративной, т.е. добавлять точки до сходимости площади в пределах заданной точности. | |||
К счастью, береговые линии и границы государств обычно образованы сравнительно короткими отрезками полилиний. А длинные границы полярных владений вытянуты вдоль меридианов, которые являются геодезическими линиями. | |||
Отрезки параллелей, напротив, геодезическими линиями не являются. Вдоль геодезической линии поворот по определению равен нулю. Параллель же является кривой линией на поверхности. Замечательно, что кривизна её постоянна, что даёт простую зависимость поворота вдоль отрезка параллели от широты и разности долгот: | |||
: <math>\Delta \tau = \left( \lambda_1 - \lambda_2 \right) \sin \beta</math> | |||
Вместе с тем фактом, что азимуты начальных и конечных направлений параллелей всегда равны 90° либо 270°, это позволяет легко вычислять повороты контуров, составленных частично отрезками геодезических, а частично отрезками параллелей. В частности, если территория является сфероидической трапецией, ограниченной отрезками двух меридианов и двух параллелей, получаем следующую формулу вычисления площади: | |||
: <math>S = R_{auth}^2 (\lambda_2 - \lambda_1) (\sin \beta_2 - \sin \beta_1)</math> | |||
где ''λ''₁ и ''λ''₂ — долготы западной и восточной границ, ''β''₁ и ''β''₂ — эквивалентные широты южной и северной границ. | |||
== Программная реализация == | |||
Создадим скрипт на языке Питон, предназначенный для вычисления площади полигона на эллипсоиде. Используем эквивалентное отображение эллипсоида на сферу, на которой и будет вычисляться площадь. | |||
Эллипсоид зададим большой полуосью ''a'' и сжатием ''f''. Скрипт должен работать и для сферы; в этом случае в качестве ''a'' задаётся радиус сферы, а ''f'' приравнивается нулю. | |||
Данные должны будут читаться из файла. | |||
=== Вспомогательные функции === | |||
Создадим несколько функций. Во-первых, нам понадобится реализация степенного ряда: | |||
<syntaxhighlight lang="python"> | |||
# степенной ряд | |||
def powSeries(x, p1, p2, p3): | |||
return (p1 + (p2 + p3 * x) * x) * x | |||
</syntaxhighlight> | |||
Она облегчит нам вычисление радиуса эквивалентной сферы и коэффициентов тригонометрического ряда: | |||
<syntaxhighlight lang="python"> | |||
# инициализация эквивалентной сферы | |||
def init(a, f): | |||
b = a * (1. - f) | |||
e2 = f * (2. - f) | |||
R_auth = b * math.sqrt(1. + powSeries(e2, 2./3., 3./5., 4./7.)) | |||
to_auth_2 = powSeries(e2, -1./3., -31./180., -59./560.) | |||
to_auth_4 = powSeries(e2, 0., 17./360., 61./1260.) | |||
to_auth_6 = powSeries(e2, 0., 0., -383./45360.) | |||
return (R_auth, to_auth_2, to_auth_4, to_auth_6) | |||
</syntaxhighlight> | |||
Наконец, подготовим реализацию тригонометрического ряда: | |||
<syntaxhighlight lang="python"> | |||
# тригонометрический ряд | |||
def trigSeries(x, t2, t4, t6): | |||
return x + t2 * math.sin(2. * x) + t4 * math.sin(4. * x) + t6 * math.sin(6. * x) | |||
</syntaxhighlight> | |||
Эти функции можно найти в архиве [[Медиа:Auth.zip|Auth.zip]] в файле '''auth.py'''. Также в архиве находится файл '''sph.py''', необходимый для решения обратной геодезической задачи на сфере. | |||
=== Программа === | |||
Напишем программу вычисления площади полигона. | |||
В примере задаются параметры эллипсоида WGS 84, по которым вычисляются радиус эквивалентной сферы и коэффициенты тригонометрического ряда для пересчёта геодезической широты в эквивалентную. | |||
Далее программа читает из файла данных вершины полигона, представленные парами геодезических координат ''λ'', ''φ'', и по приведённому выше алгоритму вычисляет площадь. | |||
<syntaxhighlight lang="python"> | |||
# -*- coding: utf-8 -*- | |||
# вычисление площади сфероидического полигона | |||
from sys import argv | |||
import math | |||
import sph | |||
import auth | |||
script, fname = argv | |||
a, f = 6378.137, 1./298.257223563 # большая полуось и сжатие | |||
# инициализировать эквивалентную сферу | |||
r_auth, to_auth_2, to_auth_4, to_auth_6 = auth.init(a, f) | |||
fp = open(fname, 'r') | |||
tau = 0. | |||
i = 1 | |||
for line in fp: | |||
# прочитать долготу и широту | |||
lon, lat = map(float, line.split(" ")) | |||
lon = math.radians(lon) | |||
lat = math.radians(lat) | |||
# вычислить эквивалентную широту | |||
lat = auth.trigSeries(lat, to_auth_2, to_auth_4, to_auth_6) | |||
if i > 1: | |||
# вычислить прямой азимут Qi - Qi+1 | |||
dist, azi1 = sph.inverse(lat1, lon1, lat, lon) | |||
if i == 2: | |||
# запомнить азимут Q1 - Q2 | |||
azi0 = azi1 | |||
else: | |||
# вычислить поворот в i-й вершине | |||
tau_i = 0.5 - (azi2 - azi1) / 2. / math.pi | |||
# нормализовать величину поворота | |||
tau_i = tau_i - math.floor(tau_i + 0.5) | |||
# добавить поворот к сумме поворотов | |||
tau = tau + tau_i | |||
# вычислить обратный азимут Qi+1 - Qi | |||
dist, azi2 = sph.inverse(lat, lon, lat1, lon1) | |||
lon1, lat1 = lon, lat | |||
i = i + 1 | |||
fp.close() | |||
# вычислить поворот в 1-й вершине | |||
tau_i = 0.5 - (azi2 - azi0) / 2. / math.pi | |||
# нормализовать величину поворота | |||
tau_i = tau_i - math.floor(tau_i + 0.5) | |||
# добавить поворот к сумме поворотов | |||
tau = tau + tau_i | |||
# вычислить площадь | |||
area = 2. * math.pi * (1. - math.fabs(tau)) * r_auth ** 2 | |||
print "%g" % area | |||
</syntaxhighlight> | |||
Код программы находится в архиве [[Медиа:Auth.zip|Auth.zip]] в файле '''area.py'''. | |||
Чтобы скрипт был предельно прост, не выполняются некоторые необходимые проверки. Поэтому к данным предъявляются такие требования: | |||
* последняя точка должна совпадать с первой; | |||
* точки не должны дублироваться. | |||
По координатам, использованным при построении рисунка, подготовим файл данных '''polygon.dat''': | |||
<pre> | |||
18 -10.812317 | |||
-18 10.812317 | |||
18 26.565051 | |||
-18 52.622632 | |||
54 52.622632 | |||
54 10.812317 | |||
18 -10.812317 | |||
</pre> | |||
Выполним скрипт в консоли: | |||
<syntaxhighlight lang="bash"> | |||
$ python area.py polygon.dat | |||
</syntaxhighlight> | |||
Вывод программы: | |||
<pre>3.39532e+07</pre> | |||
Поскольку большая полуось задавалась в километрах, результат получен в квадратных километрах. | |||
Посмотрев на рисунок, легко заметить, что длины сторон нашего полигона сравнимы с радиусом сферы, и упомянутый выше эффект «провисания» линий может повлиять на точность вычисления площади. | |||
== Ссылки == | == Ссылки == | ||
* [http://gis-lab.info/qa/sphere-geodesic-invert-problem.html Задачи на сфере: обратная геодезическая задача] | * [http://gis-lab.info/qa/sphere-geodesic-invert-problem.html Задачи на сфере: обратная геодезическая задача] | ||
* [http://en.wikipedia.org/wiki/Earth_radius Earth radius] | * [http://en.wikipedia.org/wiki/Earth_radius Earth radius] | ||
* [http://www.pm298.ru/sferich.php Краткий справочник по сферической тригонометрии] | |||
* [http://docs.lib.noaa.gov/rescue/cgs_specpubs/QB275U35no671921.pdf Latitude Developments Connected with Geodesy and Cartography with Tables including a Table for Lambert equal-area Meridional Projection] | |||
* [http://gis-lab.info/docs/books/sphere-trigonometry/sphere-trigonometry.rar Степанов Н. Н. Сферическая тригонометрия] | |||
Текущая версия от 09:54, 1 июля 2014
по адресу http://gis-lab.info/qa/polygon-area-sphere-ellipsoid.html
Рассматривается известный способ вычисления площади сферического полигона по сферическому избытку. Предлагается расширение этого подхода на поверхность эллипсоида. Приводится пример программной реализации на языке Питон.
Общие положения
Определим полигон как простой многоугольник — участок поверхности, ограниченный замкнутой полилинией без самопересечений.
Полилиния в свою очередь — ломаная, образованная отрезками геодезических линий.
Геодезическая линия на плоскости — это прямая; геодезическая линия на сфере — дуга большой окружности.
Полный поворот контура
В общем случае определение площади многоугольника на искривлённой поверхности — нетривиальная задача. Нужно интегрировать по поверхности с пределами, заданными неявно. К счастью, математика может предложить обходные пути решения задачи.
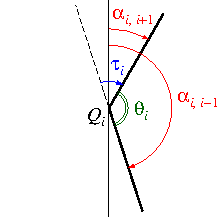
Представим себе точку, движущуюся вдоль контура полигона. Вершины являются точками поворота. Внутренний угол при вершине θ равен разности азимутов направлений α в предыдущую и следующую вершины, а поворот есть угол τ, смежный внутреннему:
На евклидовой плоскости, обойдя любой замкнутый контур без самопересечений, точка совершает поворот ровно на одну окружность — 360°, или 2π радиан. В случае многоугольника этот поворот складывается из суммы поворотов в вершинах.
На поверхности с ненулевой гауссовой кривизной общий поворот отличается от 2π на величину избытка или недостатка, пропорционального кривизне поверхности и площади фигуры.
Площадь полигона на сфере
Сферический избыток
В общем случае кривизна поверхности меняется в каждой точке, но не на сфере! Кривизна сферы постоянна, и площадь замкнутой фигуры однозначно соотносится с полным поворотом контура.
Отличие полного поворота от 2π радиан называется сферическим избытком или эксцессом ε, который пропорционален площади полигона S:
где R — радиус сферы.
Алгоритм вычисления площади
Пусть n-угольник задан координатами вершин φi, λi, где φi — широта i-ой вершины, λi — долгота, i = 1, … , n.
- Для каждой стороны из решения обратной геодезической задачи для её конечных вершин находим прямые и обратные азимуты αi, i+1 и αi+1, i.
- Для каждой вершины по азимутам αi, i−1 в предыдущую и αi, i+1 в последующую вершины находим поворот τi и добавляем его к полному повороту τ.
- Вычисляем сферический избыток ε.
- Вычисляем площадь полигона S.
Радиус сферы
В геодезической и картографической практике в качестве модели Земли принимают эллипсоид вращения, характеризуемый величинами экваториального радиуса a и сжатия f. Соответствующая сфера должна иметь такую же площадь, как и принимаемый за основу эллипсоид. Такая сфера называется эквивалентной (authalic sphaera по латыни).
Ниже мы приведём формулы вычисления радиуса эквивалентной сферы по параметрам эллипсоида. Пока же поближе посмотрим на пару-тройку популярных программных пакетов.
MapInfo вычисляет площади на сфере по умолчанию. Несложные эксперименты («реверс-инжиниринг») показывает, что радиус сферы не зависит от того, на каком эллипсоиде построена координатная система обрабатываемых данных, — он всегда равен 6370997 метров ровно. Анализ используемых земных эллипсоидов показывает, что это соответствует радиусу эквивалентной сферы эллипсоида Кларка 1866 года, определяемого величинами экаториального радиуса a = 6378206.4 м и полярного радиуса b = 6356583.8 м; точное значение радиуса Rauth = 6370997.2406 м, округлённое до метра — 6370997 м.
Выбор именно этого радиуса не случаен: эллипсоид Кларка 1866 пока ещё широко используется в странах Северной Америки в картографических и кадастровых целях.
В большинстве своём программы GIS не вычисляют площадей на сфере. Тем не менее, в картографических целях ArcGIS включает два эллипсоида с характерными названиями: “Authalic sphere (ARCINFO)” (код “SPHEROID["Sphere_ARC_INFO",6370997,0]”) и более новый “Authalic sphere” (код “SPHEROID["Sphere",6371000,0]”).
В пакете PROJ.4 также имеется эллипсоид “sphere”: параметры “a=6370997.0”, “b=6370997.0”, описание “Normal Sphere (r=6370997)”.
Площадь малого полигона
Если полигон настолько мал, что сферический избыток сравним с погрешностью его вычисления, можно перейти к вычислениям площади на плоскости.
Для промежуточной по размерам зоны имеется следующий вариант решения проблемы. Полигон разбивается на сферические треугольники, как показано на рисунке пунктирными линиями. Решаются обратные задачи для каждой линии, из чего находятся длины сторон a, b, c и внутренние углы A, B, C каждого треугольника. После этого эксцессы εj треугольников вычисляются, например, по первой формуле Каньоли:
В итоге находится суммарный эксцесс ε = ∑εj и вычисляется площадь S.
В учебниках сферической тригонометрии можно найти и другие формулы вычисления сферического избытка в треугольнике.
Площадь полигона на эллипсоиде
Параметры эллипсоида
Обычно эллипсоид задаётся такими параметрами, как экваториальный радиус a и сжатие f. Часто в качестве второго параметра приводят полярный радиус b. Эти величины связаны простыми соотношениями:
Из основных параметров выводятся другие: полярный радиус кривизны c, эксцентриситет e, второй эксентриситет e′:
Классический способ
Можно получать площади интегрированием по поверхности. Это сложно, поскольку пределы интегрирования в полигоне заданы неявно, но вполне реализуемо численными методами.
Однако можно воспользоваться тем фактом, что средний по азимутам радиус кривизны поверхности эллипсоида является медленно меняющейся функцией широты:
В классическом способе для данной территории поверхность эллипсоида представляется сферой с радиусом, равным радиусу кривизны R на средней широте этой территории. Если территория имеет значительное простирание по широте, придётся её разбивать на более мелкие фигуры. Таким образом, мы вновь обращаемся к технике работы с малыми полигонами, описанной чуть выше.
Классический способ издавна использовался при обработке измерений в геодезических сетях. Геодезистам не приходилось искуственно разбивать полигоны на треугольники, они уже были разбиты: в вершинах находились геодезические пункты, углы и/или длины сторон в каждом треугольнике измерялись. Отличалась только цель вычисления сферического избытка: он определялся не для установления площади, а для нахождения теоретической суммы углов в треугольниках.
Характерные размеры треугольников определялись дальностью видимости между сигналами — вышками, установленными над центрами, — и составляли первые десятки километров, т.е. десятые доли процента от радиуса Земли.
При обработке вычислялся общий радиус кривизны по средней широте территории работ. Этого было достаточно для нахождения сферического избытка. Однако для нахождения площадей точнее будет вычислять радиус кривизны индивидуально для каждого треугольника по широте его центра.
Для огромной территории, заданной контуром без готового разбиения на достаточно мелкие фигуры, применение классического метода затруднительно.
Эквивалентное отображение
Речь идёт об отображении поверхности эллипсоида на сферу. В математической картографии это распространённый подход, поскольку математика на сфере намного проще, чем на эллипсоиде. В данном случае необходимо совершить отображение, при котором сохраняются площади объектов — эквивалентное отображение. Площадь эквивалентной сферы равна площади поверхности эллипсоида. Приведём пару представлений радиуса этой сферы Rauth:
При эквивалентном отображении долгота на эллипсоиде λ равна долготе на эквивалентной сфере, а геодезической широте на эллипсоиде φ соответствует так называемая эквивалентная широта на сфере β:
Ряд такого вида называется тригонометрическим.
Алгоритм вычисления площади
Пусть n-угольник задан координатами вершин φi, λi, где φi — широта i-ой вершины, λi — долгота, i = 1, … , n.
Алгоритм вычисления площади на эллипсоиде с использованием эквивалентного отображения совпадает с алгоритмом для сферы, только в начале вставим переход от геодезических широт к эквивалентным.
- Для каждой вершины по геодезической широте φi вычисляем эквивалентную широту βi.
- Для каждой стороны из решения обратной геодезической задачи для её конечных вершин находим прямые и обратные азимуты αi, i+1 и αi+1, i.
- Для каждой вершины по азимутам αi, i−1 в предыдущую и αi, i+1 в последующую вершины находим поворот τi и добавляем его к полному повороту τ.
- Вычисляем сферический избыток ε.
- Вычисляем площадь полигона S.
Замечания
Важно помнить, что геодезическая линия на эллипсоиде не отображается в дугу большой окружности на сфере. Правда, отличие становится заметным лишь при длинах сторон, сравнимых с размерами Земли. Так, при самом неудачном положении линии длиной 4 тысячи километров «провисание» в середине приближается к пяти километрам. Для линий, вытянутых вдоль меридианов, «провисание» отсутствует.
В каждую длинную сторону, не являющуюся отрезком меридиана, следует вставлять дополнительные вершины. Для этого надо решать одну обратную и много прямых геодезических задач, только не на сфере, а на эллипсоиде, используя алгоритмы сфероидической геодезии. Только после этого можно пересчитывать геодезические широты промежуточных узлов в широты эквивалентные. Чем короче полученные отрезки, тем меньше расхождение между дугой большой окружности на эквивалентной сфере и отображением геодезической линии. Можно сделать процедуру вставки итеративной, т.е. добавлять точки до сходимости площади в пределах заданной точности.
К счастью, береговые линии и границы государств обычно образованы сравнительно короткими отрезками полилиний. А длинные границы полярных владений вытянуты вдоль меридианов, которые являются геодезическими линиями.
Отрезки параллелей, напротив, геодезическими линиями не являются. Вдоль геодезической линии поворот по определению равен нулю. Параллель же является кривой линией на поверхности. Замечательно, что кривизна её постоянна, что даёт простую зависимость поворота вдоль отрезка параллели от широты и разности долгот:
Вместе с тем фактом, что азимуты начальных и конечных направлений параллелей всегда равны 90° либо 270°, это позволяет легко вычислять повороты контуров, составленных частично отрезками геодезических, а частично отрезками параллелей. В частности, если территория является сфероидической трапецией, ограниченной отрезками двух меридианов и двух параллелей, получаем следующую формулу вычисления площади:
где λ₁ и λ₂ — долготы западной и восточной границ, β₁ и β₂ — эквивалентные широты южной и северной границ.
Программная реализация
Создадим скрипт на языке Питон, предназначенный для вычисления площади полигона на эллипсоиде. Используем эквивалентное отображение эллипсоида на сферу, на которой и будет вычисляться площадь.
Эллипсоид зададим большой полуосью a и сжатием f. Скрипт должен работать и для сферы; в этом случае в качестве a задаётся радиус сферы, а f приравнивается нулю.
Данные должны будут читаться из файла.
Вспомогательные функции
Создадим несколько функций. Во-первых, нам понадобится реализация степенного ряда:
# степенной ряд
def powSeries(x, p1, p2, p3):
return (p1 + (p2 + p3 * x) * x) * x
Она облегчит нам вычисление радиуса эквивалентной сферы и коэффициентов тригонометрического ряда:
# инициализация эквивалентной сферы
def init(a, f):
b = a * (1. - f)
e2 = f * (2. - f)
R_auth = b * math.sqrt(1. + powSeries(e2, 2./3., 3./5., 4./7.))
to_auth_2 = powSeries(e2, -1./3., -31./180., -59./560.)
to_auth_4 = powSeries(e2, 0., 17./360., 61./1260.)
to_auth_6 = powSeries(e2, 0., 0., -383./45360.)
return (R_auth, to_auth_2, to_auth_4, to_auth_6)
Наконец, подготовим реализацию тригонометрического ряда:
# тригонометрический ряд
def trigSeries(x, t2, t4, t6):
return x + t2 * math.sin(2. * x) + t4 * math.sin(4. * x) + t6 * math.sin(6. * x)
Эти функции можно найти в архиве Auth.zip в файле auth.py. Также в архиве находится файл sph.py, необходимый для решения обратной геодезической задачи на сфере.
Программа
Напишем программу вычисления площади полигона.
В примере задаются параметры эллипсоида WGS 84, по которым вычисляются радиус эквивалентной сферы и коэффициенты тригонометрического ряда для пересчёта геодезической широты в эквивалентную.
Далее программа читает из файла данных вершины полигона, представленные парами геодезических координат λ, φ, и по приведённому выше алгоритму вычисляет площадь.
# -*- coding: utf-8 -*-
# вычисление площади сфероидического полигона
from sys import argv
import math
import sph
import auth
script, fname = argv
a, f = 6378.137, 1./298.257223563 # большая полуось и сжатие
# инициализировать эквивалентную сферу
r_auth, to_auth_2, to_auth_4, to_auth_6 = auth.init(a, f)
fp = open(fname, 'r')
tau = 0.
i = 1
for line in fp:
# прочитать долготу и широту
lon, lat = map(float, line.split(" "))
lon = math.radians(lon)
lat = math.radians(lat)
# вычислить эквивалентную широту
lat = auth.trigSeries(lat, to_auth_2, to_auth_4, to_auth_6)
if i > 1:
# вычислить прямой азимут Qi - Qi+1
dist, azi1 = sph.inverse(lat1, lon1, lat, lon)
if i == 2:
# запомнить азимут Q1 - Q2
azi0 = azi1
else:
# вычислить поворот в i-й вершине
tau_i = 0.5 - (azi2 - azi1) / 2. / math.pi
# нормализовать величину поворота
tau_i = tau_i - math.floor(tau_i + 0.5)
# добавить поворот к сумме поворотов
tau = tau + tau_i
# вычислить обратный азимут Qi+1 - Qi
dist, azi2 = sph.inverse(lat, lon, lat1, lon1)
lon1, lat1 = lon, lat
i = i + 1
fp.close()
# вычислить поворот в 1-й вершине
tau_i = 0.5 - (azi2 - azi0) / 2. / math.pi
# нормализовать величину поворота
tau_i = tau_i - math.floor(tau_i + 0.5)
# добавить поворот к сумме поворотов
tau = tau + tau_i
# вычислить площадь
area = 2. * math.pi * (1. - math.fabs(tau)) * r_auth ** 2
print "%g" % area
Код программы находится в архиве Auth.zip в файле area.py.
Чтобы скрипт был предельно прост, не выполняются некоторые необходимые проверки. Поэтому к данным предъявляются такие требования:
- последняя точка должна совпадать с первой;
- точки не должны дублироваться.
По координатам, использованным при построении рисунка, подготовим файл данных polygon.dat:
18 -10.812317 -18 10.812317 18 26.565051 -18 52.622632 54 52.622632 54 10.812317 18 -10.812317
Выполним скрипт в консоли:
$ python area.py polygon.dat
Вывод программы:
3.39532e+07
Поскольку большая полуось задавалась в километрах, результат получен в квадратных километрах.
Посмотрев на рисунок, легко заметить, что длины сторон нашего полигона сравнимы с радиусом сферы, и упомянутый выше эффект «провисания» линий может повлиять на точность вычисления площади.