Вычисление площади полигона на сфере и на эллипсоиде

Эта страница является черновиком статьи.

Одна-две фразы по существу.

Общие положения

Многоугольник на сфере

Определим полигон как простой многоугольник — участок поверхности, ограниченный замкнутой полилинией без самопересечений.

Полилиния в свою очередь — ломаная, образованная отрезками геодезических линий.

Геодезическая линия на плоскости — это прямая; геодезическая линия на сфере — дуга большой окружности.

Полный поворот контура

В общем случае определение площади многоугольника на искривлённой поверхности — нетривиальная задача. Нужно интегрировать по поверхности с пределами, заданными неявно. К счастью, математика может предложить обходные пути решения задачи.

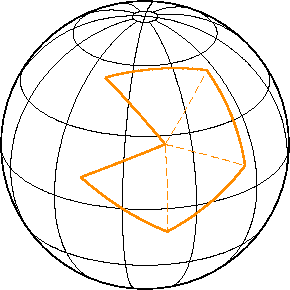
Представим себе точку, движущуюся вдоль контура полигона. Вершины являются точками поворота. Внутренний угол при вершине θ равен разности направлений α в предыдущую и следующую вершины, а поворот есть угол τ, смежный внутреннему:

${\begin{array}{rcl}\theta _{i}&=&\alpha _{i,i-1}-\alpha _{i,i+1}\\\tau _{i}&=&\pi -\theta _{i}\end{array}}$

На евклидовой плоскости, обойдя любой замкнутый контур без самопересечений, точка совершает поворот ровно на одну окружность — 360°, или 2π радиан. В случае многоугольника этот поворот складывается из суммы поворотов в вершинах.

На поверхности с ненулевой гауссовой кривизной общий поворот отличается от 2π на величину избытка или недостатка, пропорционального кривизне поверхности и площади фигуры.

Площадь полигона на сфере

Сферический избыток

В общем случае кривизна поверхности меняется в каждой точке, но не на сфере! Кривизна сферы постоянна, и площадь замкнутой фигуры однозначно соотносится с полным поворотом контура.

Отличие полного поворота от 2π радиан называется сферическим избытком ε, который пропорционален площади полигона S:

${\begin{array}{rcl}\varepsilon &=&2\pi -\displaystyle \sum _{i=1}^{n}\tau _{i}\\S&=&\varepsilon R^{2}\end{array}}$

где R — радиус сферы.

Алгоритм вычисления площади

Пусть n-угольник задан координатами вершин φ_i, λ_i, где φ_i — широта i-ой вершины, λ_i — долгота, i = 1, … , n.

1. Для каждой стороны из решения обратной геодезической задачи для её конечных вершин находим прямые и обратные азимуты α_{i, i+1} и α_{i+1, i}.
2. Для каждой вершины по азимутам α_{i, i−1} в предыдущую и α_{i, i+1} в последующую вершины находим поворот τ_i и добавляем его к полному повороту τ.
3. Вычисляем сферический избыток ε.
4. Вычисляем площадь полигона S.

Радиус сферы

Радиус сферы.

Ссылки

• Задачи на сфере: обратная геодезическая задача
• Earth radius