Вычисление площади полигона на сфере и на эллипсоиде

Эта страница является черновиком статьи.

Одна-две фразы по существу.

Общие положения

Многоугольник на сфере

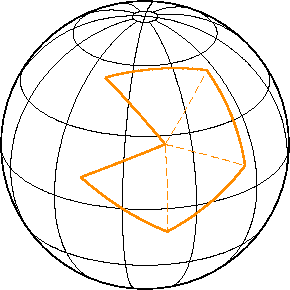
Определим полигон как простой многоугольник — участок поверхности, ограниченный замкнутой полилинией без самопересечений.

Полилиния в свою очередь — ломаная, образованная отрезками геодезических линий.

Геодезическая линия на плоскости — это прямая; геодезическая линия на сфере — дуга большой окружности.

Полный поворот контура

В общем случае определение площади многоугольника на искривлённой поверхности — нетривиальная задача. Нужно интегрировать по поверхности с пределами, заданными неявно. К счастью, математика может предложить обходные пути решения задачи.

Представим себе точку, движущуюся вдоль контура полигона. Вершины являются точками поворота. Внутренний угол при вершине θ равен разности направлений α в предыдущую и следующую вершины, а поворот есть угол τ, смежный внутреннему:

${\begin{array}{rcl}\theta _{i}&=&\alpha _{i,i-1}-\alpha _{i,i+1}\\\tau _{i}&=&\pi -\theta _{i}\end{array}}$

На евклидовой плоскости, обойдя любой замкнутый контур без самопересечений, точка совершает поворот ровно на одну окружность — 360°, или 2π радиан. В случае многоугольника этот поворот складывается из суммы поворотов в вершинах.

На поверхности с ненулевой гауссовой кривизной общий поворот отличается от 2π на величину избытка или недостатка, пропорционального кривизне поверхности и площади фигуры.

Площадь полигона на сфере

Сферический избыток

В общем случае кривизна поверхности меняется в каждой точке, но не на сфере! Кривизна сферы постоянна, и площадь замкнутой фигуры легко определяется по полному повороту контура.

Отличие полного поворота от 2π радиан называется сферическим избытком ε, который пропорционален площади полигона S:

${\begin{array}{rcl}\varepsilon &=&2\pi -\displaystyle \sum _{i=1}^{n}\tau _{i}\\S&=&\varepsilon R^{2}\end{array}}$

где R — радиус сферы.

Ссылки

• Задачи на сфере: обратная геодезическая задача