TIN&SQL: различия между версиями
Trir (обсуждение | вклад) Нет описания правки |
Trir (обсуждение | вклад) (→Рёбра) |
||
| (не показано 29 промежуточных версий этого же участника) | |||
| Строка 7: | Строка 7: | ||
==Структура данных== | ==Структура данных== | ||
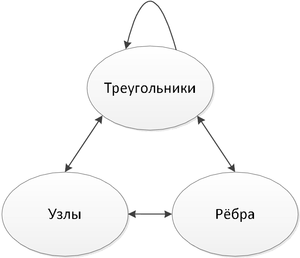
Структура данных для TIN определяет скорость и удобство работы. В триангуляции можно выделить 3 основных вида объектов: узлы (точки, вершины), рёбра (отрезки) и треугольники. | Структура данных для TIN определяет скорость и удобство работы. В триангуляции можно выделить 3 основных вида объектов: узлы (точки, вершины), рёбра (отрезки) и треугольники. | ||
<br /> | |||
[[Файл:Pic1.png|thumb|right|300px|Рис. 1. Связи между объектами TIN]] | |||
:Возможны следующие структуры данных: | :Возможны следующие структуры данных: | ||
#«Узлы с соседями» | #«Узлы с соседями» | ||
| Строка 13: | Строка 15: | ||
#«Узлы, рёбра и треугольники» | #«Узлы, рёбра и треугольники» | ||
#«Узлы, простые рёбра и треугольники» | #«Узлы, простые рёбра и треугольники» | ||
<br /> | <br /> | ||
:СД влияет на два важных момента: | :СД влияет на два важных момента: | ||
| Строка 21: | Строка 21: | ||
<br /> | <br /> | ||
Для поиска лучше п.4 и 5 - так, как существует 3 таблицы и можно искать во всех направлениях. А п. 1 и 2 - лучше для изменений, так нужно минимальное количество действий. Оптимальным для поиска и изменений является п. 3. | Для поиска лучше п.4 и 5 - так, как существует 3 таблицы и можно искать во всех направлениях. А п. 1 и 2 - лучше для изменений, так нужно минимальное количество действий. Оптимальным для поиска и изменений является п. 3. | ||
<br /> | |||
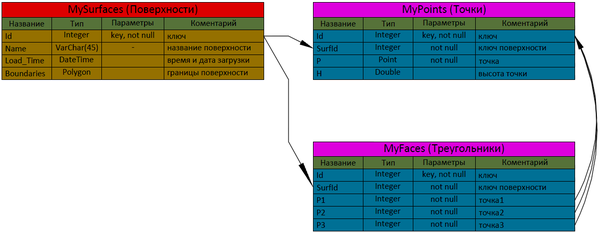
Требуется хранить множество поверхностей - по этому будет таблица MySurfaces, а также таблицы MyPoints и MyFaces. Конечно требуются 3D точки, но в MySQL реализованы только 2D точки, по этому, высоту придётся хранить отдельно. В MyFaces будем хранить только указатели на точки. | |||
[[Файл:Tin_sql_Pic2_v01.png|thumb|left|600px|Рис. 2. Базовая структура БД]] | |||
<br clear="all"/> | |||
В данной структуре нет явного описания рёбер и связей между треугольниками. | |||
{{Скрытый | |||
|Рамка = 1px dashed #aa0000 | |||
|Ссылка = left | |||
|Выравнивание_заголовка = left | |||
|Заголовок = Структура таблиц | |||
|Фон_заголовка = #ccccff | |||
|Содержание = | |||
<syntaxhighlight lang="SQL"> | |||
CREATE TABLE `mysurfaces` ( | |||
`id` int(11) unsigned NOT NULL AUTO_INCREMENT, | |||
`sname` varchar(45) DEFAULT NULL, | |||
`Load_Time` datetime DEFAULT CURRENT_TIMESTAMP, | |||
`boundres` polygon DEFAULT NULL, | |||
PRIMARY KEY (`id`) | |||
) ENGINE=MyISAM DEFAULT CHARSET=utf8; | |||
CREATE TABLE `mypoints` ( | |||
`idMyPoints` int(10) unsigned NOT NULL AUTO_INCREMENT, | |||
`MyPointscol` point NOT NULL, | |||
`H` double DEFAULT NULL, | |||
`SurfID` int(10) unsigned NOT NULL, | |||
PRIMARY KEY (`idMyPoints`), | |||
SPATIAL KEY `spi_p` (`MyPointscol`) | |||
) ENGINE=MyISAM DEFAULT CHARSET=utf8; | |||
CREATE TABLE `myfaces` ( | |||
`id` int(10) unsigned NOT NULL AUTO_INCREMENT, | |||
`p1` int(10) unsigned NOT NULL, | |||
`p2` int(10) unsigned NOT NULL, | |||
`p3` int(10) unsigned NOT NULL, | |||
`SurfID` int(10) unsigned NOT NULL, | |||
PRIMARY KEY (`id`) | |||
) ENGINE=MyISAM DEFAULT CHARSET=utf8; | |||
</syntaxhighlight>}} | |||
==Рёбра== | |||
Нужно получить рёбра. Для этого сделаем три представления: | |||
<br /> | |||
1. Извлечём рёбра из треугольников (wq_Ribs1) | |||
<math>p1, ~ p2, ~ p3 \Rightarrow \begin{matrix} p1, ~ p2 \\ p2, ~ p3 \\ p3, ~ p1 \end{matrix}</math> | |||
<br /> | |||
Мы получаем двойной набор рёбер – в обе стороны (не считая крайних) | |||
{{Скрытый | |||
|Рамка = 1px dashed #aa0000 | |||
|Ссылка = left | |||
|Выравнивание_заголовка = left | |||
|Заголовок = wq_Ribs1 | |||
|Фон_заголовка = #ccccff | |||
|Содержание = | |||
<syntaxhighlight lang="SQL"> | |||
select `myfaces`.`id` AS `id`,`myfaces`.`p1` AS `p1`,`myfaces`.`p2` AS `p2`,`myfaces`.`SurfID` AS `SurfID` from `myfaces` | |||
union | |||
select `myfaces`.`id` AS `id`,`myfaces`.`p2` AS `p1`,`myfaces`.`p3` AS `p2`,`myfaces`.`SurfID` AS `SurfID` from `myfaces` | |||
union | |||
select `myfaces`.`id` AS `id`,`myfaces`.`p3` AS `p1`,`myfaces`.`p1` AS `p2`,`myfaces`.`SurfID` AS `SurfID` from `myfaces`; | |||
</syntaxhighlight>}} | |||
2. Получить ссылки на треугольники (wq_Ribs2) | |||
<br /> | |||
<math>p1, ~ p2 \Rightarrow p1, ~ p2, ~ t1 , ~ t2 </math> | |||
<br /> | |||
Объединяем преведущую таблицу с самой собой – по симметричным рёбрам и получаем оба треугольника | |||
{{Скрытый | |||
|Рамка = 1px dashed #aa0000 | |||
|Ссылка = left | |||
|Выравнивание_заголовка = left | |||
|Заголовок = wq_Ribs2 | |||
|Фон_заголовка = #ccccff | |||
|Содержание = | |||
<syntaxhighlight lang="SQL"> | |||
select `tbl1`.`SurfID` AS `SurfID`,`tbl1`.`id` AS `t1`,`tbl2`.`id` AS `t2`,`tbl1`.`p1` AS `p1`,`tbl1`.`p2` AS `p2` | |||
from (`allmyribs` `tbl1` left join `allmyribs` `tbl2` on(((`tbl1`.`p1` = `tbl2`.`p2`) and (`tbl1`.`p2` = `tbl2`.`p1`)))); | |||
</syntaxhighlight>}} | |||
3. Сортируем ключи слева на право, и удаляем дубликаты (wq_Ribs3) | |||
<math>\begin{matrix} p1, ~ p2 \\ p2, ~ p1 \\ p2, ~ p3 \\ p3, ~ p2 \\ p3, ~ p1 \end{matrix} \Rightarrow \begin{matrix} p1, ~ p2 \\ p2, ~ p3 \\ p1, ~ p3 \end{matrix}</math> | |||
{{Скрытый | |||
|Рамка = 1px dashed #aa0000 | |||
|Ссылка = left | |||
|Выравнивание_заголовка = left | |||
|Заголовок = wq_Ribs3 | |||
|Фон_заголовка = #ccccff | |||
|Содержание = | |||
<syntaxhighlight lang="SQL"> | |||
select distinct `allmyribs_tri`.`SurfID` AS `SurfID`, | |||
if((`allmyribs_tri`.`p2` < `allmyribs_tri`.`p1`),`allmyribs_tri`.`p2`,`allmyribs_tri`.`p1`) AS `p1`, | |||
if((`allmyribs_tri`.`p2` < `allmyribs_tri`.`p1`),`allmyribs_tri`.`p1`,`allmyribs_tri`.`p2`) AS `p2`, | |||
if((`allmyribs_tri`.`t2` < `allmyribs_tri`.`t1`),`allmyribs_tri`.`t2`,`allmyribs_tri`.`t1`) AS `t1`, | |||
if((`allmyribs_tri`.`t2` < `allmyribs_tri`.`t1`),`allmyribs_tri`.`t1`,`allmyribs_tri`.`t2`) AS `t2` | |||
from `allmyribs_tri`; | |||
</syntaxhighlight>}} | |||
==Ссылки== | ==Ссылки== | ||
Текущая версия от 21:25, 11 января 2014
Введение
TIN (Triangulated Irregular Network) - Нерегулярная сеть триангуляции, структура данных используемая в ГИС для представления поверхности. Фактически является векторным представлением, её растровым аналогом является DEM (Digital Elevation Model - Цифровая модель высот). TIN основана на Триангуляции Делоне, но не тождественна её, так как последняя является более строгим понятием. TIN состоит из непересекающихся треугольников - это накладывает определённые ограничения (не может быть "пещер" и с вертикальными стенками - тоже беда) и фактически означает, что TIN имеет размерность 2.5D (x, y и z)
Удобство использования TIN заключается в возможности иметь разное "разрешение" для участков с разной сложностью.
В стандарте "Simple feature access" существует возможность хранения TIN, но фактически такая возможность существует только в Oracle Spatial и то - не по стандарту. Также существует потребность обращаться к отдельным элементам TIN. Далее рассмотрим вариант хранения TIN в MySQL.
Структура данных
Структура данных для TIN определяет скорость и удобство работы. В триангуляции можно выделить 3 основных вида объектов: узлы (точки, вершины), рёбра (отрезки) и треугольники.
- Возможны следующие структуры данных:
- «Узлы с соседями»
- «Двойные рёбра»
- «Узлы и треугольники»
- «Узлы, рёбра и треугольники»
- «Узлы, простые рёбра и треугольники»
- СД влияет на два важных момента:
- Поиск нужного объекта
- Внесение изменений и добавления новых объектов
Для поиска лучше п.4 и 5 - так, как существует 3 таблицы и можно искать во всех направлениях. А п. 1 и 2 - лучше для изменений, так нужно минимальное количество действий. Оптимальным для поиска и изменений является п. 3.
Требуется хранить множество поверхностей - по этому будет таблица MySurfaces, а также таблицы MyPoints и MyFaces. Конечно требуются 3D точки, но в MySQL реализованы только 2D точки, по этому, высоту придётся хранить отдельно. В MyFaces будем хранить только указатели на точки.
В данной структуре нет явного описания рёбер и связей между треугольниками.
Рёбра
Нужно получить рёбра. Для этого сделаем три представления:
1. Извлечём рёбра из треугольников (wq_Ribs1)
Мы получаем двойной набор рёбер – в обе стороны (не считая крайних)
2. Получить ссылки на треугольники (wq_Ribs2)
Объединяем преведущую таблицу с самой собой – по симметричным рёбрам и получаем оба треугольника
3. Сортируем ключи слева на право, и удаляем дубликаты (wq_Ribs3)